视觉SLAM十四讲学习笔记（四）

---

李群与李代数

李群与李代数基础

SO(3)和SE(3)对乘法运算构成群
封闭性：代数系
结合律：半群
幺元：幺半群
逆：群

李群

李群是具有连续（光滑）性质的群。

李代数的引出

$$R{R}^T=I$$
两段求导得
$$\dot{R}(t)R(t{)}^T=-(\dot{R}(t)R(t{)}^T{)}^T$$
可得$\dot{R}(t)R(t{)}^T$是反对称矩阵
定义$A^{\vee }=a,s.t.a^{\wedge }=A$
进而有
$$\dot{R}(t)R(t{)}^T=\varphi (t{)}^{\wedge }$$
等式两边右乘R(t)，可得
$$\dot{R}(t)=\varphi (t{)}^{\wedge }R(t)$$
考虑$t_0=0,R(0)=I$，有
$$\begin{array}{rl}R(t)& \approx R(t_0)+\dot{R}(t_0)(t-t_0)\\ & =I+\varphi (t_0{)}^{\wedge }t\end{array}$$
在$t_0$附近，设$\varphi$保持为常数$\varphi (t0)={\varphi }_0$
则有
$$\dot{R}(t)={\varphi }_0^{\wedge }R(t)$$
解得
$$R(t)=\exp ({\varphi }_0^{\wedge }t)$$

李代数的定义

李代数由一个集合V、一个数域F和一个二元运算组成。
满足如下性质：

1. 封闭性
2. 双线性
3. 自反性
4. 雅可比等价

其中二元运算被称为李括号

李代数$\mathfrak{s}\mathfrak{o}$(3)

两个向量${\varphi }_1,{\varphi }_2$的李括号为
$$[{\varphi }_1,{\varphi }_2]=({\Phi }_1{\Phi }_2-{\Phi }_2{\Phi }_1{)}^{\vee }$$
s o ( 3 ) = { ϕ ∈ R 3 , Φ = ϕ ∧ ∈ R 3 × 3 } \mathfrak{so}(3)=\{\phi\in\R^3,\Phi=\phi^{\wedge}\in\R^{3\times 3}\} so(3)={ϕ∈R3,Φ=ϕ∧∈R3×3}
$$R=\exp ({\varphi }^{\wedge })$$

李代数$\mathfrak{s}\mathfrak{e}$(3)

s e ( 3 ) = { ξ = [ ρ ϕ ] ∈ R 6 , ρ ∈ R 3 , ϕ ∈ s o ( 3 ) , ξ ∧ = [ ϕ ∧ ρ 0 T 0 ] ∈ R 4 × 4 } \mathfrak{se}(3)=\{\xi=\begin{bmatrix}\rho\\\phi\end{bmatrix} \in\R^6,\rho\in\R^3,\phi\in \mathfrak{so}(3),\xi^{\wedge}= \begin{bmatrix}\phi^{\wedge} && \rho \\ 0^T && 0\end{bmatrix}\in\R^{4\times 4}\} se(3)={ξ=[ρϕ​]∈R6,ρ∈R3,ϕ∈so(3),ξ∧=[ϕ∧0T​​ρ0​]∈R4×4}
前三维为平移（含义与变换矩阵中的平移不同）
后三维为旋转，是so(3)元素

扩展^符号的含义

se(3)中，使用^符号，将一个六维向量转换成四维矩阵

4.2 指数与对数映射

SO(3)上的指数映射

将$\varphi$表示为$\theta a$
对于$a^{\bigwedge }$，有两条性质
可得：

即罗德里格斯公式，这表明指数映射将$\mathfrak{s}\mathfrak{o}(3)$中的向量映射为了SO(3)中的旋转矩阵。
逆运算为对数映射：
用上文中迹的性质由R计算$\theta$和$a$更加方便。
固定旋转角度在$\pm \pi$之间时，指数运算是一个双射。

se(3)上的指数映射

定义$J=\sum _{n=0}^{\infty }\frac{1}{(n+1)!}({\varphi }^{\wedge }{)}^n$

根据变换矩阵求se(3)上的对应向量

从左上角的R计算旋转向量，而t满足：
$$t=J\rho$$

总结

李代数求导与扰动模型

BCH公式：
相比标量，两个矩阵的指数之积会产生余项

忽略小量

考虑SO(3)上的李代数$\ln (\exp ({\varphi }_1{)}^{\wedge }\exp ({\varphi }_2{)}^{\wedge }{)}^{\vee }$
${\varphi }_1或{\varphi }_2$为小量时，可忽略二次以上的项，即

左乘模型：

右乘模型：
可整理为：
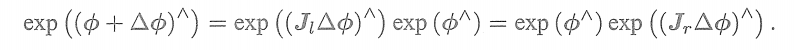对于se(3)，由类似的近似
### SO(3)上的李代数求导
$$z=Tp+w$$
存在误差
$$e=z-Tp$$
目标函数

李代数求导

扰动模型（左乘）

SE(3)上的李代数求导

前几步与SO(3)上的扰动模型类似，后几步由于^符号的定义不同而略有不同：

$\odot$算符：
求导顺序规则：

相似变换群与李代数

问题：如果在单目SLAM中使用SE(3)来表示位姿，那么由于尺度不确定性与尺度漂移，整个SLAM过程中的尺度会发生变化，这在SE(3)中未能体现出来。

解决方法：对于位于空间的点p，在相机坐标系下要经过一个相似变换，而非欧氏变换：

尺度s同时作用在p的3个坐标之上，对p进行了一次缩放。

相似变换群

Sim(3)的李代数

$\mathfrak{s}\mathfrak{i}\mathfrak{m}(3)$元素是一个7维向量$\zeta$。它的前6维与$\mathfrak{s}\mathfrak{e}(3)$相同，最后多了一项$\sigma$。

指数映射

李代数与李群的对应关系

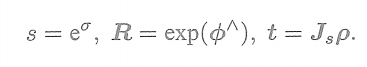
BCH近似

给出扰动模型的结果：
设给予$Sp$左侧一个小扰动$\exp ({\zeta }^{\wedge })$，并求$Sp$对于扰动的导数。因为$Sp$是4维的齐次坐标，$\zeta$是7维向量，所以该导数应该是4x7的雅可比。方便起见，记$Sp$的前3维组成向量为q，那么：