算法复杂度

爱吃糖的猫

已于 2023-07-14 16:52:33 修改

阅读量164

点赞数

分类专栏：算法文章标签：算法数据结构

于 2023-06-15 15:20:44 首次发布

本文链接：https://blog.youkuaiyun.com/weixin_42745647/article/details/131228750

版权

算法专栏收录该内容

3 篇文章

订阅专栏

本文介绍了算法的时间复杂度和空间复杂度，包括递归算法的复杂度计算方法。时间复杂度关注计算操作数量，区分了常数级O(1)、对数阶O(logN)、线性阶O(N)、线性对数O(NlogN)、平方阶O(N^2)和指数阶O(2^N)。空间复杂度则涉及指令空间、数据空间和栈帧空间，分析了不同数据结构和递归情况下的空间占用。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

本文节选自我的博客：算法复杂度

💖 作者简介：大家好，我是MilesChen，偏前端的全栈开发者。
📝 优快云主页：爱吃糖的猫🔥
📣 我的博客：爱吃糖的猫
📚 Github主页: MilesChen
🎉 支持我：点赞👍+收藏⭐️+留言📝
💬介绍：The mixture of WEB+DeepLearning+Iot+anything🍁

递归算法时间复杂度 = 递归的次数 * 每次递归中的操作次数
递归算法的空间复杂度 = 每次递归的空间复杂度 * 递归深度

时间复杂度

统计的是算法的「计算操作数量」，而不是「运行的绝对时间」。计算操作数量和运行绝对时间呈正相关关系，并不相等。算法运行时间受到「编程语言、计算机处理器速度、运行环境」等多种因素影响。例如，同样的算法使用 Python 或 C++ 实现、使用 CPU 或 GPU 、使用本地 IDE 或力扣平台提交，运行时间都不同。
体现的是计算操作随数据大小 N 变化时的变化情况。假设算法运行总共需要「 1 次操作」、「 100次操作」，此两情况的时间复杂度都为常数级 O(1) ；需要「 N 次操作」、「 100N 次操作」的时间复杂度都为O(N) 。

时间复杂度具有「最差」、「平均」、「最佳」三种情况，分别使用（欧米可容）O , （西塔）Θ , （欧米茄）Ω 三种符号表示。

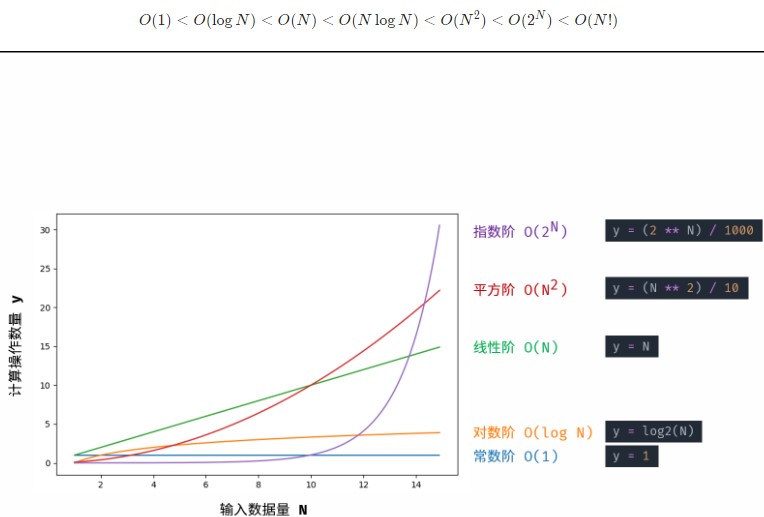
复杂度只与N有关
O（1）：运行次数与 N大小呈常数关系，即不随输入数据大小 N 的变化而变化
O（logN）: 对数阶，对数阶常出现于「二分法」、「分治」等算法中，体现着 “一分为二” 或 “一分为多” 的算法思想。

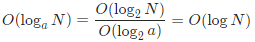
O（N）：循环运行次数与 N 大小呈线性关系，注意：即使有一层循环a，这样的与N无关的循环，也是O（N）
O（NlogN）: 线性对数，两层循环相互独立，第一层和第二层时间复杂度分别为O（logN）和 O（N），如
「快速排序」、「归并排序」、「堆排序」
O（N^{2）：冒泡排序，第一层为O（N），第二层为O（N/2），[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-JIcySgGZ-1686813594312)(算法复杂度_files/0b5bc695-339c-4ff2-9b31-46f500511f79.png)]，所以冒泡是O（N}2）
O（2^N）: 指数阶,递归操作，1-2-4-8.函数中两次递归，如果函数中三次递归应该是O（3^N）
O（N！）：全排列问题，阶乘常使用递归实现，算法原理：第一层分裂出 N 个，第二层分裂出 N - 1 个，…… ，直至到第 N 层时终止并回溯

def algorithm(N):
    if N <= 0: return 1
    count = 0
    for _ in range(N):
        count += algorithm(N - 1)
    return count

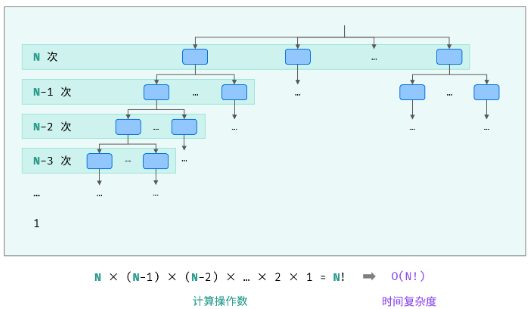
空间复杂度

指令空间:编译后，程序指令所使用的内存空间。
数据空间：算法中的各项变量使用的空间，包括：声明的常量、变量、动态数组、动态对象等使用的内存空间。

class Node:
    def __init__(self, val):
        self.val = val
        self.next = None
def algorithm(N):
    num = N         # 变量
    nums = [0] * N  # 动态数组
    node = Node(N)  # 动态对象

栈帧空间：

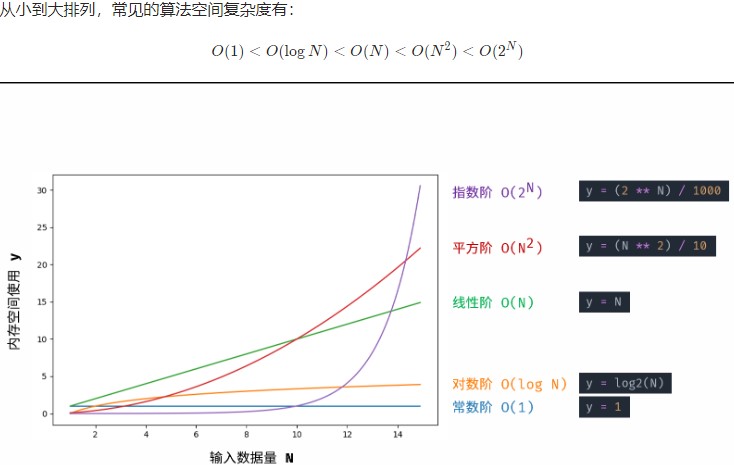
O（1）：普通常量、变量、对象、元素数量与输入数据大小 NN 无关的集合，皆使用常数大小的空间。

O（logN）: 对数阶常出现于分治算法的栈帧空间累计、数据类型转换等

O（N）：元素数量与 N 呈线性关系的任意类型集合（常见于一维数组、链表、哈希表等）、单层递归，皆使用线性大小的空间。
O（N^2）：元素数量与 NN 呈平方关系的任意类型集合（常见于矩阵），皆使用平方大小的空间。

def algorithm(N):
    num_matrix = [[0 for j in range(N)] for i in range(N)]
    node_matrix = [[Node(j) for j in range(N)] for i in range(N)]

递归调用时同时存在 N 个未返回的 algorithm() 函数，使用 O(N) 栈帧空间；每层递归函数中声明了数组，平均长度为N/2 ，使用O(N) 空间；因此总体空间复杂度为 O(N ^2 ) 。

def algorithm(N):
    if N <= 0: return 0
    nums = [0] * N
    return algorithm(N - 1)

O（2^N）:

复杂度速查表

有任何疑问和想法，欢迎在评论区与我交流。