js解leetcode(62)-中等

1.推多米诺

题目：

一行中有 N 张多米诺骨牌，我们将每张多米诺骨牌垂直竖立。

在开始时，我们同时把一些多米诺骨牌向左或向右推。

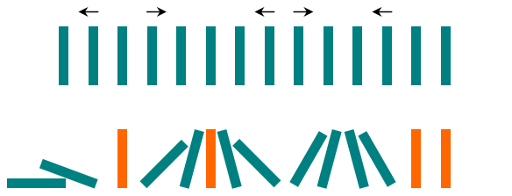
每过一秒，倒向左边的多米诺骨牌会推动其左侧相邻的多米诺骨牌。

同样地，倒向右边的多米诺骨牌也会推动竖立在其右侧的相邻多米诺骨牌。

如果同时有多米诺骨牌落在一张垂直竖立的多米诺骨牌的两边，由于受力平衡， 该骨牌仍然保持不变。

就这个问题而言，我们会认为正在下降的多米诺骨牌不会对其它正在下降或已经下降的多米诺骨牌施加额外的力。

给定表示初始状态的字符串 "S" 。如果第 i 张多米诺骨牌被推向左边，则 S[i] = 'L'；如果第 i 张多米诺骨牌被推向右边，则 S[i] = 'R'；如果第 i 张多米诺骨牌没有被推动，则 S[i] = '.'。

返回表示最终状态的字符串。

思路：用栈stack存储临时的字符串。

遍历字符串时，记录上一次出现的L或者R。如果上一次出现的是L，那么当前的点就是点，将点.推入stack。如果上一次出现的是R，那么当前的点就有可能是R，所以此时将字符串R推入stack

遇到R时，R对左侧的字符串没有影响，栈内储存的字符串不变，所以将栈内的字符串直接拼接；

遇到L时，如果上一次遇到的不是R，那么左侧将全部变为L，

如果上一次遇到的是R，那么栈内的字符就是各一半是R和L。

时间复杂度O(n)，空间复杂度O(n)

var pushDominoes = function(dominoes) {
  let flag = "";
  let temp = [];
  let res = "";
  for (const s of dominoes) {
    if (s === ".") {
      temp.push(flag === "R" ? "R" : ".");
    } else if (s === "R") {
      res += temp.join("");
      temp = [];
      flag = "R";
      res += "R";
    } else {
      if (flag !== "R") {
        res += temp.fill("L").join("");
      } else {
        const l = temp.length;
        res += `${new Array(~~(l / 2)).fill("R").join("")}${
          l % 2 ? "." : ""
        }${new Array(~~(l / 2)).fill("L").join("")}`;
      }
      temp = [];
      res += "L";
      flag = "L";
    }
  }
  res += temp.join("");
  return res;
};

2.钥匙和房间

题目：

有 N 个房间，开始时你位于 0 号房间。每个房间有不同的号码：0，1，2，...，N-1，并且房间里可能有一些钥匙能使你进入下一个房间。

在形式上，对于每个房间 i 都有一个钥匙列表 rooms[i]，每个钥匙 rooms[i][j] 由 [0,1，...，N-1] 中的一个整数表示，其中 N = rooms.length。 钥匙 rooms[i][j] = v 可以打开编号为 v 的房间。

最初，除 0 号房间外的其余所有房间都被锁住。

你可以自由地在房间之间来回走动。

如果能进入每个房间返回 true，否则返回 false。

思路：这是一个典型的dfs或者bfs。初始化矩阵dp。dp[i]表示这个房间能否被打开，默认是false，即不能打开。再得到某个房间的钥匙时，可以打开这个房间，即对应的dp[i]设为true，然后找到这个打开的房间的钥匙，进行一次循环操作。为了避免死循环，遇到打开的房间时，应该停止这轮遍历

时间复杂度O(n)，空间复杂度O(n)

/**
 * @param {number[][]} rooms
 * @return {boolean}
 */
var canVisitAllRooms = function(rooms) {
  const l = rooms.length;
  const dp = new Array(l).fill(false);
  const dfs = (i) => {
    if (dp[i]) return;
    dp[i] = true;
    const next = rooms[i];
    next.forEach((item) => {
      dfs(item);
    });
  };
  dfs(0);
  return dp.every((item) => item);
};

3.将数组拆分成斐波那契数列

题目：

给定一个数字字符串 S，比如 S = "123456579"，我们可以将它分成斐波那契式的序列 [123, 456, 579]。

形式上，斐波那契式序列是一个非负整数列表 F，且满足：

• 0 <= F[i] <= 2^31 - 1，（也就是说，每个整数都符合 32 位有符号整数类型）；
• F.length >= 3；
• 对于所有的0 <= i < F.length - 2，都有 F[i] + F[i+1] = F[i+2] 成立。

另外，请注意，将字符串拆分成小块时，每个块的数字一定不要以零开头，除非这个块是数字 0 本身。

返回从 S 拆分出来的任意一组斐波那契式的序列块，如果不能拆分则返回 []。

思路：

斐波那契序列：第3项 = 前2项和。prev存前2项。

r为结果集 枚举：从0到i，i < 字符串长度，每次i + 1 prev满2项。2项和=当前数，prev[0]放r，prev[0]=prev[1], prev[1]=当前数 指针+1，递归 新prev 与 后数 比较 指针=字符串长度，找到一解，prev放r，标记end为true（找多解不标记）

回溯：指针到不了末尾。之前放r的数无解，从r弹出该数 prev<2项 且 指针!=最后字符（=放不满3项） prev放当前数，指针+1，递归 回溯：指针到不了末尾 当前数是0，后数不能以0开头，终止循环 end为true，已找到一解，终止循环 之前放prev的数无解，从prev弹出该数

/**
 * @param {string} S
 * @return {number[]}
 */
var splitIntoFibonacci = function(S, start = 0, r = []) {
    if (start === S.length) return r.end = true
    for (var i = start, cur = 0; i < S.length; i++) {
        cur = cur * 10 + (S[i] | 0)
        if (cur > Math.pow(2, 31) - 1) break
        if (r.length > 1) {
            if (r[r.length - 2] + r[r.length - 1] === cur) {
                r.push(cur)
                if (splitIntoFibonacci(S, i + 1, r) === true) return true
                r.pop()
            }
        } else if (i < S.length - 1) {
            r.push(cur)
            if (splitIntoFibonacci(S, i + 1, r) === true || r.end) break
            r.pop()
            if (cur === 0) break
        }
    }
    return r
};

4.数组中最长的山脉

题目：

我们把数组 A 中符合下列属性的任意连续子数组 B 称为 “山脉”：

• B.length >= 3
• 存在 0 < i < B.length - 1 使得 B[0] < B[1] < ... B[i-1] < B[i] > B[i+1] > ... > B[B.length - 1]

（注意：B 可以是 A 的任意子数组，包括整个数组 A。）

给出一个整数数组 A，返回最长 “山脉” 的长度。

如果不含有 “山脉” 则返回 0。、

思路：动态规划。初始化两个数组dp1和dp2，dp1记录以每个元素为终点的连续递增子数组的长度，dp2记录以每个元素为起点的连续递减子数组的长度，所以对于任意一个元素i，以它为顶点的山脉长度是dp1[i]+dp2[i]-1。注意过滤一下dp1和dp2中长度小于2的元素，因为这时不能组成山脉

时间复杂度O(n)，空间复杂度O(n)

/**
 * @param {number[]} arr
 * @return {number}
 */
var longestMountain = function(arr) {
  const l = arr.length;
  const dp1 = new Array(l).fill(1);
  const dp2 = new Array(l).fill(1);
  for (let i = 0; i < l - 1; i++) {
    if (arr[i] < arr[i + 1]) {
      dp1[i + 1] = dp1[i] + 1;
    }
  }
  for (let i = l - 1; i > 0; i--) {
    if (arr[i] < arr[i - 1]) {
      dp2[i - 1] = dp2[i] + 1;
    }
  }
  const res = dp1
    .map((i, index) => [i, index])
    .filter((item) => item[0] > 1 && dp2[item[1]] > 1)
    .map((item) => item[0] + dp2[item[1]]);
  return res.length ? Math.max(...res) - 1 : 0;
};

5.一手顺子

题目：

爱丽丝有一手（hand）由整数数组给定的牌。 

现在她想把牌重新排列成组，使得每个组的大小都是 W，且由 W 张连续的牌组成。

如果她可以完成分组就返回 true，否则返回 false。

思路：用map记录数组每个元素及出现的次数。

在每一轮执行次数为W的循环中，先从map中取出最小的数作为当前的数pre，然后依次判断pre+1是否在map中，如果存在且次数大于1，map中pre+1的值-1，如果存在且次数等于1，map删除pre的key；如果不存在，直接返回false

/**
 * @param {number[]} hand
 * @param {number} W
 * @return {boolean}
 */
var isNStraightHand = function(hand, W) {
  const l = hand.length;
  const map = new Map();
  for (const n of hand) {
    map.set(n, (map.get(n) || 0) + 1);
  }
  hand.sort((a, b) => a - b);
  const handlMap = (v) => {
    if (map.get(v) > 1) {
      map.set(v, map.get(v) - 1);
    } else {
      map.delete(v);
    }
  };
  if (l % W) return false;
  if (W === 1) return true;
  while (map.size) {
    let pre = Math.min(...map.keys());
    let c = W;
    handlMap(pre);
    while (--c) {
      if (!map.get(pre + 1)) return false;
      handlMap(pre + 1);
      pre++;
    }
  }
  return true;
};