蚁群算法(ACO)

简介

蚁群算法(ant colony optimization, ACO)，是一种用来在图中寻找优化路径的机率型算法。其灵感来源于蚂蚁在寻找食物过程中发现路径的行为。

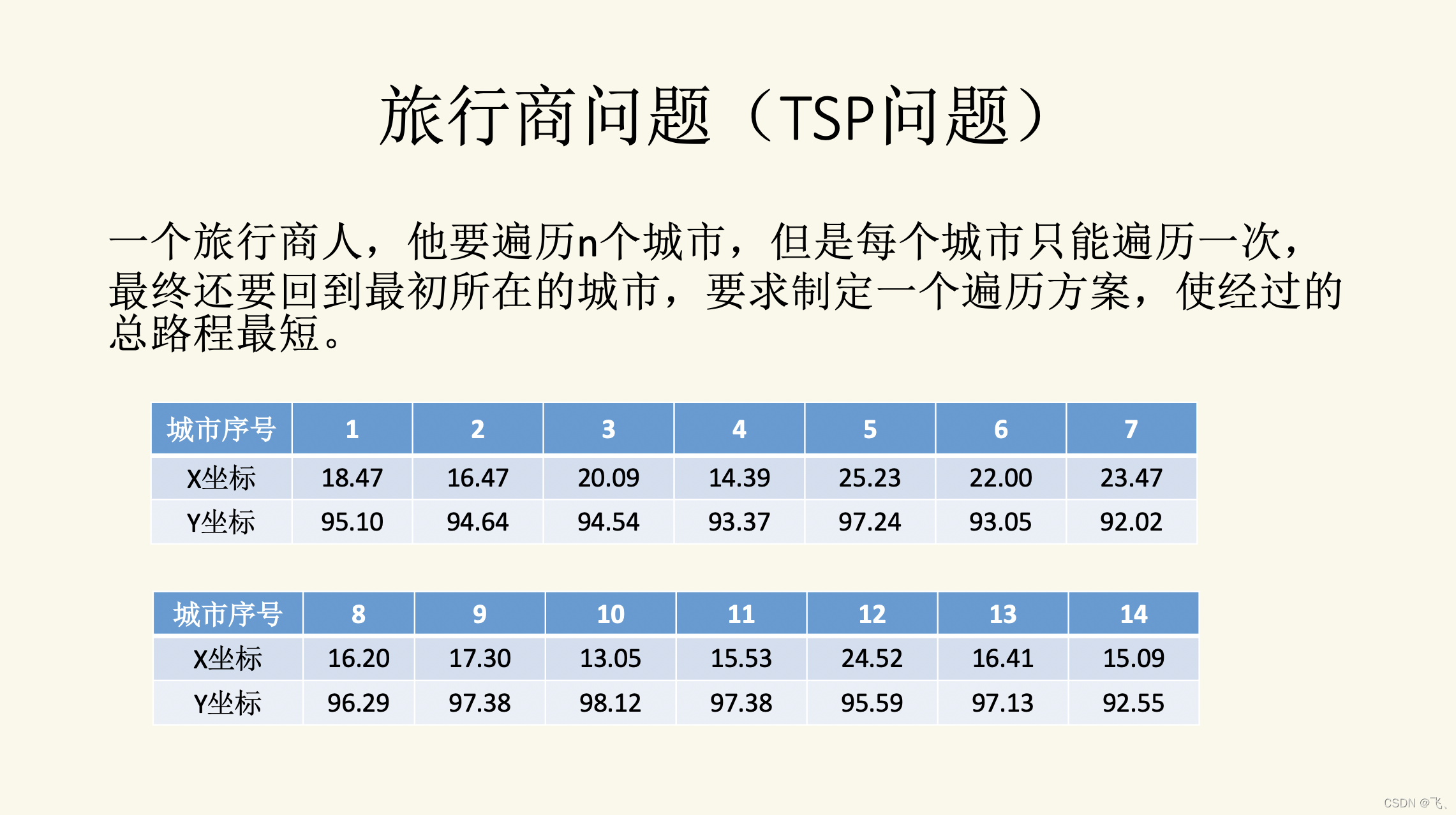
它能够求出从原点出发，经过若干个给定的需求点，最终返回原点的最短路径。这也就是著名的旅行商问题(Traveling Saleman Problem，TSP)。

蚁群算法是一种模拟进化算法。

基本原理

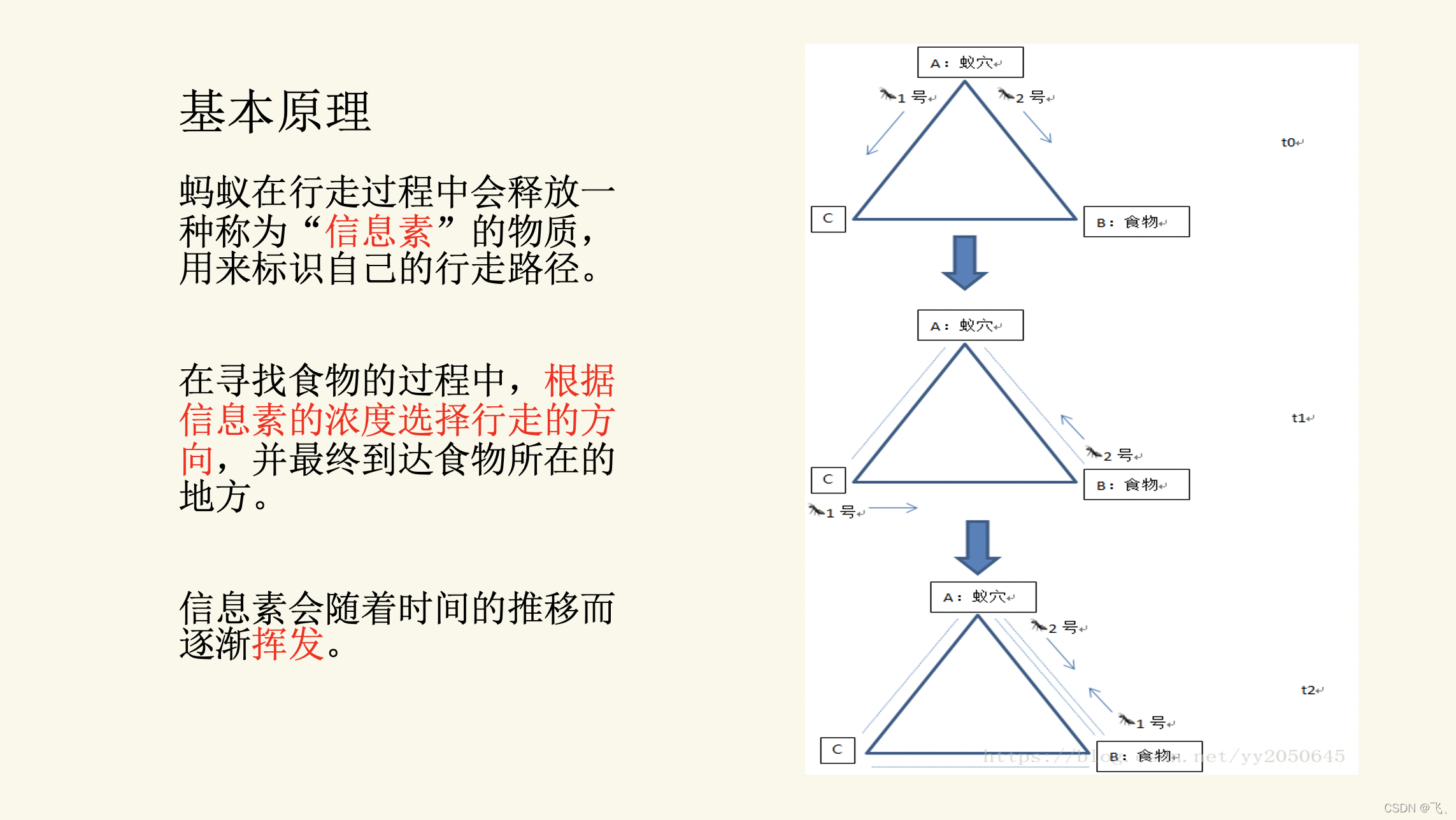
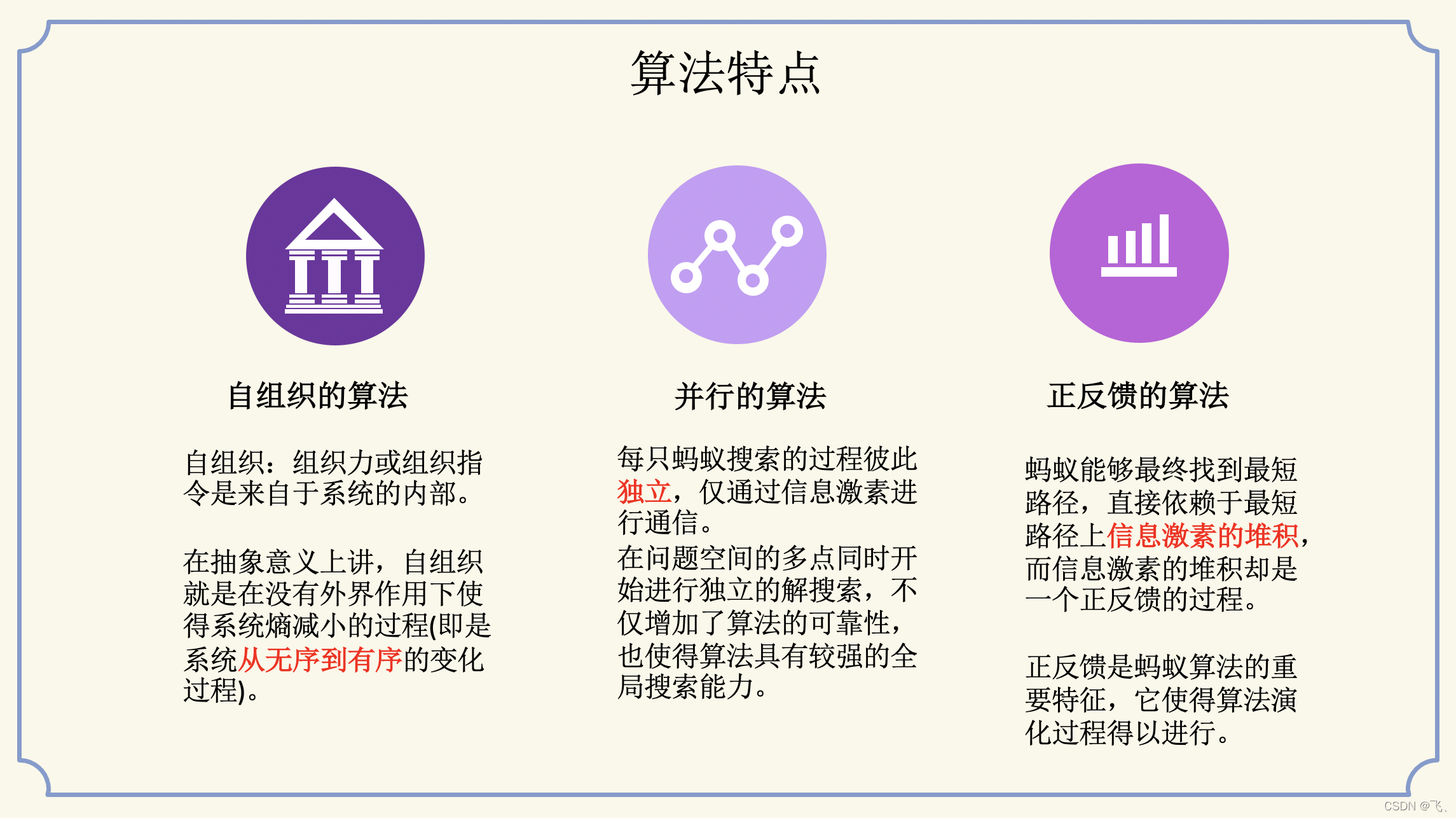
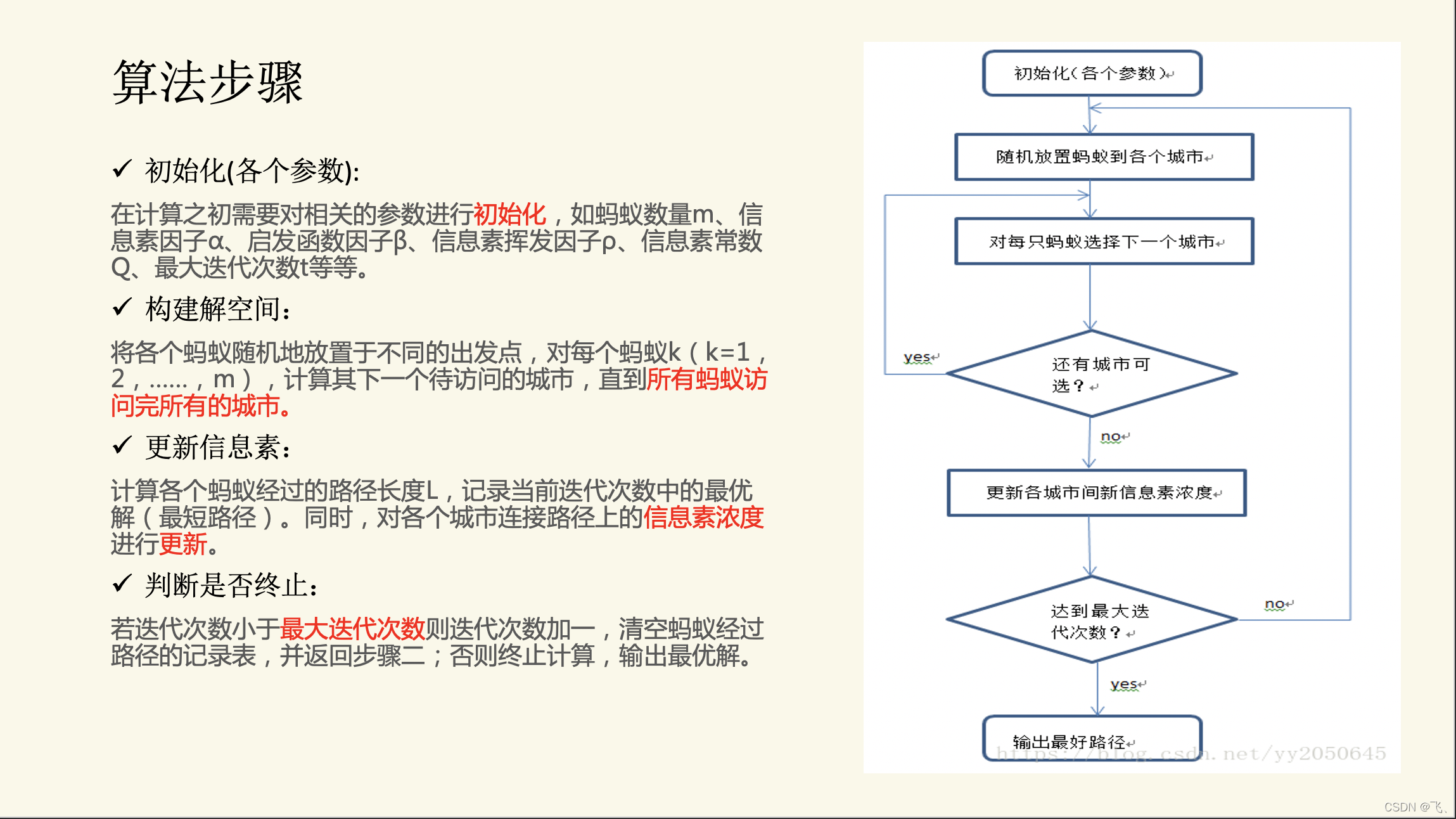
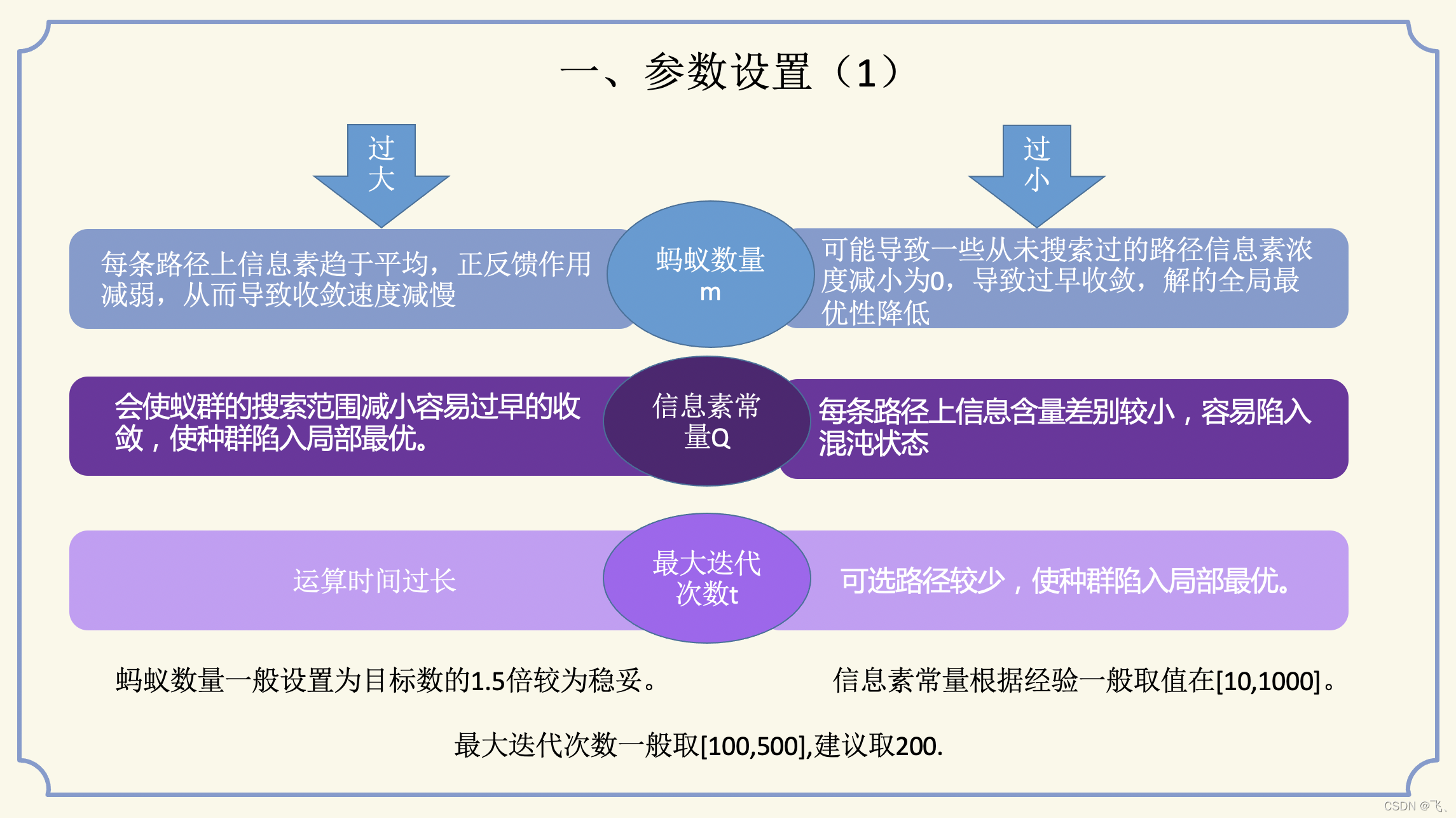
实例

function D = Distance(citys)
%% 计算两两城市之间的距离
% 输入:各城市的位置坐标(citys)
% 输出:两两城市之间的距离(D)
 
n = size(citys, 1);
D = zeros(n, n);
for i = 1: n
    for j = i + 1: n
            D(i, j) = sqrt(
			            	(citys(i, 1) - citys(j, 1))^2 + 
			            	(citys(i, 2) - citys(j, 2))^2
            			  );
            D(j, i) = D(i, j);
    end
    %对角线的值为0，但由于后面的启发因子要取倒数，因此用一个很小数代替0
    D(i, i) = 1e-4;              
end

%% I. 清空环境
clc
clear all
%% II. 符号说明
% C                         -- n个城市的坐标
% NC_max                    -- 最大迭代次数
% m                         -- 蚁群中蚂蚁的数量，一般设置为城市的1.5倍
% D(i, j)                   -- 两城市i和之间的距离
% Eta(i, j) = 1 ./ D(i, j)  -- 启发函数
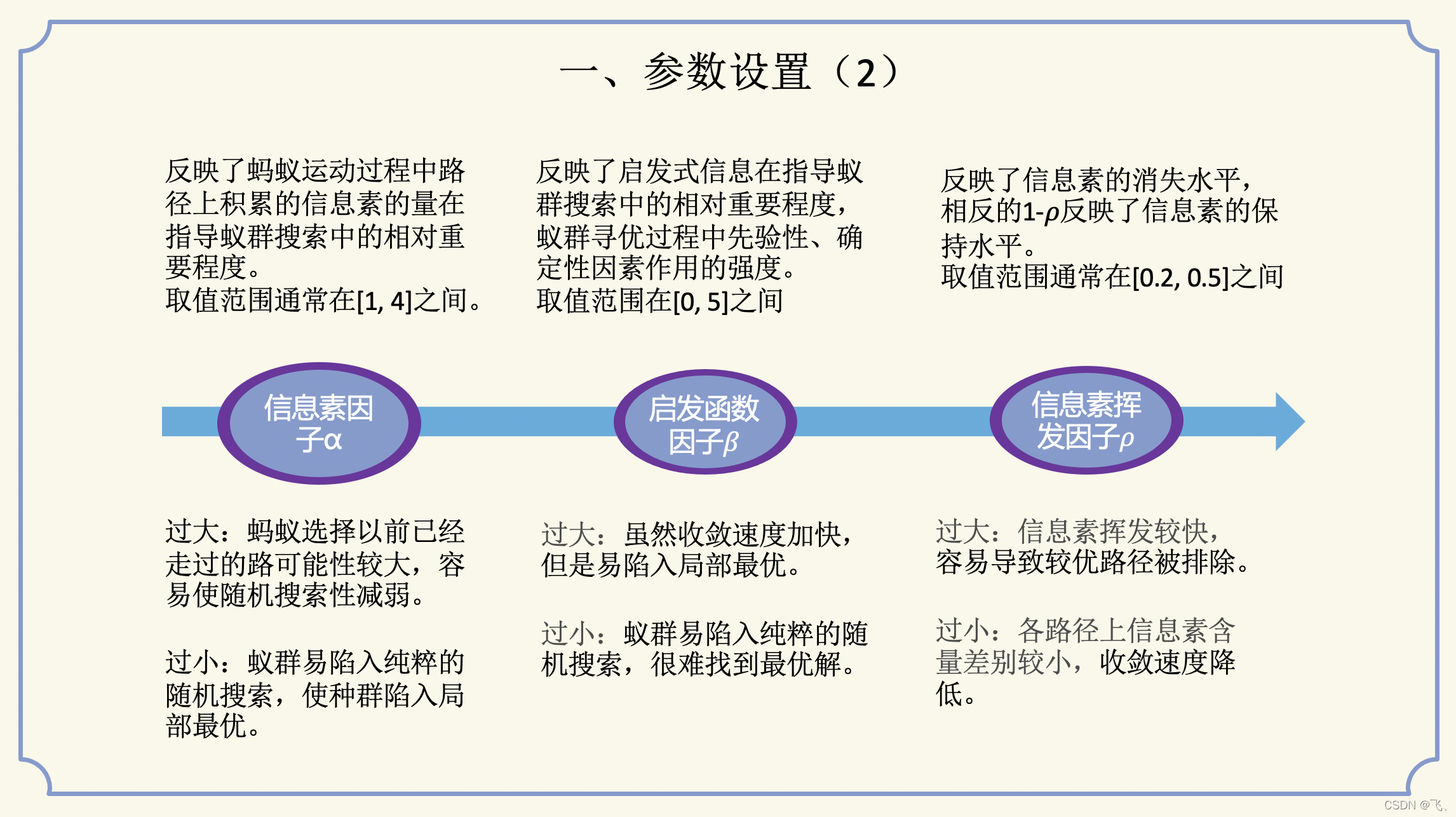
% alpha                     -- 表征信息素重要程度的参数
% beta                      -- 表征启发函数重要程度的参数
% rho                       -- 信息素挥发因子
% Q                         --
% rBest                     -- 各代最佳的路线
% lBest                     -- 各代最佳路线的长度
% lAverage                  --各代的平均长度
 
%% III. 导入城市位置数据
citys = [18.4700   95.1000
     16.4700   94.6400
     20.0900   94.5400
     14.3900   93.3700
     25.2300   97.2400
     22.0000   93.0500
     23.4700   92.0200
     16.2000   96.2900
     17.3000   97.3800
     13.0500   98.1200
     15.5300   97.3800
     24.5200   95.5900
     16.4100   97.1300
     15.0900   92.5500];
 
%% IV. 计算距离矩阵
D = Distance(citys);                                        % 计算距离矩阵
n = size(D, 1);                                             % 城市的个数
  
%% V. 初始化参数
NC_max = 200;                                               % 最大迭代次数，取100~500之间
m = 22;                                                     % 蚂蚁的个数，一般设为城市数量的1.5倍
alpha = 1;                                                  % α 选择[1, 4]比较合适
beta = 4;                                                   % β 选择[3 4 5]比较合适
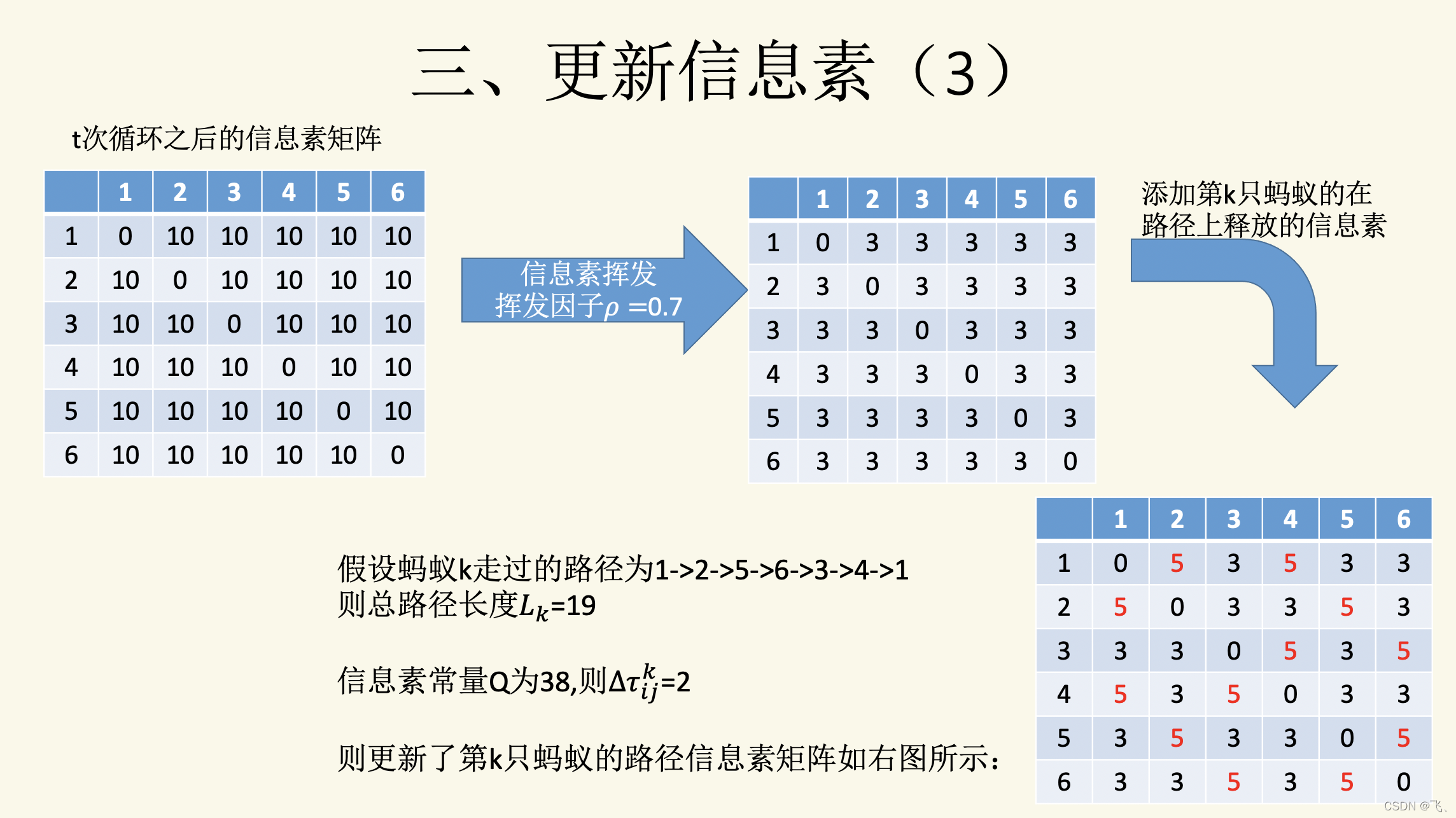
rho = 0.2;                                                  % ρ 选择[0.1, 0.2, 0.5]比较合适
Q = 20;
NC = 1;                                                     % 迭代次数，一开始为1
 
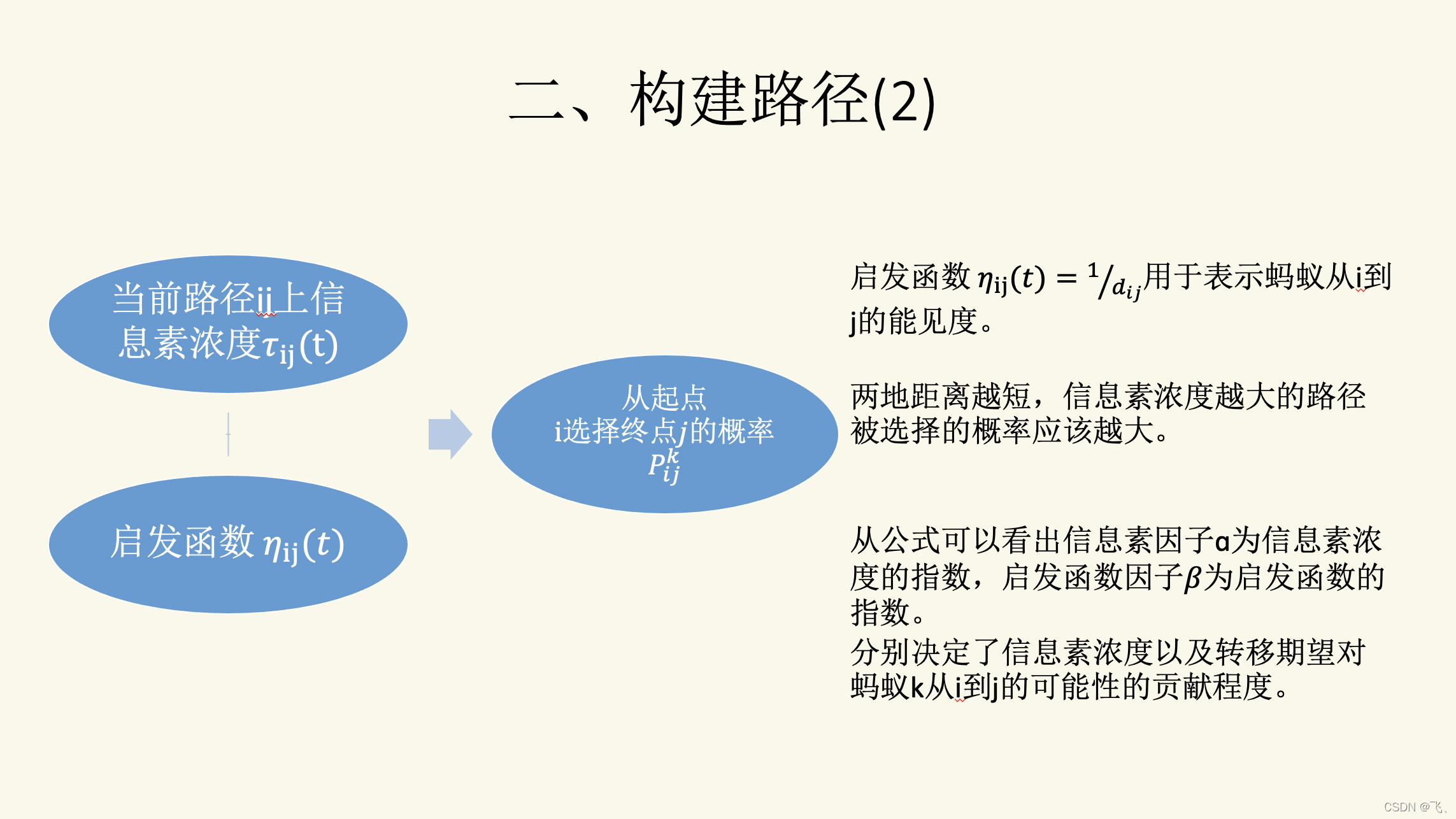
Eta = 1 ./ D;                                               % η = 1 / D(i, j) ,这里是矩阵
Tau = ones(n, n);                                           % Tau(i, j)表示边(i, j)的信息素量，一开始都为1
Table = zeros(m, n);                                        % 路径记录表
 
rBest = zeros(NC_max, n);                                   % 记录各代的最佳路线
lBest = inf .* ones(NC_max, 1);                             % 记录各代的最佳路线的总长度
lAverage = zeros(NC_max, 1);                                % 记录各代路线的平均长度
 
%% VI. 迭代寻找最佳路径
while NC <= NC_max
    % 第1步：随机产生各个蚂蚁的起点城市
    start = zeros(m, 1);
    for i = 1: m
        temp = randperm(n);
        start(i) = temp(1);
    end
    Table(:, 1) = start;                                    % Tabu表的第一列即是所有蚂蚁的起点城市
    citys_index = 1: n;                                     % 所有城市索引的一个集合
    % 第2步：逐个蚂蚁路径选择
    for i = 1: m
        % 逐个城市路径选择
        for j = 2: n
            tabu = Table(i, 1: (j - 1));                    % 蚂蚁i已经访问的城市集合（称禁忌表）
            allow_index = ~ismember(citys_index, tabu);
            Allow = citys_index(allow_index);               % Allow表：存放待访问的城市
            P = Allow;
             
            % 计算从城市j到剩下未访问的城市的转移概率
            for k = 1: size(Allow, 2)                       % 待访问的城市数量
                P(k) = Tau(tabu(end), Allow(k))^alpha * Eta(tabu(end), Allow(k))^beta;
            end
            P = P / sum(P);                                 % 归一化
             
            % 轮盘赌法选择下一个访问城市（为了增加随机性）
            Pc = cumsum(P);
            target_index = find(Pc >= rand);
            target = Allow(target_index(1));
            Table(i, j) = target;      
        end
    end
     
    % 第3步：计算各个蚂蚁的路径距离
    length = zeros(m, 1);
    for i = 1: m
        Route = Table(i, :);
        for j = 1: (n - 1)
            length(i) = length(i) + D(Route(j), Route(j + 1));
        end
        length(i) = length(i) + D(Route(n), Route(1));
    end
     
    % 第4步：计算最短路径距离及平均距离
    if NC == 1
        [min_Length, min_index] = min(length);
        lBest(NC) = min_Length;
        lAverage(NC) = mean(length);
        rBest(NC, :) = Table(min_index, :);
    else
        [min_Length, min_index] = min(length);
        lBest(NC) = min(lBest(NC - 1), min_Length);
        lAverage(NC) = mean(length);
        if lBest(NC) == min_Length
            rBest(NC, :) = Table(min_index, :);
        else
            rBest(NC, :) = rBest((NC - 1), :);
        end
    end
    % 第5步：更新信息素
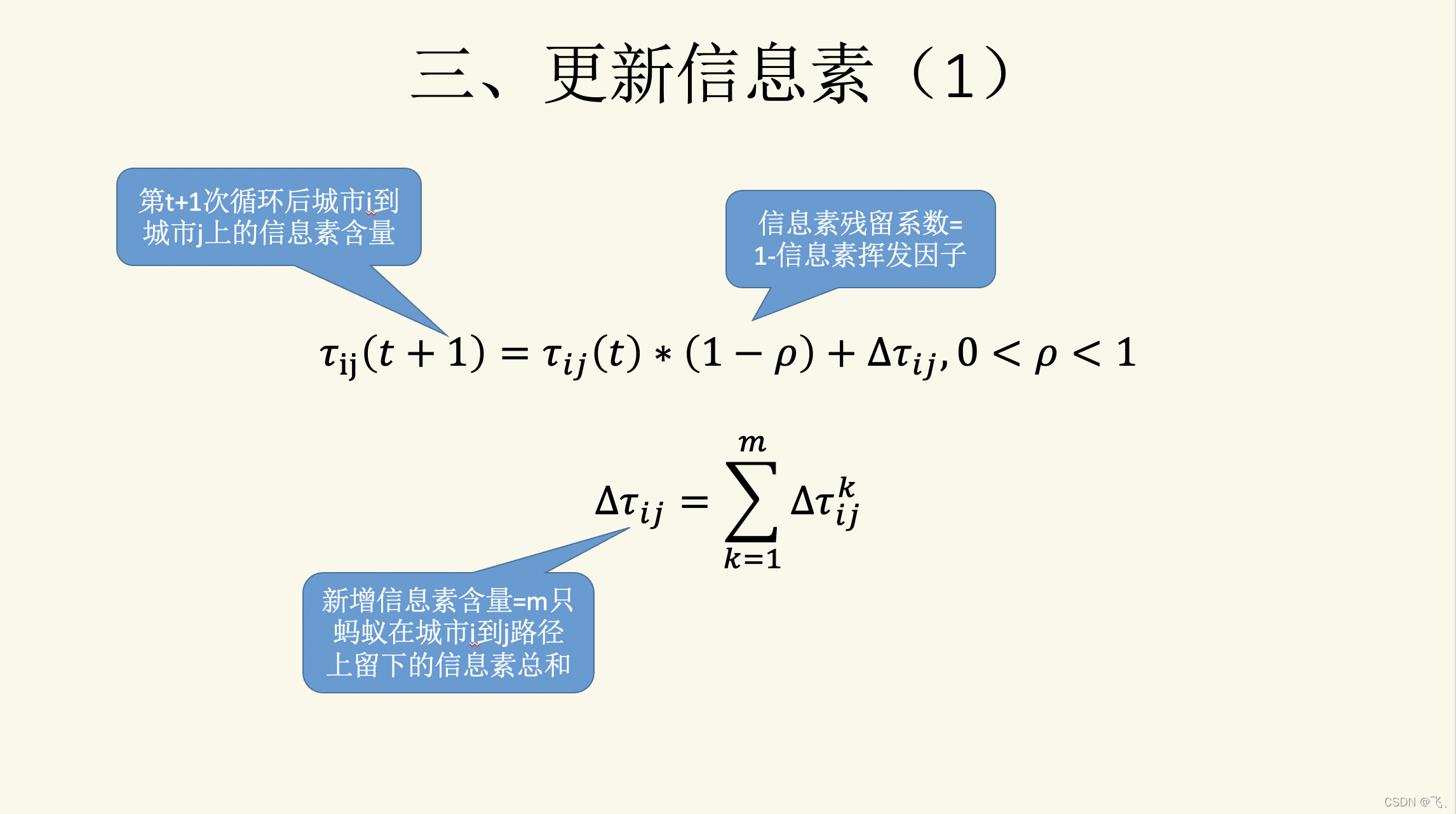
    Delta_tau = zeros(n, n);
    for i = 1: m         
        for j = 1: (n - 1)
            Delta_tau(Table(i, j), Table(i, j + 1)) = Delta_tau(Table(i, j), Table(i, j + 1)) + Q / length(i);
        end
        Delta_tau(Table(i, n), Table(i, 1)) = Delta_tau(Table(i, n), Table(i, 1)) + Q / length(i);
    end
    Tau = (1 - rho) .* Tau + Delta_tau;
 
    % 第6步：迭代次数加1，并且清空路径记录表
    NC = NC + 1;
    Table = zeros(m, n);
end
%% VII. 结果显示
[shortest_Length, shortest_index] = min(lBest);
shortest_Route = rBest(shortest_index, :);
disp(['最短距离:' num2str(shortest_Length)]);
disp(['最短路径:' num2str([shortest_Route shortest_Route(1)])]);
 
%% VIII. 绘图
figure(1)
plot([citys(shortest_Route,1); citys(shortest_Route(1),1)],...
     [citys(shortest_Route,2); citys(shortest_Route(1),2)],'o-');
grid on
for i = 1: size(citys, 1)
    text(citys(i, 1), citys(i, 2), ['   ' num2str(i)]);
end
text(citys(shortest_Route(1), 1), citys(shortest_Route(1), 2), '       起点');
text(citys(shortest_Route(end), 1), citys(shortest_Route(end), 2), '       终点');
xlabel('城市位置横坐标')
ylabel('城市位置纵坐标')
title(['蚁群算法优化路径(最短距离: ' num2str(shortest_Length) ')'])
figure(2)
plot(1: NC_max, lBest, 'b', 1: NC_max, lAverage, 'r:')
legend('最短距离', '平均距离')
xlabel('迭代次数')
ylabel('距离')
title('各代最短距离与平均距离对比')