通过一个单相逆变器仿真深度学习PR控制器

卡洛斯伊

已于 2024-07-22 09:41:43 修改

阅读量3.1k

点赞数 33

CC 4.0 BY-SA版权

分类专栏：电源控制Simulink代码生成文章标签：单片机嵌入式硬件

于 2024-07-04 15:22:44 首次发布

本文链接：https://blog.youkuaiyun.com/weixin_42665184/article/details/140171825

电源控制Simulink代码生成专栏收录该内容

15 篇文章

订阅专栏

前言

在项目开发中常用PI控制器，这次在做单相逆变器的时候发现PI控制器在有些工况有局限性，于是引入了PR控制器。简单来说当控制器的输入是直流量大多用PI控制器，当控制器输入是一定频率的正弦量时PR控制器相比于PI控制器就好很多。如在单相逆变的电压环输入的就是目标电压的参考，给定值是50Hz,220V的交流电。如果要用PI控制器需要对给定电压进行变换转换成直流量，但是由于50Hz的频率比较低，转换后的直流量控制起来响应和带宽做不高。

在电机控制里电流环也可以采用PR控制器，需要输入当前电频率。

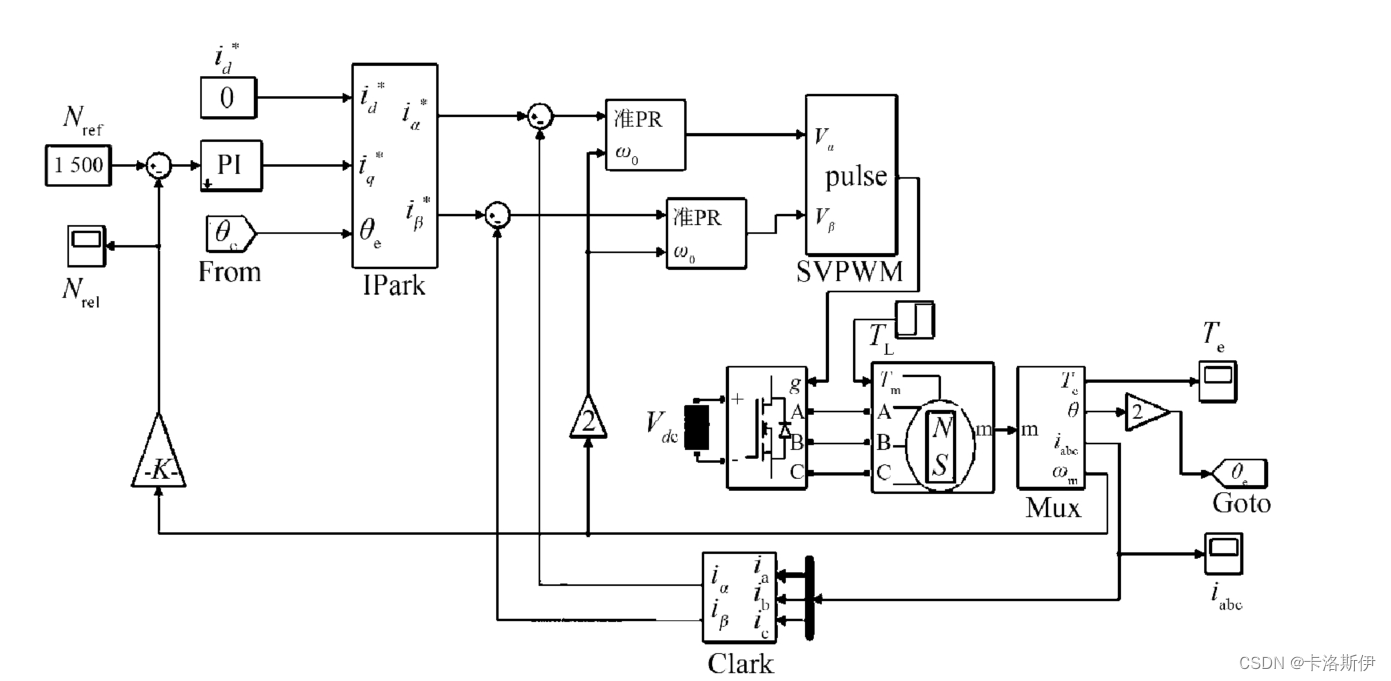
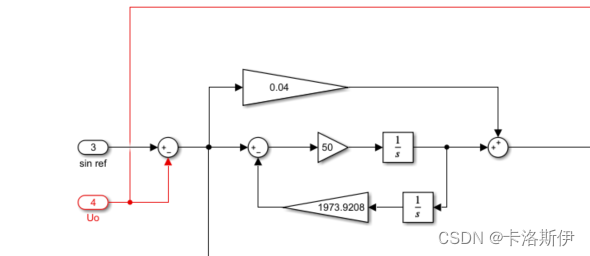
在单/三相FPC整流和逆变同样也可以有类似的用法。如下图是单相逆变电压环简化的PR控制器。

PR控制器的理论

很多论文都有下面这样的描述，这里不再过多解释，网上对PR控制器的解释很多，包括伯德图等。这里主要以改进型的PR控制器根据实际的工程需要如何建模仿真。

PR控制器不同表达式及其建模

在实际开发中，s域的传递函数是没法写成C代码或者直接生成代码的，需要对其进行离散化，或者写成积分形式，或者写成差分方程的形式，直接用离散传递函数也是可以生成代码的，具体用哪种形式可以从方便或者代码量方面去考虑。

如下是能在单相系统中正常工作的参数。

Tprs是离散后的采样频率，对应控制环路执行频率，暂定70Khz.

Kpr_p，Kpr_r类似于PI的控制参数。
wcpr控制器的截止频率
wopr谐振频率，对应给定的参考变量频率，如果是电压环就是给定的参考交流电压频率。为了方便建模可以考虑把Kp单独拿出来，也可以整合成一个完整的传递函数。

根据PR控制器的传递函数

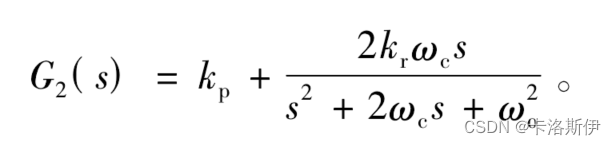
PR控制器连续积分组合及模型

写成积分组合形式Kp单独拿出来：

$R(s)=\frac{y(s)}{u(s)}=\frac{2K_{r}W_{c}s}{s^{2}+2W_{c}s+W_{o}^{2}}$

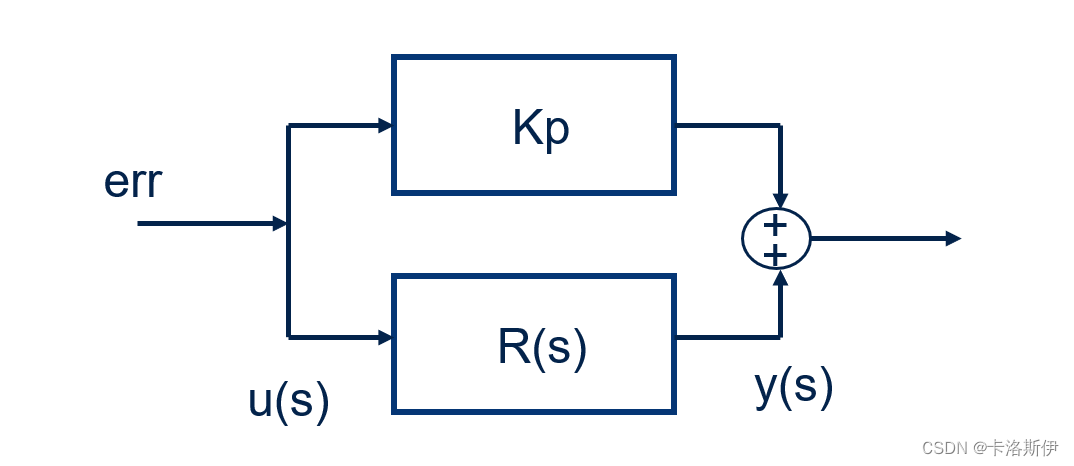
分子分母调换一下：

$\frac{u(s)}{y(s)}=\frac{s^{2}+2W_{c}s+W_{o}^{2}}{2K_{r}W_{c}s}=\frac{s}{2K_{r}W_{c}}+\frac{1}{K_{r}}+\frac{W_{o}^{2}}{2K_{r}W_{c}s}$

把u(s)提出来：

$u(s)=\frac{s}{2K_{r}W_{c}}*y(s)+\frac{1}{K_{r}}*y(s)+\frac{W_{o}^{2}}{2K_{r}W_{c}s}*y(s)$

再把y(s)挪到等号左边：

$\frac{s}{2K_{r}W_{c}}*y(s)=u(s)-\frac{1}{K_{r}}*y(s)-\frac{W_{o}^{2}}{2K_{r}W_{c}s}*y(s)$

得到如下的表达式：

$y(s)=\left [ u(s)-\frac{1}{K_{r}}*y(s)-\frac{W_{o}^{2}}{2K_{r}W_{c}s}*y(s) \right ]*\frac{2K_{r}W_{c}}{s}$

到这一步就可以用Simulink搭成积分的形式了。

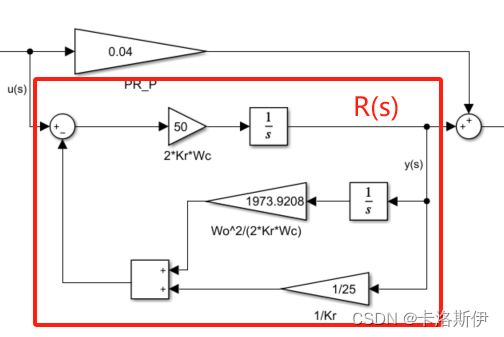
实际中，把1/Kr这一项去掉也不影响系统正常工作，所以有些PR控制器可能没有这一项。如下所示：

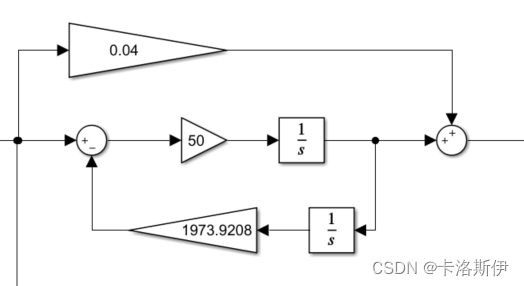
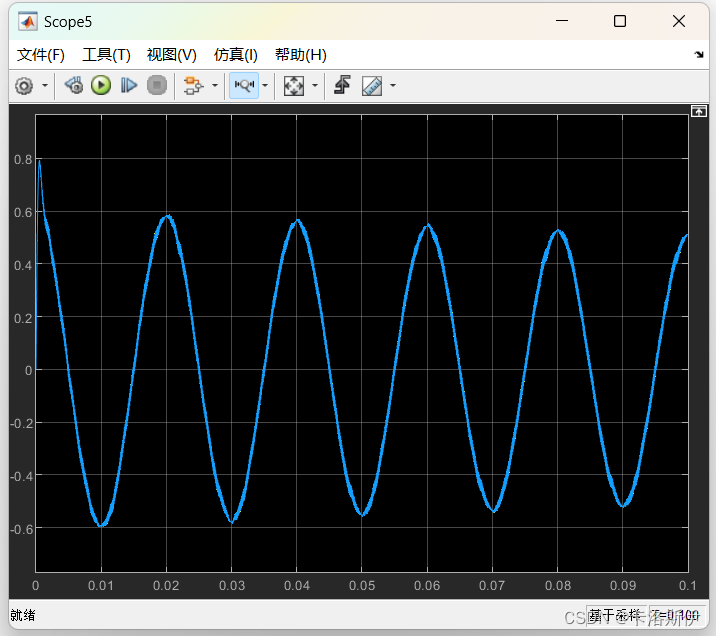
对比如下，有1/Kr和没有区别不是很大，特别是Kr选取比较大的时候，这一项的影响较小，实际中可以根据取值决定是否需要，可以节省那么一丢丢的算力。

黄色省掉了1/Kr的项，蓝色保留

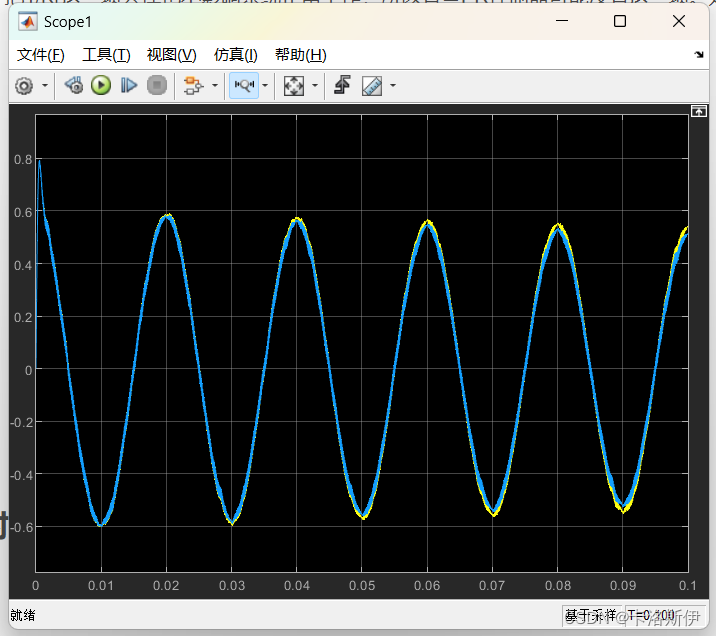
PR控制器连续传递函数及模型

采用连续传递函数直接控制，如下是包含Kp的控制器完整传递函数，在仿真中直接用Transfer Fcn模块做控制器也是可以的。

和通过模块搭建的积分形式在相同输入的情况下，输出完全重合，这也从侧面验证了前面搭的积分组合形式没任何问题。

PR控制器离散积分及模型

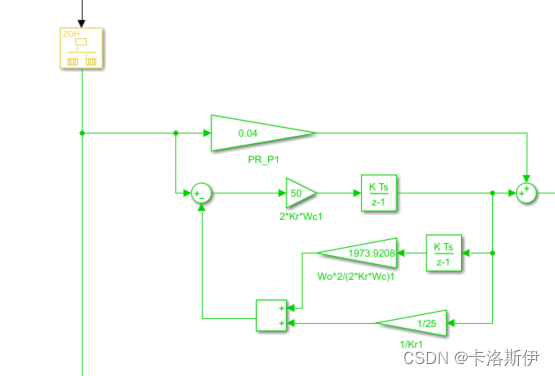
前面都是连续系统的仿真，实际工程需要离散化，对于积分组合形式只需要加上个速率转换，把连续积分换成离散积分就能得到离散积分的形式，如下：

Matlab可以通过c2d的函数把连续传递函数转换成离散传递函数，如下：

只需要根据实际工程中的控制器执行频率设置采样时间和离散方式就可以了，这里选择tustin双线性变换的离散方法。

Dpr_Z=c2d(Cpr_s,Tprs,'tustin');

离散化的方法有很多：前向差分法、后向差分法、双线性变换、预插值双线性变换、脉冲响应不变法、零极点匹配法、零阶保持不变法、一阶保持不变法，实际的嵌入式系统用零阶保持和双线性变换都差不多，反正都是通过Matlab直接得到离散化后的传递函数，Bode图也都差不多。

PR控制器离散传递函数及模型

R(s)离散化后得到R(z)

这里有个坑需要注意，按照得到的离散传递函数直接构建的控制器输出和连续传递函数控制器输出不一样，完全不能让系统收敛，如下图：

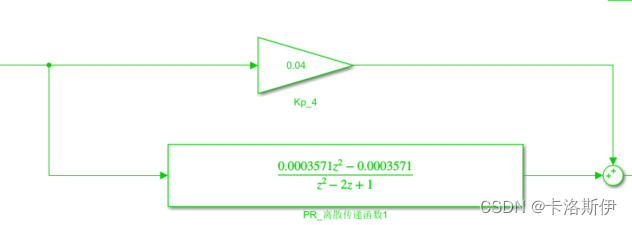
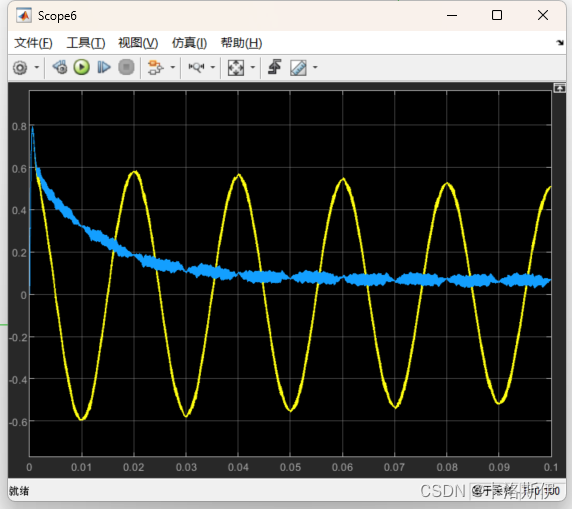
这里需要把Matlab的数据显示精度改成long。不然会影响控制器的正常工作，改完后得到的传递函数如下：

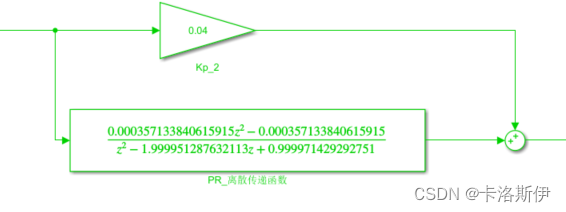
连续的PR控制器和离散的PR控制器输出重合。

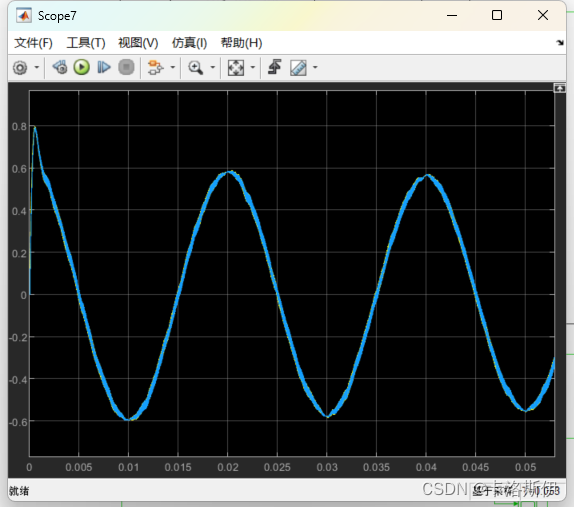
细节上连续的更光滑，离散的会有70Khz的突变，不影响实际的控制系统。

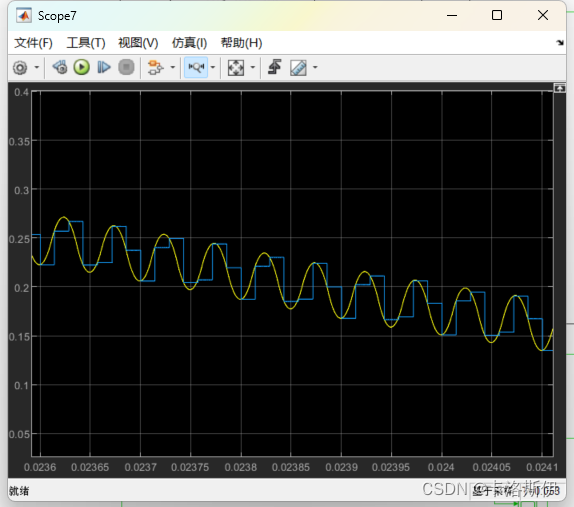
PR控制器差分方程及模型

这里只对R(z)进行差分方程化，其实在前面离散积分组合，离散传递函数都可以直接生成代码应用到工程里面，这里再多一个差分方程的形式方便另一种方式手写代码实现。

为了方便差分方程的推导，可以把离散传递函数写成表达式：

$R(z)=\frac{az^{2}-a}{z^{2}-bz+c}=\frac{y(z)}{x(z)}$

分子分母同时除以z^2:

$\frac{a-az^{-2}}{1-bz^{-1}+cz^{-2}}=\frac{y(z)}{x(z)}$

交叉相乘提出y(z):

$y(z)=bz^{-1}y(z)-cz^{-2}y(z)+ax(z)-az^{-2}x(z)$

把上式写成差分方程：

$y(k)=by(k-1)-cy(k-2)+ax(k)-ax(k-2)$

根据差分方程建模得到：

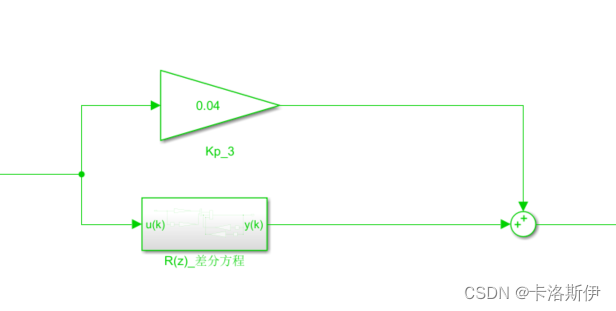
不管用哪种形式作为控制器，同样的输入经过控制器后输出都一样，证明不管是传递函数还是差分方程还是积分组合的方式模型搭建都没有错误。

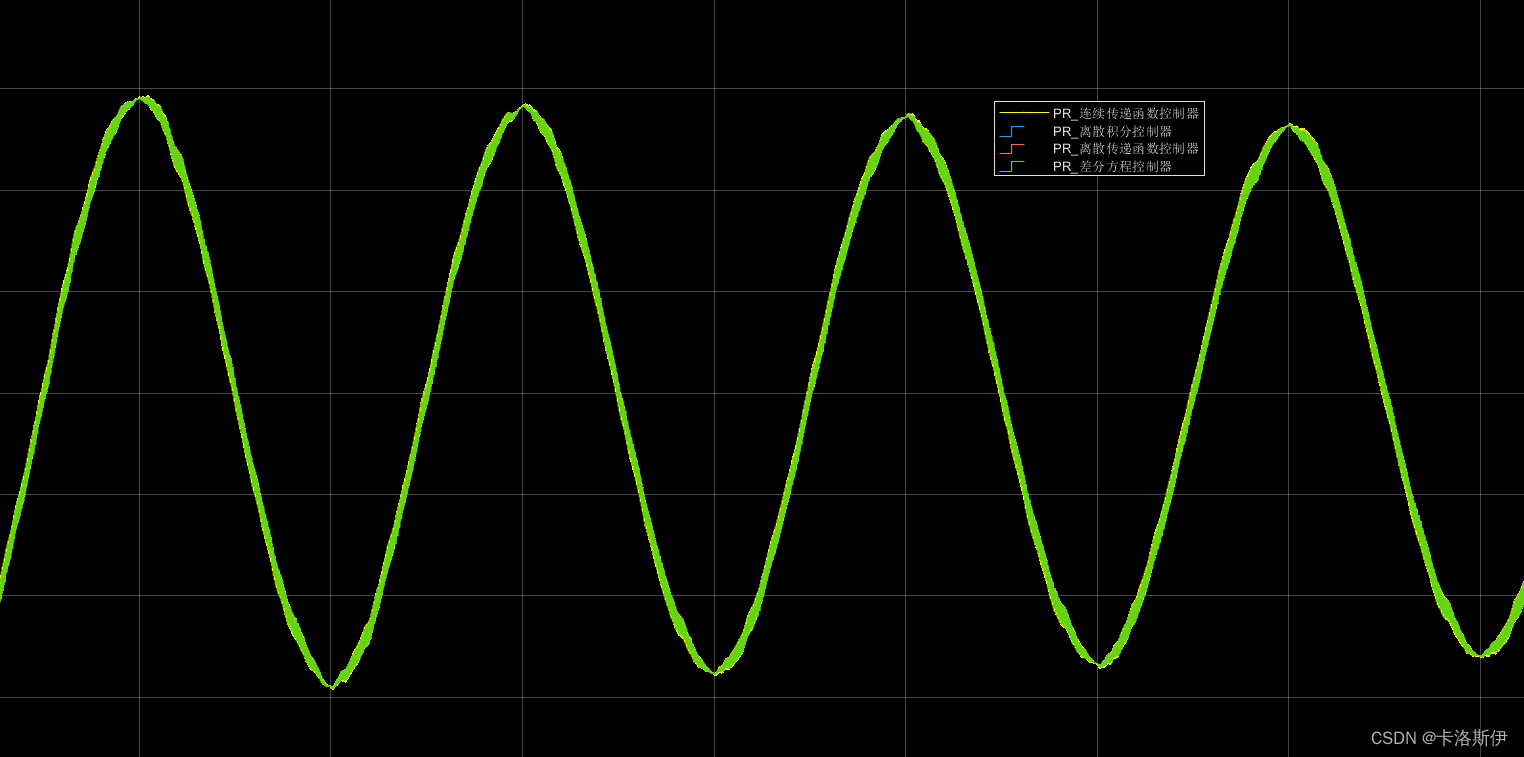
系统仿真效果

最后通过一个单相逆变器系统仿真验证

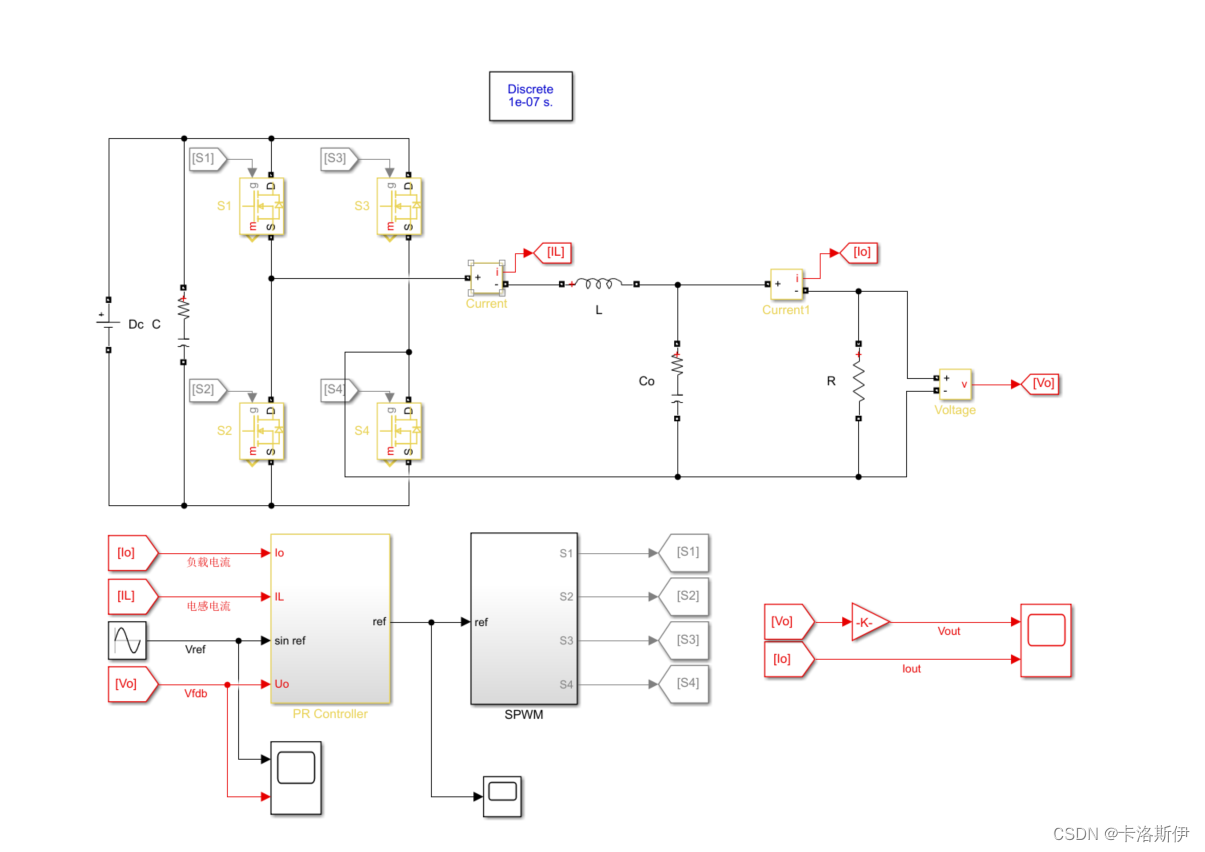
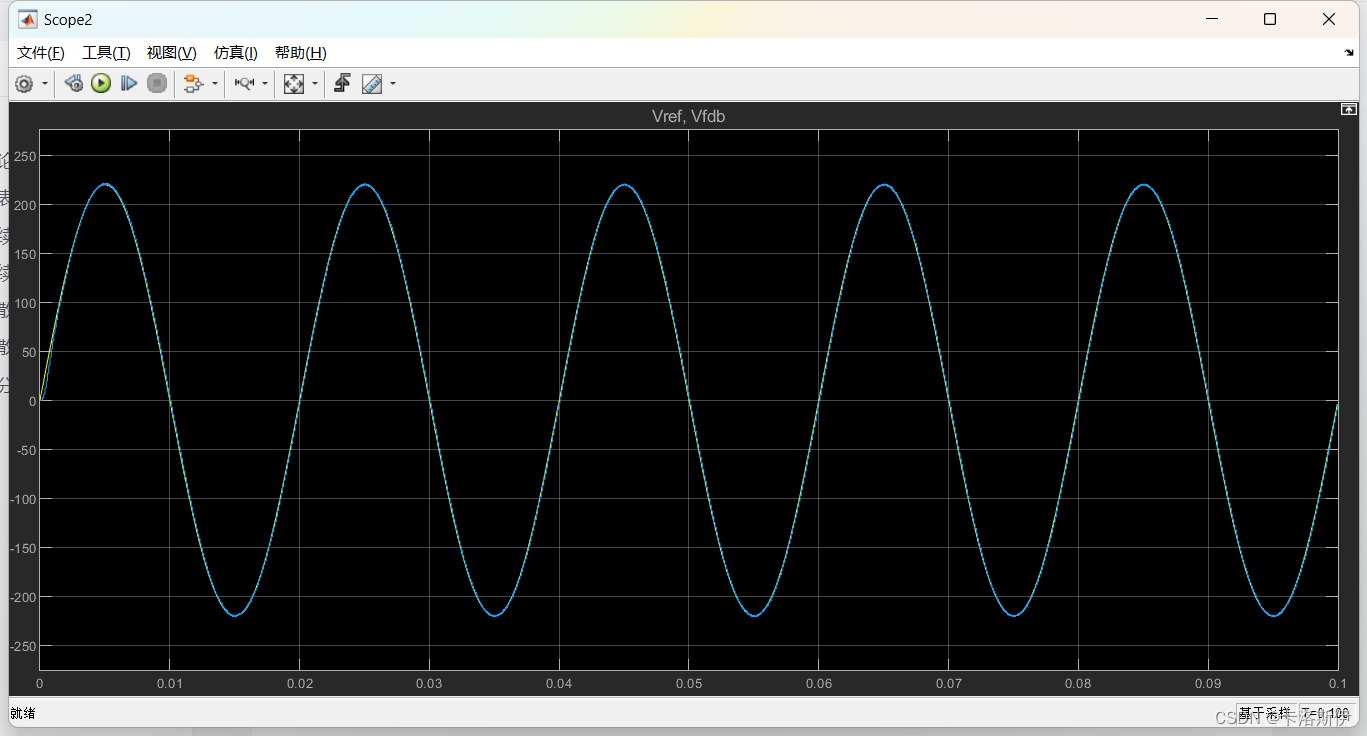
给定电压和反馈电压重合

输出的交流电压和电流

总结

通过一个单相逆变器，引入了PR控制器，从仿真的角度来讲不管是s域传递函数还是Z域传递函数仿真都没有问题，实际工程中程序是在单片机里执行，需要把PR控制器离散化，对于手写代码和基于模型的自动代码生成来讲可以考虑差分方程或者积分组合的形式，不考虑去饱和直接写离散传递函数也可以。

模型下载地址:https://download.youkuaiyun.com/download/weixin_42665184/89557195?spm=1001.2014.3001.5503