算法图解之广度优先搜索

广度优先搜索

主要内容

• 图初步了解；
• 广度优先搜索，用图解释最短路径等问题；
• 有向图和无向图；
• 拓扑排序，节点之间的依赖关系。

图

简介

引例

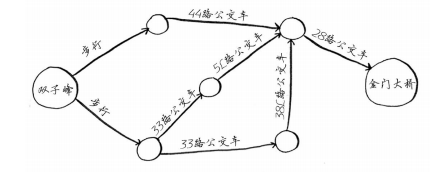
如何从双子峰去金门大桥？摆在你面前有若干条路径。如何找出最短的路径的算法称为广度优先搜索。

那么，什么是图？图表示圈（节点）代表的主体之间的关系，由节点和边组成。

广度优先搜索

在探索最短路径之前，你可能需要了解的问题是：有路径吗？
从起点出发，从起点之后的每一个节点为中心，遍历所有以该中心的所有关联节点，看是否有目的点，这就是广度优先搜索。
接下来就是查找最短路径了。另外，鉴于有一个优先的问题，就是某些节点具有更高的优先级，引入先入先出的数据结构——队列。、
实现：

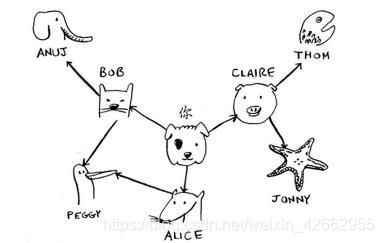
python代码：

graph["you"] = ["alice", "bob", "claire"] 
graph["bob"] = ["anuj", "peggy"] 
graph["alice"] = ["peggy"] 
graph["claire"] = ["thom", "jonny"] 
graph["anuj"] = [] 
graph["peggy"] = [] 
graph["thom"] = [] 
graph["jonny"] = [] 

有向图和无向图

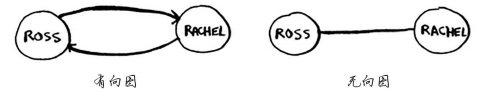
Anuj、Peggy、Thom和Jonny都没有邻居，这是因为虽然有指向他们的箭头，但没有从他们出发指向其他人的箭头。这被称为有向图（directed graph），其中的关系是单向的。因此，Anuj是Bob的邻居，但Bob不是Anuj的邻居。无向图（undirected graph）没有箭头，直接相连的节点互为邻居。例如，下面两个图是等价的。

实现：

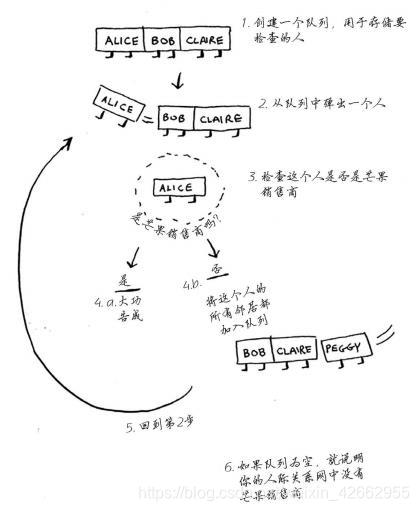
代码：

def search(name): 
 search_queue = deque() 
 search_queue += graph[name] 
 searched = [] 
 while search_queue: 
person = search_queue.popleft() 
if not person in searched:
if person_is_seller(person): 
print person + " is a mango seller!" 
return True 
else: 
search_queue += graph[person] 
searched.append(person)
 return False 
 
search("you") 

运行时间

广度优先搜索的运行时间为O（人数+边数），通常写作O（V+E）[定点数和边数]。

总结

• 广度优先搜索指出是否有从A到B的路径；
• 有->广度优先搜索将找出最短路径;
• 寻找最短路径问题，可尝试使用图来建立模型，使用广度优先搜索来解决问题;
• 有向图中的边为箭头，箭头的方向指定了关系的方向;
• 无向图中的边不带箭头，其中的关系是双向的;
• 你需要按加入顺序检查搜索列表中的人，否则找到的就不是最短路径，因此搜索
  列表必须是队列。