整数划分问题之递归法

参考博客

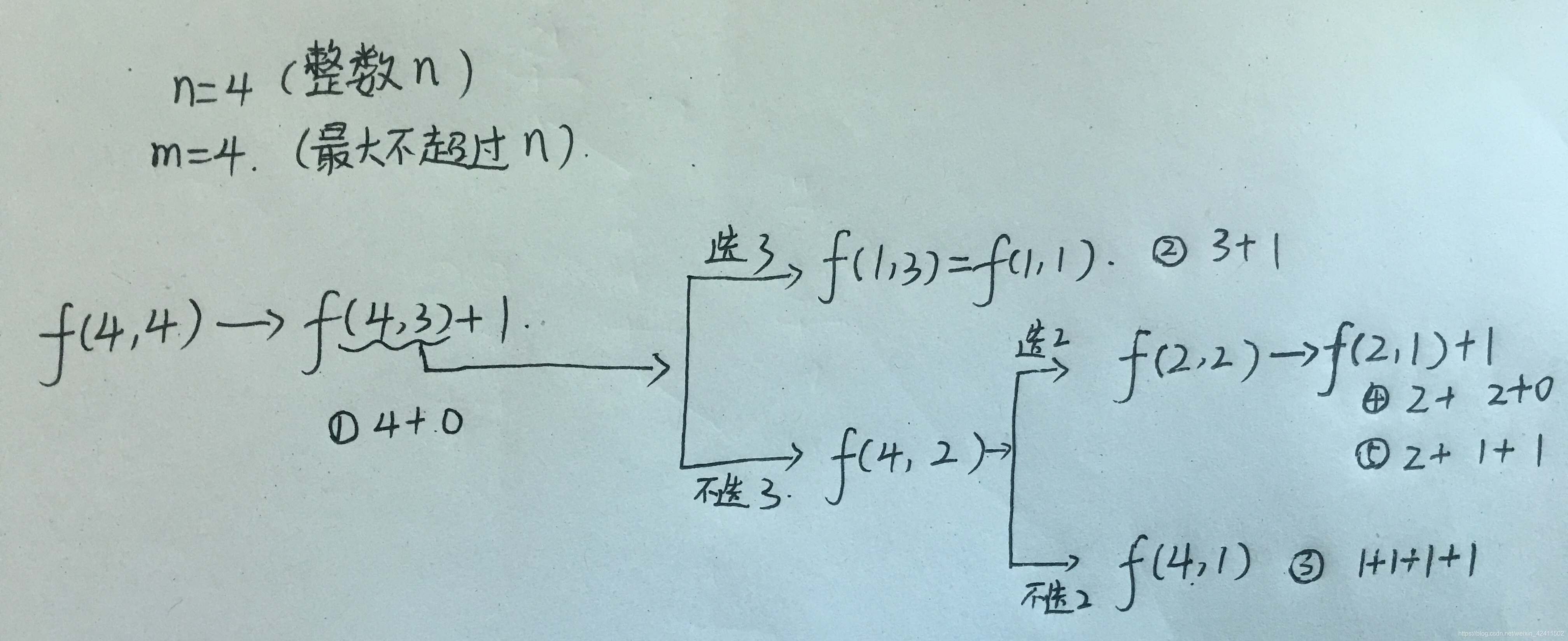
整数最大划分类似这样子
4 = 4;

4 = 3 + 1;

4 = 2 + 2;

4 = 2 + 1 + 1;

4 = 1 + 1 + 1 + 1;
那么4的最大划分有5个

解决对整数n的最大划分
需要一个最大不超过n的整数 m。

分成4种情况

1. 当n=1或者m=1的时候，n个1相加，一种情况了
2. 当n=m&&(m>1)&&(n>1)的时候，需要分解拿出0+m这一项，然后f(n,n-1)
3. 当n<m的时候，理论上不存在所以需要改为f(n,n)
4. 当n>m的时候，有俩选择
   1.选择了m，那么f(n-m,m)
   2.没有选m,那么f(n,m-1)

递归耗时，母函数和dp也可以，日后补上

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<string.h>
#include<cstdlib>
#include<cstring>
#include<math.h>
#include<cmath>
#include<vector>
#include<map>
using namespace std;
int f(int n,int m)
{
    if(n==1||m==1)
    return 1;
    else if(n==m&&n>1)
    {
        return f(n,n-1)+1;
    }
    else if(n<m)
    {
        return f(n,n);
    }
    else if(n>m)
    {
        return f(n-m,m)+f(n,m-1);
    }
}
int main()
{
  int n;
  while(scanf("%d",&n)!=EOF)
  {
      printf("%d\n",f(n,n));
  }
   return 0;
}