向量组

---

• 向量组的向量添加分量(增维)和向量组增加向量

增加维度：高维相关低维相关，低维无关高维无关

增加向量：原来无关，增加后，若能α能由其余向量线性表示且表示法唯一，则增加后线性相关；若不能则无关(总之不一定)。原来相关，增加一个向量后，向量组还是线性相关，只不过它不一定能被其余向量线性表示。原来无关减少一个向量后，还是无关。原来相关减少一个向量后，若减少的是那个唯一能被其余向量线性表示的向量，则减少后无关；否则线性相关。

---

• 向量组的线性表出与线性相关

---

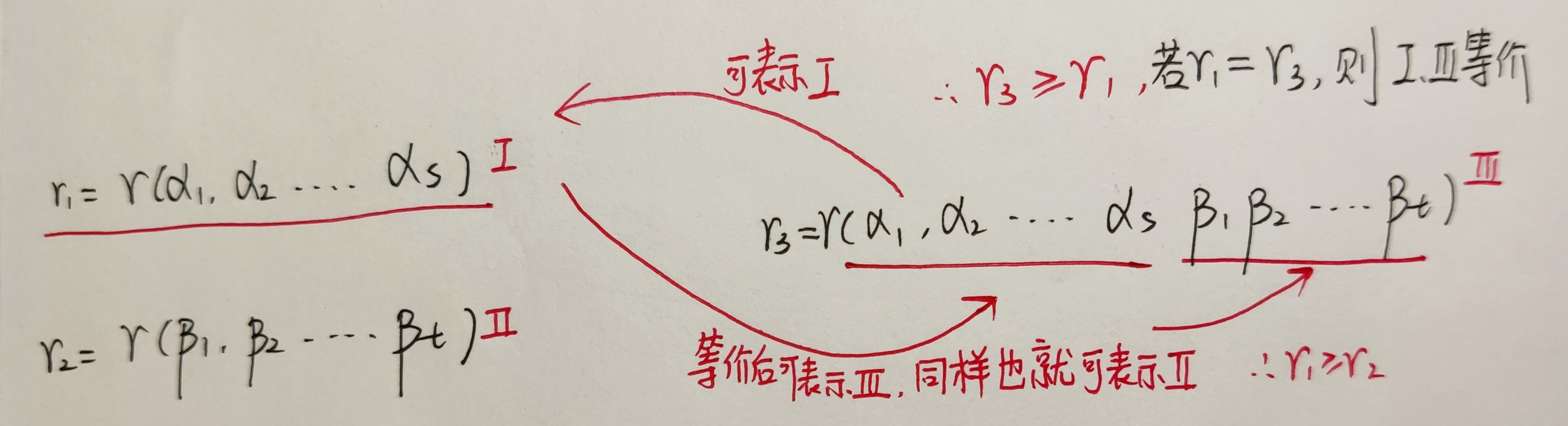
• 行阶梯(求极大无关组成员个数)

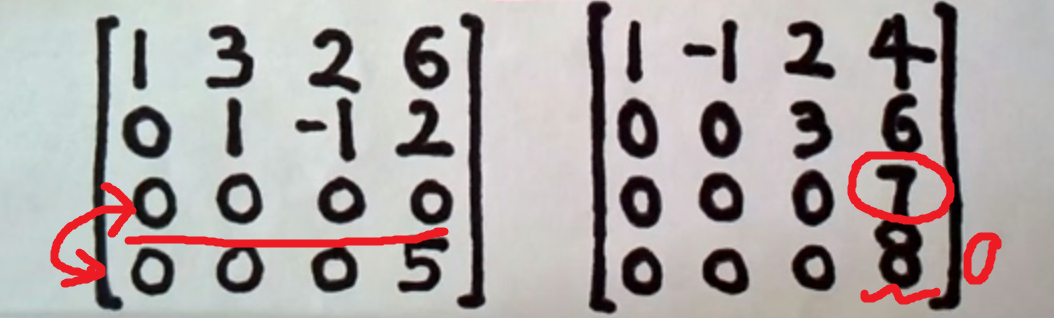
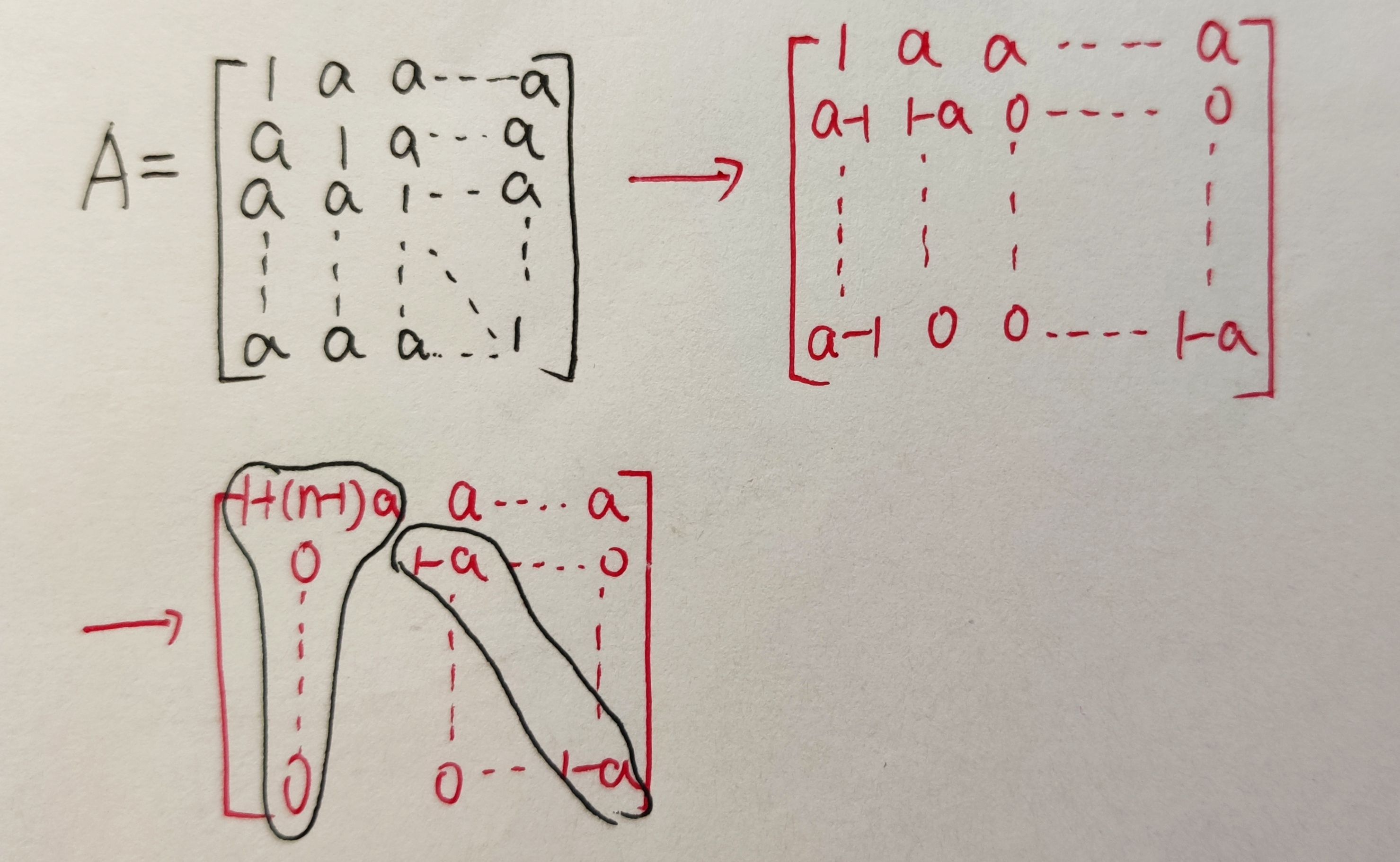
• 行最简(极大无关组表示其余向量)

---

• 求向量组的秩，所有极大线性无关组，并将其余的向量用极大线性无关组线性表出

1.矩阵初等行变换化成行阶梯矩阵
2.把所有阶梯上的，所在列向量取 秩的个数个
3.然后重新组成一个矩阵，重新画一画阶梯，看看阶梯数是否依旧等于秩的个数，是的话，这些个向量组就是一个极大无关线性组，否则就不是啦

所以直接取行阶梯矩阵每行第一个非0所在列所组成的新矩阵，阶梯数一定等于新矩阵的秩的个数，就一定是原矩阵的一个极大线性无关组。

• 注意点：

1.only求秩的时候，可行列混合变换，求解；其他情况都只能用单一行变换或者列变换求到底。
2.行阶梯到行最简的时候，不要使用列变换！！！
3.🔺有些新矩阵可以重新再行变换一下，就又是秩等于原矩阵的秩了，所以也是的，不要遗漏。

---

• 秩的不等式

---

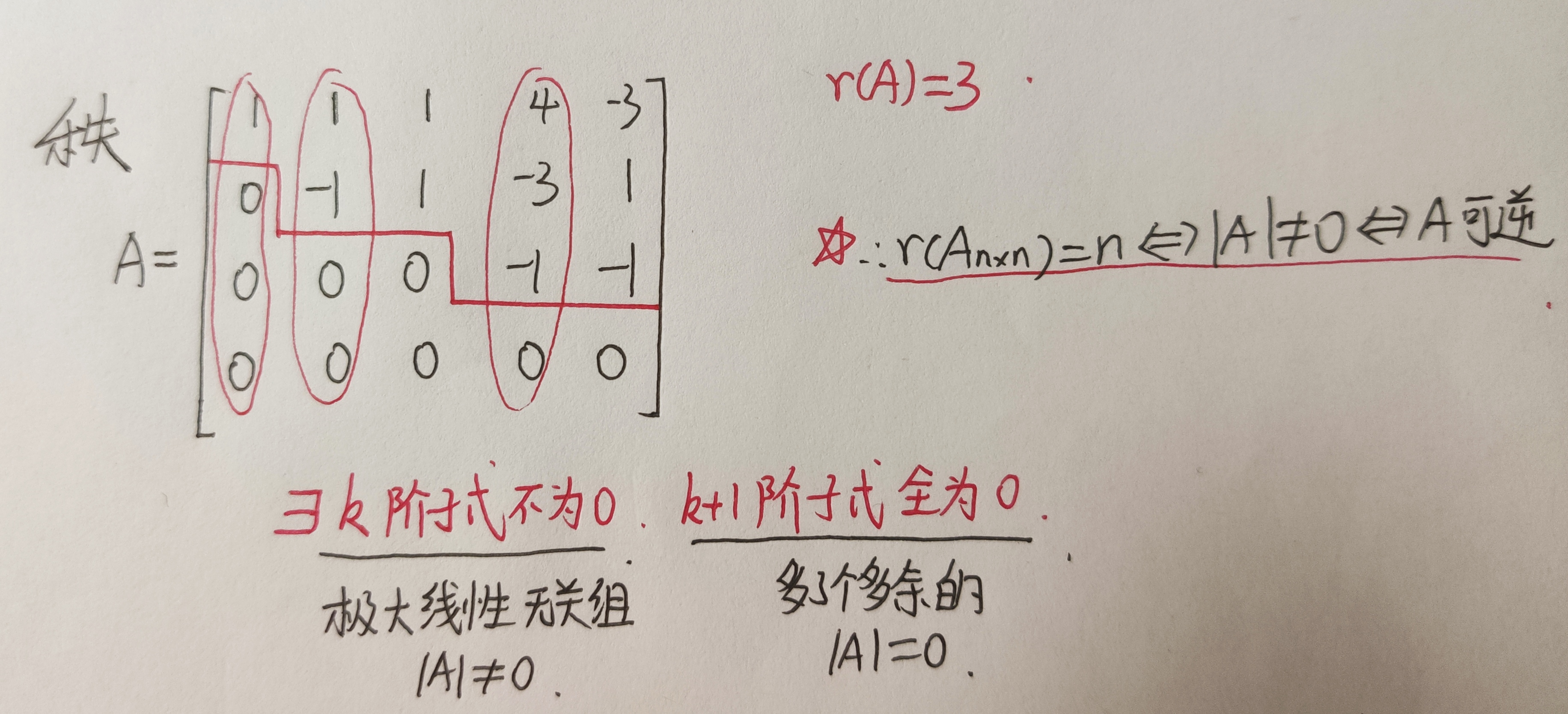
• 判断/证明正确命题(难点)

定理一：向量组 α1,α2,α3,α4.....αn(n>=2)线性相关的充要条件：向量组中至少有一个向量可由其余的n-1个向量线性表出。

方法1：举反例
方法2：反证法/逆否命题
方法3：定义法(同乘/带入重组)
方法4：秩
方法5：Ax=0,x解的情况

---

• 判断向量组是否线性相关/线性无关

n>m时

方法1：n个m维向量，线性无关

n=m时

方法1：以少表多，多的相关
方法2：凑系数
方法3：Ax=0，x是否只能是0解
方法4：|A|=0？线性相关(低阶)
方法5：化行阶梯，满秩？(高阶/非方阵)

n<m时

方法1：化行阶梯，打假，讨论秩
方法2：定理六，七(部分...，高维...)
方法3：以少表多，多的相关

---

• 抽象向量组判断线性表出，等价矩阵，等价向量组

问题1：初等行变换不改变行向量的线性相关性，初等列变换不改变列的线性相关性？对

A的行秩=A的列秩=矩阵的秩
初等行变换不改变行向量组的秩，初等列变换不改变列向量组的秩→初等行，列变换不改变矩阵的秩→初等变换不改变矩阵行列向量组的线性相关性

问题2:单个矩阵初等变换后,其行列向量组一定等价吗？一定。

问题3：矩阵A通过初等列(行)变换变成矩阵B，那么A,B的列(行)向量组等价吗？一定。

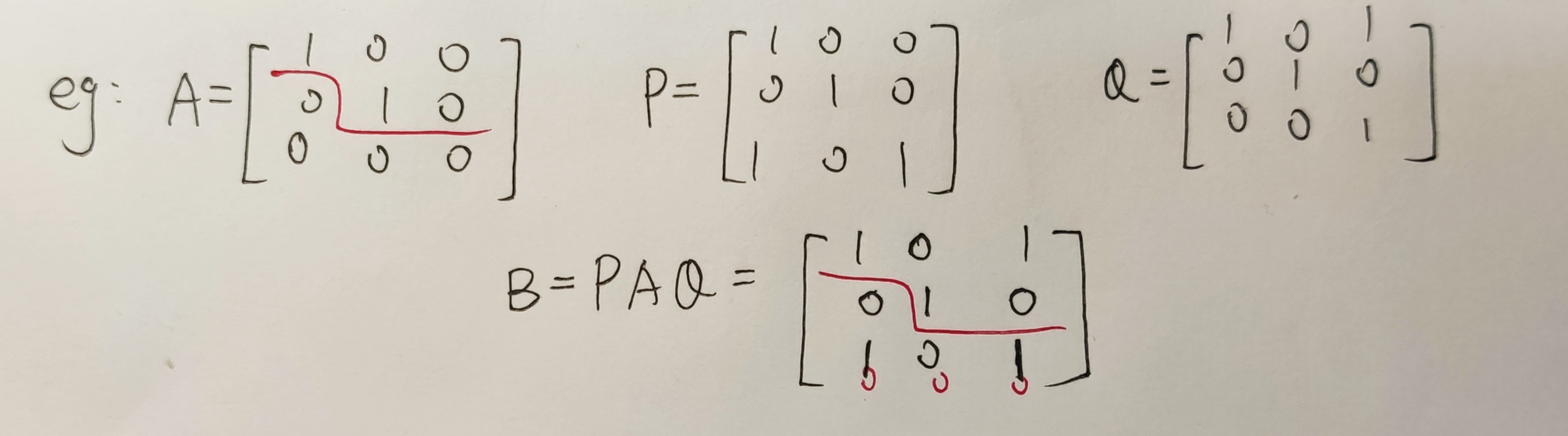
问题4：矩阵A通过初等行列混合变换变成矩阵B，那么A,B的行(列)向量组一定等价吗？不一定。

如图：B的1，3行(列)不能用A，的行(列)向量线性表示，故不等价

---

• 正交规范化，正交矩阵

---

• 向量空间

✋→ 补充理解篇—向量空间

日常简单三问：
1.某某到某某的过渡矩阵
2.A基下的坐标和B基下的坐标
3.求一个向量，使它在两组基下有相同坐标

---