前情提要:省选模拟赛 T1 势如猛虎,拼尽全力无法战胜。虽然这场 T2 才是签到题。
赛后才发现这个东西是整体二分。然后就想到了 CDQ 分治,准备一起学了。
cdq 就是发明者陈丹绮的名字缩写。感觉这人很牛。啥时候才能有 wsx 分治啊?
很显然 cdq 分治就是分治的一种方法,准确来说是一种思想。
进入主题。
cdq 分治
cdq 分治采用的是离线的方法,所以强制在线的题目 cdq 分治就寄了。
直接讲 cdq 的思想吧,因为我也编不出来 cdq 是怎么想到这个东西的了。
cdq 的分治有很多个思路的环,环环相扣。不妨一个一个来讲。
首先先把所有的询问都获取了,因为过会要离线。
然后就是第一个 cdq 分治的思路的环:
-
对于区间类(就是左端点和右端点)和点对类(类似坐标) 类问题的集合 { f ( l 1 , r 1 ) , f ( l 2 , r 2 ) , ⋯ , f ( l m , r m ) } \{f(l_1,r_1),f(l_2,r_2),\cdots,f(l_m,r_m)\} {f(l1,r1),f(l2,r2),⋯,f(lm,rm)}
-
这个时候,对于完全包含在区间 [ L , R ] [L,R] [L,R] 的问题集,先搞出一个中点 m i d mid mid,然后可以分为三类处理:
-
属于 [ L , m i d ) [L,mid) [L,mid) 的问题集。
-
属于 [ m i d , R ] [mid,R] [mid,R] 的问题集。
-
横跨 m i d mid mid 这个点的问题集。
-
很容易发现,前两种问题集都是类似递归的结构,所以,最终的重点就落在了如何求横跨中点的区间。
一旦能够求出这个东西,整个算法就结束了。
感觉有一点分治的味道了。
那么,这个时候 cdq 分治的妙处就体现在如何求横跨一个点的区间。 咋求呢?
我们想到了一个东西,尽管这很反直觉:归并排序求逆序对。
(虽然逆序对这个东西是用来求点对的,但是这也可以看作是区间)
归并排序就是用来求一个区间里面的逆序点对的。
观察归并排序,不难发现是将一个区间分成了两个区间,依次计算两个区间的答案并对两个子区间排序。然后答案合并。
而cdq 的心理就是:能不能将这种归并排序的方法拓展一下,来处理更加恶心的问题呢?
再次观察,就容易发现是先对两个左右区间按照某个偏序关系排序(例如在归并排序的时候这个偏序关系就是从小到大或是从大到小),然后就是两个游标在上面走来走去,并顺便计算答案。
于是这就是 cdq 分治的思想,说实话这东西思想和归并排序差不多,所以我也说不了多少。需要具体问题具体分析。
cdq 分治求解点对问题 / P3810 【模板】三维偏序(陌上花开)
题意已经足够简洁。
首先我们很容易想到先将 a i a_i ai 排一下序。然后就可以使用权值线段树和平衡树来维护二维偏序。
但是这样常数太大了,如果码风非常好的话也只能得到 70pts TLE。所以考虑使用 cdq 分治。
还是同样的思路,先对 a a a 的值排序。然后就知道了 a a a 的值一定是满足偏序的,只需要处理二维偏序即可。所以现在每一个就只有 ( b , c ) (b,c) (b,c) 两个值了。
首先我们需要知道怎么对左右子区间来排序。考虑在左右两个区间里面再次按照 b b b 来排序,但是这个东西并不能规约成一维偏序。
然后我们就需要思考怎么搞双游标了。
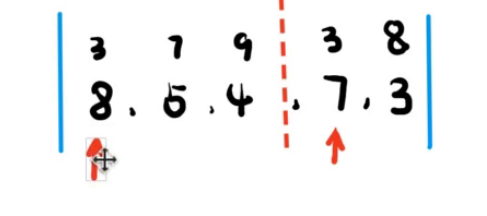
考虑归并排序是怎么搞双游标的。归并排序就是移动左边的游标,直到这个左边的游标和右边的游标对应的值不满足了某种偏序关系了就不移了。
我们考虑如法炮制。每一次将右边的游标向右移动一点,然后在左边的游标的 b b b 值小于等于右边游标的 b b b 值得情况下,计算有多少 b b b 值小于等于左边的游标的 b b b 值的坐标,其对应的 c c c 值也是小于等于右边游标的 c c c 值。
这显然可以使用树状数组维护。
因为归并排序的时间复杂度是 O ( n log n ) O(n \log n) O(nlogn),然后又树状数组就是 O ( log n ) O(\log n) O(logn)。合起来就是 O ( n log 2 n ) O(n \log^2 n) O(nlog2n)。
cdq 代码大体框架
使用左闭右开的区间可以很容易的取到中点。
#define mid ((l + r) >> 1)
struct node {
//something
} val[N], ori[N];//一个是排序后的顺序,一个是原始顺序
bool cmp1(node x, node y) {//在cdq外面的排序
//something
}
bool cmp2(node x, node y) {//cdq里面对左右子区间的排序
//something
}
void cdq(int l, int r) {//这里的区间是左闭右开,因为这样可以很容易的取到 mid
if (l + 1 == r)
return ;
cdq(l, mid);//先搞左子区间
sort(val + l, val + mid, cmp2);
sort(val + mid, val + r, cmp2);//先对左右子区间排序
int pos = l;
for (int i = mid; i < r; i++) {
for (; pos < mid && /*对应偏序满足*/; pos++) /*更新数据*/;
/*[l,pos] 向 i 贡献(查询数据结构)*/
}
for (int i = l; i < pos; i++) /*数据还原*/;
copy(ori + l, ori + r, val + l);
cdq(mid, r);//再搞右子区间
}
sort(val + 1, val + n + 1, cmp1);//排序
copy(val + 1, val + n + 1, ori + 1);//记录原始顺序
cdq(1, n + 1);//cdq 分治
牢记 cdq 五字口诀:
“左(计算左子区间),排(排序),算(计算这个区间的答案),还(还原),右(计算右子区间)”。
三位偏序代码
注意一个很大的坑点:这里的数据会出现重复,而这些重复的元素之间可以互相贡献,不能直接 cdq 分治,需要去重!!!
#include <bits/stdc++.h>
#define int long long
#define mid ((l + r) >> 1)
using namespace std;
const int N = 200010;
struct node {
int id, a, b, c;
} val[N], ori[N];
int sum[N], num[N], ans[N];
int n, k;
bool cmp1(node x, node y) {
if (x.a != y.a)
return x.a < y.a;
if (x.b != y.b)
return x.b < y.b;
return x.c < y.c;
}
bool cmp2(node x, node y) {
return x.b < y.b;
}
struct BIT {
int tree[N];
void add(int pos, int val) {
for (; pos <= 200000; pos += pos & -pos)
tree[pos] += val;
}
int query(int pos) {
int ans = 0;
for (; pos; pos -= pos & -pos)
ans += tree[pos];
return ans;
}
} wsx;
void cdq(int l, int r) {
if (l + 1 == r)
return ;
cdq(l, mid);
sort(val + l, val + mid, cmp2);
sort(val + mid, val + r, cmp2);
int pos = l;
for (int i = mid; i < r; i++) {
for (; pos < mid && val[pos].b <= val[i].b; pos++)
wsx.add(val[pos].c, num[val[pos].id]);
sum[val[i].id] += wsx.query(val[i].c);
}
for (int i = l; i < pos; i++)
wsx.add(val[i].c, -num[val[i].id]);
copy(ori + l, ori + r, val + l);
cdq(mid, r);
}
signed main() {
cin >> n >> k;
for (int i = 1; i <= n; i++) {
cin >> val[i].a >> val[i].b >> val[i].c;
val[i].id = i, num[i] = 1;
}
sort(val + 1, val + n + 1, cmp1);
int cnt = 1;
for (int i = 2; i <= n; i++)
if (val[i].a == val[cnt].a && val[i].b == val[cnt].b && val[i].c == val[cnt].c)
num[val[cnt].id]++;
else
val[++cnt] = val[i];
copy(val + 1, val + cnt + 1, ori + 1);
cdq(1, cnt + 1);
for (int i = 1; i <= cnt; i++)
ans[sum[val[i].id] + num[val[i].id] - 1] += num[val[i].id];
for (int i = 0; i < n; i++)
cout << ans[i] << endl;
return 0;
}
cdq 时间复杂度
很显然外面有一个分治的层数,也就是 O ( log n ) O(\log n) O(logn),这是比较显然的。
然后观察每一个函数处理里面有哪些比较耗费时间的操作,显然就是排序和计算答案的部分。
每一层排序的合起来就是 O ( n log 2 n ) O(n \log^2 n) O(nlog2n),然后计算答案的就是 O ( n A ) O(nA) O(nA),其中 A A A 是数据结构维护的开销。例如上一道题的三维偏序就是 A = log n A = \log n A=logn,将 A A A 代入就可以发现时间复杂度是有两个 $\log $。
综上,cdq 分治的时间复杂度就是 O ( log n × ( n log n + n × A ) ) O(\log n \times (n \log n + n \times A)) O(logn×(nlogn+n×A))。
关于模板的问题
观察模板的处理顺序,容易发现是先处理左子区间,再计算整个区间的答案,再计算右子区间。
那我们可不可以不使用这种中序遍历的方式,而是使用类似后序遍历或者是先序遍历的顺序呢?
答案是,不可以!!!原因很简单,当 sort 做完后,数组内的元素就不是按第一个偏序关系(cmp1)有序的了,就会导致后续处理右半部分时不满足第一个偏序关系的前置条件,得到错误答案。
所以就只能使用中序遍历的方法了,正确性显然。而且这样代码逻辑较简单,很容易写。
cdq 分治优化 dp
这下我们不讲题了,因为没有一道题是完全基础的,都需要加上一堆黑暗料理才能通过。这里就直接丢一道题:
给定一个序列,找到一个最长子序列,使得对于子序列中的任意 j < i j<i j<i 满足:
- a j ≤ a i a_j \le a_i aj≤ai
- b j ≤ b i b_j \le b_i bj≤bi
这就是一个 LIS 的改编版。
这个东西其实很显然就可以写出 O ( n 2 ) O(n^2) O(n2) 的暴力 dp。直接使用类似 LIS 的转移即可:
d p i = max { d p j + ( j < i and a j ≤ a i and b j ≤ b i ) } dp_i = \max\{dp_j+(j<i \ \text{and} \ a_j \le a_i \ \text{and} \ b_j \le b_i)\} dpi=max{dpj+(j<i and aj≤ai and bj≤bi)}
然后,你就可以发现一些比较有乐趣的事情,请问: ( j < i and a j ≤ a i and b j ≤ b i ) (j<i \ \text{and} \ a_j \le a_i \ \text{and} \ b_j \le b_i) (j<i and aj≤ai and bj≤bi) 这个东西是什么?
这不就是三维偏序吗!
我们会思考:欸,既然三维偏序是 cdq 最基础的应用,那我们可不可以也用 cdq 分治来优化这个 dp 呢?
我们不妨来试一下。
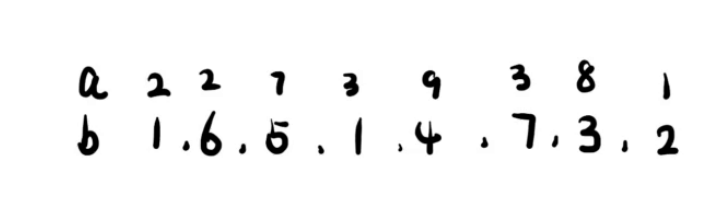
不妨是这个例子。模拟就可以发现,我们的确可以使用三位偏序的方式来优化这个 dp。
cdq 对时间分治(修改 / 查询类问题)
有时候我们会遇到一些经典问题:有一堆修改,有一堆查询,查询和修改是交替的,还需要你处理所有的操作。
一般来说我们都是想的毒瘤 DS,但是有些时候 cdq 分治也可以做。
cdq 是这样做的:将这种动态的问题,转化为静态的问题来解决。
我们很容易想到考虑这件事:每一个修改,它到底会影响到哪一个查询。
可以这样做:对于某一个查询,看一看那些修改对这个查询起作用,算一下每一个修改对这个查询的贡献。
因为对查询起作用的修改是一个区间的形式,所以可以使用 cdq 分治。
每一次可以计算左半边的贡献和右半边的贡献,最终合起来就可以得到整个区间的贡献,也就可以求解查询了。所以 cdq 分治在这里是正确性显然的。至于怎么写就是另一个故事了。





















 761
761

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








