HTML数据可视化散点图,一维数据可视化：散点图(dot plot)

在统计分析过程中，有时需要对一维数据(单变量数据)进行可视化，以方便观察数据点分布的特征，并提出基于直观感受的预测。

一维数据

一维数据(单变量数据)，顾名思义，就是可以用一个变量来表示的数据集。比如，对CPU的使用率进行随机采样所得到的数据集就是一维数据：

//一维数据示例，CPU使用率

27, 22, 30, 30, 25, 28, 28, 30, 78, 88, 86, 29, 17, 19, 23, 26, 27, 30, 31, 27

散点图

对于一维数据，可以通过散点图来进行可视化。所谓散点图，就是把所有的数据点都描绘在一条直线上(一般使用水平直线)，数据点的值决定其在直线上的位置。以上述CPU使用率数据为例，下面就是该数据的散点图：

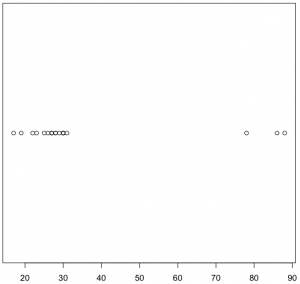
可以观察到，CPU数据聚集在30附近，并在接近90的地方有几个离散点。

上面的散点图有个问题：数据聚集的地方无法清晰地分辨出聚集程度，而值相同的数据点则会互相遮蔽从而引起误解。

对于散点图的这个问题，一个解决方案是将数据点进行分离，比如将值相同的数据点进行层叠：

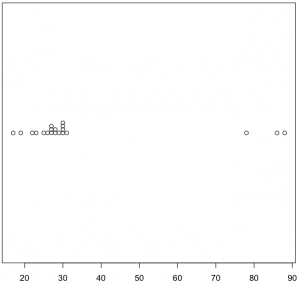
可以看到，与之前的散点图相比，数据点分离后的散点图更容易分辨聚集程度。

另一个解决方案则是对所有的散点进行随机离散化(抖动图 jitter plot)：