java 欧拉工程_Java进阶之欧拉工程 第十五篇【网格路径问题】

网格路径问题，中文翻译如下：

从 2

2的格子的左上角开始，只允许向右和向下移动，一共有六种路径可以抵达右下角

那么在20

20的路径中一共有多少条这样的路径？

原题如下：

Starting in the top left corner of a 2

2 grid,

and only being able to move to the right and down, there are exactly 6 routes to the bottom right corner.

How many such routes are there through a 20

20

grid?

解题思路：

以以上的2X2的格子为例，从起点到达最左边一竖排    ↓

和最上面一横排——>所有的点的路径都为1，其余所有点的到达路径都可以看作左边相邻的点的路径数加上上方相邻点的路径和，这样说起来比较抽象，让我来画一个示意图吧：

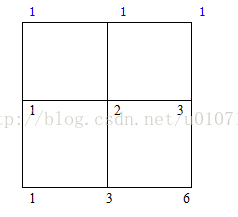
这样就很清晰了，对于20X20的表格，其实它的节点正好可以可以做一个21X21的数组，然后通过遍历依次对节点的路径数赋值，最后得到右下角节点的路径数，java代码如下：

public static void main(String[] args) {

// TODO Auto-generated method stub

long[][] jiedian= new long[21][21];

//在节点便历之前必须先对边线上的节点进行赋值

for(int i=0;i<21;i++){

for(int j=0;j<21;j++){

jiedian[0][j]=1;

jiedian[i][0]=1;

}

}

for(int m=1;m<21;m++){

for(int n=1;n<21;n++){

jiedian[m][n]=jiedian[m-1][n]+jiedian[m][n-1];

}

}

System.out.println(jiedian[20][20]);

}

}

原文：http://blog.youkuaiyun.com/u010717556/article/details/38658969