目录
逐渐改进,从各向同性到VTI各向异性(前面的帖子有各向同性和VTI的程序,基础程序可以参考我前面的帖子),再到TTI介质,实际上只是刚度系数矩阵换了换而已。下面给出很多模拟的例子,可以参考。在这里强调几项关键问题,适用于ISO,VTI,TTI介质。
一. 关键问题
1. 稳定性和频散
波动方程有限差分法模拟最关键的两大问题是稳定性和频散问题,有关稳定性条件和频散关系的研究,国内董良国教授在2000年左右做过详细的研究,有关细节搜索文章阅读即可。粗略地讲:
其中稳定性条件:V*dt/dx<阈值,阈值在0.541(2N=10阶空间差分精度)-- 0.707(2N=2阶空间差分精度)之间;V为模型的最大速度,dt, dx分别为时间和空间的采样间距。速度越高越不稳定。
频散:dx/λ。λ为波长,主频越低,波长越长, 该项越小,越不容易发生频散。
2. 震源的设置
Txx和Tzz同时施加震源,相当于炸药震源(纯P),产生的主要是P波。
Vz上施加震源,相当于垂向重锤激发,同时产生P和S波。
3. 弹性波 -> 拟声波、声波的转换
按照Alkhalifah(2000)文章的推导,拟声波只是将Vs强制置零。此时各向异性计算的拟声波场中会出现一些S波的残留波场(泄漏),只需要在震源附近填充一点各向同性层即可消除伪影,只保留声波的部分。
强制Vs等于零后,δ>epsilon时,稳定性很差。
Vs, epsilon, δ都置零后,就是各向同性声波波场。
4. PML边界
PML边界目前处于内置状态,外置PML的程序在最下面。后面给出了一系列数值算例,不懂的欢迎随时交流。
二. 原理




三. 代码
3.1 C/C++代码
这里提供的是C/C++版本的代码,MATLAB版本的代码在下面。
/****************************************************************************************/
/***********Elastic Velocity-Stress Finite-difference Modeling with PML**********/
/*************High Order (Highest: sixteen order) Finite-difference****************/
/***************************Written By Zhang Jianming,2022.10.10****************/
/***************************************CopyRight************************************/
#include<stdio.h>
#include<math.h>
#include<iostream>
#include<fstream>
#include<iomanip>
using namespace std;
#define PI 3.1415926
#define dx 10
#define dz 10
#define NX 1000
#define NZ 1000
#define NT 10001
#define dt 0.0005
#define N 6
#define pml 50
float fi=0*(PI/4.0);
int main()
{
//cout<<"sin(pi/6)="<<sin(PI/6)<<endl;
float **Txx=new float*[NX],**Txx_x=new float*[NX],**Txx_z=new float*[NX];
float **Tzz=new float*[NX],**Tzz_x=new float*[NX],**Tzz_z=new float*[NX];
float **Txz=new float*[NX],**Txz_x=new float*[NX],**Txz_z=new float*[NX];
float **Vx=new float*[NX],**Vx_x=new float*[NX],**Vx_z=new float*[NX];
//A wierd question: icpc compeler broke down using the below Vz, why?
float **Vz=new float*[NX],**Vz_x=new float*[NX],**Vz_z=new float*[NX];
float **L=new float*[NX],**M=new float*[NX],**e=new float*[NX];
float **C11=new float*[NX],**C33=new float*[NX],**C44=new float*[NX],**C66=new float*[NX],**C13=new float*[NX],**Rou=new float*[NX];
float **C_11=new float*[NX],**C_13=new float*[NX],**C_15=new float*[NX],**C_33=new float*[NX],**C_35=new float*[NX],**C_55=new float*[NX],**O=new float*[NX];
float **Vp=new float*[NX],**Eps=new float*[NX],**Del=new float*[NX],**Vs=new float*[NX],**Gam=new float*[NX],**F=new float*[NX];
float **data_vx=new float*[NX],**data_vz=new float*[NX];//Observed Vx and Vz components
for(int i=0;i<NX;i++)
{
Txx[i]=new float[NZ];Txx_x[i]=new float[NZ];Txx_z[i]=new float[NZ];
Tzz[i]=new float[NZ];Tzz_x[i]=new float[NZ];Tzz_z[i]=new float[NZ];
Txz[i]=new float[NZ];Txz_x[i]=new float[NZ];Txz_z[i]=new float[NZ];
Vx[i]=new float[NZ];Vx_x[i]=new float[NZ];Vx_z[i]=new float[NZ];
Vz[i]=new float[NZ];Vz_x[i]=new float[NZ];Vz_z[i]=new float[NZ];
L[i]=new float[NZ];M[i]=new float[NZ];e[i]=new float[NZ];
C11[i]=new float[NZ];C33[i]=new float[NZ];C44[i]=new float[NZ];C66[i]=new float[NZ];C13[i]=new float[NZ];Rou[i]=new float[NZ];
Vp[i]=new float[NZ];Eps[i]=new float[NZ];Del[i]=new float[NZ];Vs[i]=new float[NZ];Gam[i]=new float[NZ];F[i]=new float[NZ];
C_11[i]=new float[NZ];C_13[i]=new float[NZ];C_15[i]=new float[NZ];C_33[i]=new float[NZ];C_35[i]=new float[NZ];C_55[i]=new float[NZ];O[i]=new float[NZ];
for(int j=0;j<NZ;j++)
{
Txx[i][j]=0;Txx_x[i][j]=0;Txx_z[i][j]=0;
Tzz[i][j]=0;Tzz_x[i][j]=0;Tzz_z[i][j]=0;
Txz[i][j]=0;Txz_x[i][j]=0;Txz_z[i][j]=0;
Vx[i][j]=0;Vx_x[i][j]=0;Vx_z[i][j]=0;
Vz[i][j]=0;Vz_x[i][j]=0;Vz_z[i][j]=0;
}
data_vx[i]=new float[NT];data_vz[i]=new float[NT];
for(int j=0;j<NT;j++)
{
data_vx[i][j]=0;
data_vz[i][j]=0;
}
}
///*
//FILE *filename;
//filename=fopen("mar_140_501_h15s","rb");
//for(int i=0;i<NX;i++)
// for(int j=0;j<NZ;j++)
// fread(&Vp[i][j], sizeof(float), 1, filename);
//fclose(filename);
//*/
int i,j,k,f0=15;float t0=1.2/f0;
int SX=NX/2;int SZ=NZ/2;
//int SX=2*pml;int SZ=2*pml;
FILE *fp1,*fp11,*fp12,*fp2,*fp3,*fp4,*fp5,*fp6,*fp7;
float ddx[NX][NZ];float ddz[NX][NZ];
float R=0.001,Vmax=7500;
int x,z,plx,plz;
for(i=0;i<NX;i++)
for(j=0;j<NZ;j++)
{
//Iso
//L[i][j]=1.19*pow(10, 10);M[i][j]=5.4*pow(10, 9);e[i][j]=2.0*pow(10, 3);
//C11[i][j]=L[i][j]+2*M[i][j];
//C33[i][j]=C11[i][j];
//C44[i][j]=M[i][j];
//C66[i][j]=M[i][j];
//C13[i][j]=L[i][j];
//Rou[i][j]=e[i][j];
//Ice
//C11[i][j]=13.33*pow(10, 9);
//C33[i][j]=14.28*pow(10, 9);
//C44[i][j]=3.26*pow(10, 9);
//C66[i][j]=3.65*pow(10, 9);
//C13[i][j]=5.08*pow(10, 9);
//Rou[i][j]=0.91*pow(10, 3);
//Quartz
//C11[i][j]=116.6*pow(10, 9);
//C33[i][j]=110.40*pow(10, 9);
//C44[i][j]=36.06*pow(10, 9);
//C66[i][j]=49.95*pow(10, 9);
//C13[i][j]=32.8*pow(10, 9);
//Rou[i][j]=2.65*pow(10, 3);
//Mantle
//C11[i][j]=212.8*pow(10, 9);
//C33[i][j]=249.18*pow(10, 9);
//C44[i][j]=70.47*pow(10, 9);
//C66[i][j]=66.72*pow(10, 9);
//C13[i][j]=76.24*pow(10, 9);
//Rou[i][j]=3.22*pow(10, 3);
//Ref
//C11[i][j]=25.5*pow(10, 9);
//C33[i][j]=18.4*pow(10, 9);
//C44[i][j]=5.6*pow(10, 9);
//C66[i][j]=5.6*pow(10, 9);
//C13[i][j]=10.4*pow(10, 9);
//Rou[i][j]=2.44*pow(10, 3);
//Thomsen
Vp[i][j]=3000;
Eps[i][j]=0.0;
Del[i][j]=0.0;
Vs[i][j]=2000;//Vp[i][j]/sqrt(3);
Gam[i][j]=0.1;
if(j>7.0/10.0*NZ)
//if(j>-200*i/1000.0+800)
//if(j>-100*cos(2*PI*i/500.0)+700)
{
//Vp[i][j]=4000;
Vs[i][j]=2800;
//Vs[i][j]=2800;
}
if(j>8.0/10.0*NZ)
{
Vp[i][j]=4000;
//Vs[i][j]=2800;
}
//if(j>80) {Vp[i][j]=1000;Vs[i][j]=800;}
Rou[i][j]=3.44*pow(10, 3);
C11[i][j]=Rou[i][j]*(1.0+2*Eps[i][j])*pow(Vp[i][j],2);
C33[i][j]=Rou[i][j]*pow(Vp[i][j],2);
C44[i][j]=Rou[i][j]*pow(Vs[i][j],2);
C66[i][j]=Rou[i][j]*(1.0+2*Gam[i][j])*pow(Vs[i][j],2);
F[i][j]=1.0-pow(Vs[i][j],2)/pow(Vp[i][j],2);
C13[i][j]=Rou[i][j]*pow(Vp[i][j],2)*sqrt(F[i][j]*(F[i][j]+2*Del[i][j]))-Rou[i][j]*pow(Vs[i][j],2);
O[i][j]=fi;
C_11[i][j]=C11[i][j]*pow(cos(O[i][j]),4)+C33[i][j]*pow(sin(O[i][j]),4)+(2*C13[i][j]+4*C44[i][j])*pow(sin(O[i][j]),2)*pow(cos(O[i][j]),2);
C_13[i][j]=(C11[i][j]+C33[i][j]-4*C44[i][j])*pow(sin(O[i][j]),2)*pow(cos(O[i][j]),2)+C13[i][j]*(pow(sin(O[i][j]),4)+pow(cos(O[i][j]),4));
C_15[i][j]=(C13[i][j]-C11[i][j]+2*C44[i][j])*pow(sin(O[i][j]),1)*pow(cos(O[i][j]),3)-(C13[i][j]-C33[i][j]+2*C44[i][j])*pow(sin(O[i][j]),3)*pow(cos(O[i][j]),1);
C_33[i][j]=C11[i][j]*pow(sin(O[i][j]),4)+C33[i][j]*pow(cos(O[i][j]),4)+(2*C13[i][j]+4*C44[i][j])*pow(sin(O[i][j]),2)*pow(cos(O[i][j]),2);
C_35[i][j]=(C13[i][j]-C11[i][j]+2*C44[i][j])*pow(sin(O[i][j]),3)*pow(cos(O[i][j]),1)-(C13[i][j]-C33[i][j]+2*C44[i][j])*pow(sin(O[i][j]),1)*pow(cos(O[i][j]),3);
C_55[i][j]=(C11[i][j]+C33[i][j]-2*C13[i][j])*pow(sin(O[i][j]),2)*pow(cos(O[i][j]),2)+C44[i][j]*pow(pow(cos(O[i][j]),2)-pow(sin(O[i][j]),2),2);
}
//PML
plx=pml*dx;plz=pml*dz;
for(i=0;i<NX;i++)
for(j=0;j<NZ;j++)
{
if(i>=0&&i<pml&&j>=0&&j<pml)
{
x=pml-i;z=pml-j;
ddx[i][j]=-log(R)*3*Vmax*x*x/(2*plx*plx);
ddz[i][j]=-log(R)*3*Vmax*z*z/(2*plz*plz);
}
else if(i>=0&&i<pml&&j>NZ-pml&&j<NZ)
{
x=pml-i;z=j-(NZ-pml);
ddx[i][j]=-log(R)*3*Vmax*x*x/(2*plx*plx);
ddz[i][j]=-log(R)*3*Vmax*z*z/(2*plz*plz);
}
else if(i>NX-pml&&i<NX&&j>=0&&j<pml)
{
x=i-(NX-pml);z=pml-j;
ddx[i][j]=-log(R)*3*Vmax*x*x/(2*plx*plx);
ddz[i][j]=-log(R)*3*Vmax*z*z/(2*plz*plz);
}
else if(i>NX-pml&&i<NX&&j>NZ-pml&&j<NZ)
{
x=i-(NX-pml);z=j-(NZ-pml);
ddx[i][j]=-log(R)*3*Vmax*x*x/(2*plx*plx);
ddz[i][j]=-log(R)*3*Vmax*z*z/(2*plz*plz);
}
else if(i>=pml&&i<=NX-pml&&j>=0&&j<pml)
{
x=i-pml;z=pml-j;
ddx[i][j]=0;
ddz[i][j]=-log(R)*3*Vmax*z*z/(2*plz*plz);
}
else if(i>=pml&&i<=NX-pml&&j>NZ-pml&&j<NZ)
{
x=i-pml;z=j-(NZ-pml);
ddx[i][j]=0;
ddz[i][j]=-log(R)*3*Vmax*z*z/(2*plz*plz);
}
else if(i>=0&&i<pml&&j>=pml&&j<=NZ-pml)
{
x=pml-i;z=j-pml;
ddx[i][j]=-log(R)*3*Vmax*x*x/(2*plx*plx);
ddz[i][j]=0;
}
else if(i>NX-pml&&i<NX&&j>=pml&&j<=NZ-pml)
{
x=i-(NX-pml);z=j-pml;
ddx[i][j]=-log(R)*3*Vmax*x*x/(2*plx*plx);
ddz[i][j]=0;
}
else if(i>=pml&&i<=NX-pml&&j>=pml&&j<=NZ-pml)
{
x=i-pml;z=j-pml;
ddx[i][j]=0;
ddz[i][j]=0;
}
}
float cof[N];
if(N==1)
{ cof[0]=1.0;}
if(N==2)
{ cof[0]=1.125;cof[1]=-0.041666667;}
if(N==3)
{ cof[0]=1.171875;cof[1]=-0.065104167;cof[2]=0.0046875;}
if(N==4)
{ cof[0]=1.196289;cof[1]=-0.0797526;cof[2]=0.009570313;cof[3]=-0.0006975447;}
if(N==5)
{ cof[0]=1.2112427;cof[1]=-0.08972168;cof[2]=0.013842773;cof[3]=-0.0017656599;cof[4]=0.00011867947;}
if(N==6)
{ cof[0]=1.2213364;cof[1]=-0.096931458;cof[2]=0.017447662;cof[3]=-0.0029672895;cof[4]=0.00035900540;cof[5]=-0.000021847812;}
if(N==7)
{ cof[0]=1.2286062;cof[1]=-0.10238385;cof[2]=0.02047677;cof[3]=-0.0041789327;cof[4]=0.00068945355;cof[5]=-0.000076922503;cof[6]=0.0000042365148;}
if(N==8)
{ cof[0]=1.2340911;cof[1]=-0.10664985;cof[2]=0.023036367;cof[3]=-0.0053423856;cof[4]=0.0010772712;cof[5]=-0.00016641888;cof[6]=0.000017021711;cof[7]=-0.00000085234642;}
for(k=0;k<NT;k++)
{
for(i=N;i<NX-N;i++)
{
for(j=N;j<NZ-N;j++)
{
//high order TTI
float pxVx=0;float pzVx=0;float pxVz=0;float pzVz=0;
for(int in=0;in<N;in++)
{
pxVx+=cof[in]*(Vx[i+in+1][j]-Vx[i-in][j]);
pxVz+=cof[in]*(Vz[i+in][j]-Vz[i-in-1][j]);
pzVx+=cof[in]*(Vx[i][j+in+1]-Vx[i][j-in]);
pzVz+=cof[in]*(Vz[i][j+in]-Vz[i][j-in-1]);
}
Txx_x[i][j]=1.0/(1+0.5*dt*ddx[i][j])*((1-0.5*ddx[i][j]*dt)*Txx_x[i][j]+C_11[i][j]*dt/dx*pxVx+C_15[i][j]*dt/dx*pxVz);
Txx_z[i][j]=1.0/(1+0.5*dt*ddz[i][j])*((1-0.5*ddz[i][j]*dt)*Txx_z[i][j]+C_13[i][j]*dt/dz*pzVz+C_15[i][j]*dt/dz*pzVx);
Tzz_x[i][j]=1.0/(1+0.5*dt*ddx[i][j])*((1-0.5*ddx[i][j]*dt)*Tzz_x[i][j]+C_13[i][j]*dt/dx*pxVx+C_35[i][j]*dt/dx*pxVz);
Tzz_z[i][j]=1.0/(1+0.5*dt*ddz[i][j])*((1-0.5*ddz[i][j]*dt)*Tzz_z[i][j]+C_33[i][j]*dt/dz*pzVz+C_35[i][j]*dt/dz*pzVx);
Txx[i][j]=Txx_x[i][j]+Txx_z[i][j];
Tzz[i][j]=Tzz_x[i][j]+Tzz_z[i][j];
if(i==SX&&j==SZ)
{
float tmp=pow(PI*f0*(k*dt-t0),2);
//Ricker
Txx_x[i][j]+=1*exp(-1.0*tmp)*(1-2.0*tmp);
Txx_z[i][j]+=1*exp(-1.0*tmp)*(1-2.0*tmp);
Tzz_x[i][j]+=1*exp(-1.0*tmp)*(1-2.0*tmp);
Tzz_z[i][j]+=1*exp(-1.0*tmp)*(1-2.0*tmp);
//Gauss
//Tzz[i][j]+=-1.0*PI*PI*f0*f0*(k*dt-t0)*exp(-1.0*tmp)*(3.0-2.0*tmp);
//Txx[i][j]+=-1.0*PI*PI*f0*f0*(k*dt-t0)*exp(-1.0*tmp)*(3.0-2.0*tmp);
}
pxVx=0;pzVx=0;pxVz=0;pzVz=0;
for(int in=0;in<N;in++)
{
pxVx+=cof[in]*(Vx[i+in+1][j]-Vx[i-in][j]);
pxVz+=cof[in]*(Vz[i+in][j]-Vz[i-in-1][j]);
pzVx+=cof[in]*(Vx[i][j+in+1]-Vx[i][j-in]);
pzVz+=cof[in]*(Vz[i][j+in]-Vz[i][j-in-1]);
}
Txz_x[i][j]=1.0/(1+0.5*dt*ddx[i][j])*((1-0.5*ddx[i][j]*dt)*Txz_x[i][j]+C_15[i][j]*dt/dx*pxVx+C_55[i][j]*dt/dx*pxVz);
Txz_z[i][j]=1.0/(1+0.5*dt*ddz[i][j])*((1-0.5*ddz[i][j]*dt)*Txz_z[i][j]+C_35[i][j]*dt/dz*pzVz+C_55[i][j]*dt/dz*pzVx);
Txz[i][j]=Txz_x[i][j]+Txz_z[i][j];
}
}
for(i=N;i<NX-N;i++)
{
for(j=N;j<NZ-N;j++)
{
float pxTxx=0;float pzTxz=0;
for(int in=0;in<N;in++)
{
pxTxx+=cof[in]*(Txx[i+in][j]-Txx[i-in-1][j]);
pzTxz+=cof[in]*(Txz[i][j+in]-Txz[i][j-in-1]);
}
Vx_x[i][j]=1.0/(1+0.5*dt*ddx[i][j])*((1-0.5*ddx[i][j]*dt)*Vx_x[i][j]+dt/Rou[i][j]/dx*pxTxx);
Vx_z[i][j]=1.0/(1+0.5*dt*ddz[i][j])*((1-0.5*ddz[i][j]*dt)*Vx_z[i][j]+dt/Rou[i][j]/dz*pzTxz);
Vx[i][j]=Vx_x[i][j]+Vx_z[i][j];
//if(i==SX&&j==SZ)
//{
// float tmp=pow(PI*f0*(k*dt-t0),2);
// //Ricker
// Vz_x[i][j]+=1*exp(-1.0*tmp)*(1-2.0*tmp);
// Vz_z[i][j]+=1*exp(-1.0*tmp)*(1-2.0*tmp);
//}
float pxTxz=0;float pzTzz=0;
for(int in=0;in<N;in++)
{
pxTxz+=cof[in]*(Txz[i+in+1][j]-Txz[i-in][j]);
pzTzz+=cof[in]*(Tzz[i][j+in+1]-Tzz[i][j-in]);
}
Vz_x[i][j]=1.0/(1+0.5*dt*ddx[i][j])*((1-0.5*ddx[i][j]*dt)*Vz_x[i][j]+dt/Rou[i][j]/dx*pxTxz);
Vz_z[i][j]=1.0/(1+0.5*dt*ddz[i][j])*((1-0.5*ddz[i][j]*dt)*Vz_z[i][j]+dt/Rou[i][j]/dz*pzTzz);
Vz[i][j]=Vz_x[i][j]+Vz_z[i][j];
}
}
for (i = 0; i < NX; i++)
{
int rz=SZ;
data_vx[i][k]=Vx[i][rz];
data_vz[i][k]=Vz[i][rz];
}
if(k%1000==0)
{
//FILE *fp121;
//char name[256];
//sprintf(name,"T_TTI2.dat%d",k);
//fp121=fopen(name, "wb+");
//for (i = 0; i < NX; i++)
// for (j = 0; j < NZ; j++)
// {
// float T=1.0/2*(Txx[i][j]+Tzz[i][j]);
// fwrite(&T, sizeof(float), 1, fp121);
// }
//fclose(fp121);
FILE *fp122;
char name[256];
sprintf(name,"Vx.dat%d",k);
fp122=fopen(name, "wb+");
for (i = 0; i < NX; i++)
for (j = 0; j < NZ; j++)
{
fwrite(&Vx[i][j], sizeof(float), 1, fp122);
}
fclose(fp122);
FILE *fp123;
sprintf(name,"Vz.dat%d",k);
fp123=fopen(name, "wb+");
for (i = 0; i < NX; i++)
for (j = 0; j < NZ; j++)
{
fwrite(&Vz[i][j], sizeof(float), 1, fp123);
}
fclose(fp123);
}
}
fp1=fopen("Txx.dat", "wb+");
for (i = 0; i < NX; i++)
for (j = 0; j < NZ; j++)
{
fwrite(&Txx[i][j], sizeof(float), 1, fp1);
}
fp2=fopen("Tzz.dat", "wb+");
for (i = 0; i < NX; i++)
for (j = 0; j < NZ; j++)
{
fwrite(&Tzz[i][j], sizeof(float), 1, fp2);
}
fp12=fopen("T.dat", "wb+");
for (i = 0; i < NX; i++)
for (j = 0; j < NZ; j++)
{
float T=1.0/2*(Txx[i][j]+Tzz[i][j]);
fwrite(&T, sizeof(float), 1, fp12);
}
fp3=fopen("Txz.dat", "wb+");
for (i = 0; i < NX; i++)
for (j = 0; j < NZ; j++)
{
fwrite(&Txz[i][j], sizeof(float), 1, fp3);
}
fp4=fopen("Vx.dat", "wb+");
for (i = 0; i < NX; i++)
for (j = 0; j < NZ; j++)
{
fwrite(&Vx[i][j], sizeof(float), 1, fp4);
}
fp5=fopen("Vz.dat", "wb+");
for (i = 0; i < NX; i++)
for (j = 0; j < NZ; j++)
{
fwrite(&Vz[i][j], sizeof(float), 1, fp5);
}
fp6=fopen("data_vx.dat", "wb+");
for (i = 0; i < NX; i++)
for (j = 0; j < NT; j++)
{
fwrite(&data_vx[i][j], sizeof(float), 1, fp6);
}
fp7=fopen("data_vz.dat", "wb+");
for (i = 0; i < NX; i++)
for (j = 0; j < NT; j++)
{
fwrite(&data_vz[i][j], sizeof(float), 1, fp7);
}
fp1=fopen("Vp.dat", "wb+");
for (i = 0; i < NX; i++)
for (j = 0; j < NZ; j++)
{
fwrite(&Vp[i][j], sizeof(float), 1, fp1);
}
//We should delete memory here!!!
}3.2 MATLAB代码
% Elastic Velocity-Stress Finite-difference Modeling with PML in MATLAB
% Converted from C++ code provided by Zhang Jianming
% Constants
PI = 3.1415926;
dx = 10;
dz = 10;
NX = 400;
NZ = 400;
NT = 1001;
dt = 0.0005;
N = 6;
pml = 5;
fi = (PI / 4.0);
% Allocate memory for matrices
Txx = zeros(NX, NZ);
Txx_x = zeros(NX, NZ);
Txx_z = zeros(NX, NZ);
Tzz = zeros(NX, NZ);
Tzz_x = zeros(NX, NZ);
Tzz_z = zeros(NX, NZ);
Txz = zeros(NX, NZ);
Txz_x = zeros(NX, NZ);
Txz_z = zeros(NX, NZ);
Vx = zeros(NX, NZ);
Vx_x = zeros(NX, NZ);
Vx_z = zeros(NX, NZ);
Vz = zeros(NX, NZ);
Vz_x = zeros(NX, NZ);
Vz_z = zeros(NX, NZ);
L = zeros(NX, NZ);
M = zeros(NX, NZ);
e = zeros(NX, NZ);
C11 = zeros(NX, NZ);
C33 = zeros(NX, NZ);
C44 = zeros(NX, NZ);
C66 = zeros(NX, NZ);
C13 = zeros(NX, NZ);
Rou = zeros(NX, NZ);
C_11 = zeros(NX, NZ);
C_13 = zeros(NX, NZ);
C_15 = zeros(NX, NZ);
C_33 = zeros(NX, NZ);
C_35 = zeros(NX, NZ);
C_55 = zeros(NX, NZ);
O = zeros(NX, NZ);
Vp = zeros(NX, NZ);
Eps = zeros(NX, NZ);
Del = zeros(NX, NZ);
Vs = zeros(NX, NZ);
Gam = zeros(NX, NZ);
F = zeros(NX, NZ);
data_vx = zeros(NX, NT);
data_vz = zeros(NX, NT);
% Initialize parameters
f0 = 15;
t0 = 1.2 / f0;
SX = floor(NX / 2);
SZ = floor(NZ / 2);
R = 0.001;
Vmax = 7500;
plx = pml * dx;
plz = pml * dz;
ddx = zeros(NX, NZ);
ddz = zeros(NX, NZ);
% Initialize model parameters
for i = 1:NX
for j = 1:NZ
Vp(i, j) = 3000;
Eps(i, j) = 0.4;
Del(i, j) = 0.2;
Vs(i, j) = 2000;
Gam(i, j) = 0.1;
%
% if j > 7.0 / 10.0 * NZ
% Vs(i, j) = 2800;
% end
%
% if j > 8.0 / 10.0 * NZ
% Vp(i, j) = 4000;
% end
%
Rou(i, j) = 3.44 * 10^3;
C11(i, j) = Rou(i, j) * (1.0 + 2 * Eps(i, j)) * Vp(i, j)^2;
C33(i, j) = Rou(i, j) * Vp(i, j)^2;
C44(i, j) = Rou(i, j) * Vs(i, j)^2;
C66(i, j) = Rou(i, j) * (1.0 + 2 * Gam(i, j)) * Vs(i, j)^2;
F(i, j) = 1.0 - Vs(i, j)^2 / Vp(i, j)^2;
C13(i, j) = Rou(i, j) * Vp(i, j)^2 * sqrt(F(i, j) * (F(i, j) + 2 * Del(i, j))) - Rou(i, j) * Vs(i, j)^2;
O(i, j) = fi;
C_11(i, j) = C11(i, j) * cos(O(i, j))^4 + C33(i, j) * sin(O(i, j))^4 + (2 * C13(i, j) + 4 * C44(i, j)) * sin(O(i, j))^2 * cos(O(i, j))^2;
C_13(i, j) = (C11(i, j) + C33(i, j) - 4 * C44(i, j)) * sin(O(i, j))^2 * cos(O(i, j))^2 + C13(i, j) * (sin(O(i, j))^4 + cos(O(i, j))^4);
C_15(i, j) = (C13(i, j) - C11(i, j) + 2 * C44(i, j)) * sin(O(i, j)) * cos(O(i, j))^3 - (C13(i, j) - C33(i, j) + 2 * C44(i, j)) * sin(O(i, j))^3 * cos(O(i, j));
C_33(i, j) = C11(i, j) * sin(O(i, j))^4 + C33(i, j) * cos(O(i, j))^4 + (2 * C13(i, j) + 4 * C44(i, j)) * sin(O(i, j))^2 * cos(O(i, j))^2;
C_35(i, j) = (C13(i, j) - C11(i, j) + 2 * C44(i, j)) * sin(O(i, j))^3 * cos(O(i, j)) - (C13(i, j) - C33(i, j) + 2 * C44(i, j)) * sin(O(i, j)) * cos(O(i, j))^3;
C_55(i, j) = (C11(i, j) + C33(i, j) - 2 * C13(i, j)) * sin(O(i, j))^2 * cos(O(i, j))^2 + C44(i, j) * (cos(O(i, j))^2 - sin(O(i, j))^2)^2;
end
end
% PML setup
for i = 1:NX
for j = 1:NZ
if i <= pml && j <= pml
x = pml - i;
z = pml - j;
ddx(i, j) = -log(R) * 3 * Vmax * x^2 / (2 * plx^2);
ddz(i, j) = -log(R) * 3 * Vmax * z^2 / (2 * plz^2);
elseif i <= pml && j > NZ - pml
x = pml - i;
z = j - (NZ - pml);
ddx(i, j) = -log(R) * 3 * Vmax * x^2 / (2 * plx^2);
ddz(i, j) = -log(R) * 3 * Vmax * z^2 / (2 * plz^2);
elseif i > NX - pml && j <= pml
x = i - (NX - pml);
z = pml - j;
ddx(i, j) = -log(R) * 3 * Vmax * x^2 / (2 * plx^2);
ddz(i, j) = -log(R) * 3 * Vmax * z^2 / (2 * plz^2);
elseif i > NX - pml && j > NZ - pml
x = i - (NX - pml);
z = j - (NZ - pml);
ddx(i, j) = -log(R) * 3 * Vmax * x^2 / (2 * plx^2);
ddz(i, j) = -log(R) * 3 * Vmax * z^2 / (2 * plz^2);
elseif i > pml && i <= NX - pml && j <= pml
z = pml - j;
ddx(i, j) = 0;
ddz(i, j) = -log(R) * 3 * Vmax * z^2 / (2 * plz^2);
elseif i > pml && i <= NX - pml && j > NZ - pml
z = j - (NZ - pml);
ddx(i, j) = 0;
ddz(i, j) = -log(R) * 3 * Vmax * z^2 / (2 * plz^2);
elseif i <= pml && j > pml && j <= NZ - pml
x = pml - i;
ddx(i, j) = -log(R) * 3 * Vmax * x^2 / (2 * plx^2);
ddz(i, j) = 0;
elseif i > NX - pml && j > pml && j <= NZ - pml
x = i - (NX - pml);
ddx(i, j) = -log(R) * 3 * Vmax * x^2 / (2 * plx^2);
ddz(i, j) = 0;
else
ddx(i, j) = 0;
ddz(i, j) = 0;
end
end
end
% Coefficients for finite difference
cof = zeros(1, N);
if N == 1
cof(1) = 1.0;
elseif N == 2
cof = [1.125, -0.041666667];
elseif N == 3
cof = [1.171875, -0.065104167, 0.0046875];
elseif N == 4
cof = [1.196289, -0.0797526, 0.009570313, -0.0006975447];
elseif N == 5
cof = [1.2112427, -0.08972168, 0.013842773, -0.0017656599, 0.00011867947];
elseif N == 6
cof = [1.2213364, -0.096931458, 0.017447662, -0.0029672895, 0.00035900540, -0.000021847812];
elseif N == 7
cof = [1.2286062, -0.10238385, 0.02047677, -0.0041789327, 0.00068945355, -0.000076922503, 0.0000042365148];
elseif N == 8
cof = [1.2340911, -0.10664985, 0.023036367, -0.0053423856, 0.0010772712, -0.00016641888, 0.000017021711, -0.00000085234642];
end
% Main time loop
for k = 1:NT
% Update stresses
for i = N+1:NX-N
for j = N+1:NZ-N
pxVx = 0; pzVx = 0; pxVz = 0; pzVz = 0;
for in = 0:N-1
pxVx = pxVx + cof(in+1) * (Vx(i+in+1,j) - Vx(i-in,j));
pxVz = pxVz + cof(in+1) * (Vz(i+in,j) - Vz(i-in-1,j));
pzVx = pzVx + cof(in+1) * (Vx(i,j+in+1) - Vx(i,j-in));
pzVz = pzVz + cof(in+1) * (Vz(i,j+in) - Vz(i,j-in-1));
end
Txx_x(i,j) = 1.0 / (1 + 0.5 * dt * ddx(i,j)) * ((1 - 0.5 * ddx(i,j) * dt) * Txx_x(i,j) + C_11(i,j) * dt / dx * pxVx + C_15(i,j) * dt / dx * pxVz);
Txx_z(i,j) = 1.0 / (1 + 0.5 * dt * ddz(i,j)) * ((1 - 0.5 * ddz(i,j) * dt) * Txx_z(i,j) + C_13(i,j) * dt / dz * pzVz + C_15(i,j) * dt / dz * pzVx);
Tzz_x(i,j) = 1.0 / (1 + 0.5 * dt * ddx(i,j)) * ((1 - 0.5 * ddx(i,j) * dt) * Tzz_x(i,j) + C_13(i,j) * dt / dx * pxVx + C_35(i,j) * dt / dx * pxVz);
Tzz_z(i,j) = 1.0 / (1 + 0.5 * dt * ddz(i,j)) * ((1 - 0.5 * ddz(i,j) * dt) * Tzz_z(i,j) + C_33(i,j) * dt / dz * pzVz + C_35(i,j) * dt / dz * pzVx);
Txx(i,j) = Txx_x(i,j) + Txx_z(i,j);
Tzz(i,j) = Tzz_x(i,j) + Tzz_z(i,j);
% Source term
if i == SX && j == SZ
tmp = (PI * f0 * (k * dt - t0))^2;
Txx_x(i,j) = Txx_x(i,j) + exp(-tmp) * (1 - 2 * tmp);
Txx_z(i,j) = Txx_z(i,j) + exp(-tmp) * (1 - 2 * tmp);
Tzz_x(i,j) = Txx_x(i,j);
Tzz_z(i,j) = Txx_z(i,j);
end
pxVx = 0; pzVx = 0; pxVz = 0; pzVz = 0;
for in = 0:N-1
pxVx = pxVx + cof(in+1) * (Vx(i+in+1,j) - Vx(i-in,j));
pxVz = pxVz + cof(in+1) * (Vz(i+in,j) - Vz(i-in-1,j));
pzVx = pzVx + cof(in+1) * (Vx(i,j+in+1) - Vx(i,j-in));
pzVz = pzVz + cof(in+1) * (Vz(i,j+in) - Vz(i,j-in-1));
end
Txz_x(i,j) = 1.0 / (1 + 0.5 * dt * ddx(i,j)) * ((1 - 0.5 * ddx(i,j) * dt) * Txz_x(i,j) + C_15(i,j) * dt / dx * pxVx + C_55(i,j) * dt / dx * pxVz);
Txz_z(i,j) = 1.0 / (1 + 0.5 * dt * ddz(i,j)) * ((1 - 0.5 * ddz(i,j) * dt) * Txz_z(i,j) + C_35(i,j) * dt / dz * pzVz + C_55(i,j) * dt / dz * pzVx);
Txz(i,j) = Txz_x(i,j) + Txz_z(i,j);
end
end
% Update velocities
for i = N+1:NX-N
for j = N+1:NZ-N
pxTxx = 0; pzTxz = 0;
for in = 0:N-1
pxTxx = pxTxx + cof(in+1) * (Txx(i+in,j) - Txx(i-in-1,j));
pzTxz = pzTxz + cof(in+1) * (Txz(i,j+in) - Txz(i,j-in-1));
end
Vx_x(i,j) = 1.0 / (1 + 0.5 * dt * ddx(i,j)) * ((1 - 0.5 * ddx(i,j) * dt) * Vx_x(i,j) + dt / Rou(i,j) / dx * pxTxx);
Vx_z(i,j) = 1.0 / (1 + 0.5 * dt * ddz(i,j)) * ((1 - 0.5 * ddz(i,j) * dt) * Vx_z(i,j) + dt / Rou(i,j) / dz * pzTxz);
Vx(i,j) = Vx_x(i,j) + Vx_z(i,j);
pxTxz = 0; pzTzz = 0;
for in = 0:N-1
pxTxz = pxTxz + cof(in+1) * (Txz(i+in+1,j) - Txz(i-in,j));
pzTzz = pzTzz + cof(in+1) * (Tzz(i,j+in+1) - Tzz(i,j-in));
end
Vz_x(i,j) = 1.0 / (1 + 0.5 * dt * ddx(i,j)) * ((1 - 0.5 * ddx(i,j) * dt) * Vz_x(i,j) + dt / Rou(i,j) / dx * pxTxz);
Vz_z(i,j) = 1.0 / (1 + 0.5 * dt * ddz(i,j)) * ((1 - 0.5 * ddz(i,j) * dt) * Vz_z(i,j) + dt / Rou(i,j) / dz * pzTzz);
Vz(i,j) = Vz_x(i,j) + Vz_z(i,j);
end
end
% Plot the wavefield for animation
ndt = 10;
if k>=200 & mod(k, ndt) == 0
imagesc(Txx+Tzz);
colormap('jet');
colorbar;
% caxis([-1, 1]);
title(['Wavefield at time step: ', num2str(k)]);
xlabel('X');
ylabel('Z');
drawnow;
frame = getframe(gcf);
im = frame2im(frame);
[imind, cm] = rgb2ind(im, 256);
if k == 200
imwrite(imind, cm, 'Wavefield.gif', 'gif', 'Loopcount', inf, 'DelayTime', 0.1);
else
imwrite(imind, cm, 'Wavefield.gif', 'gif', 'WriteMode', 'append', 'DelayTime', 0.1);
end
end
% Record data
for i = 1:NX
rz = SZ;
data_vx(i,k) = Vx(i,rz);
data_vz(i,k) = Vz(i,rz);
end
% % Save data every 1000 time steps
% if mod(k, 1000) == 0
% Vx_filename = sprintf('Vx_%d.dat', k);
% Vz_filename = sprintf('Vz_%d.dat', k);
% save(Vx_filename, 'Vx', '-ascii');
% save(Vz_filename, 'Vz', '-ascii');
% end
end
% % Save final data
% save('Txx.dat', 'Txx', '-ascii');
% save('Tzz.dat', 'Tzz', '-ascii');
% T = 0.5 * (Txx + Tzz);
% save('T.dat', 'T', '-ascii');
% save('Txz.dat', 'Txz', '-ascii');
% save('Vx.dat', 'Vx', '-ascii');
% save('Vz.dat', 'Vz', '-ascii');
% save('data_vx.dat', 'data_vx', '-ascii');
% save('data_vz.dat', 'data_vz', '-ascii');
% save('Vp.dat', 'Vp', '-ascii');
% % Plot the wavefield
% imagesc(Vx);
% colormap('jet');
% colorbar;
% title('Vx Wavefield');
% xlabel('X');
% ylabel('Z');
四. 数值算例
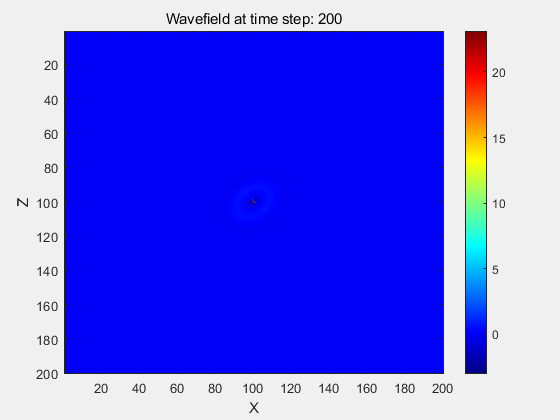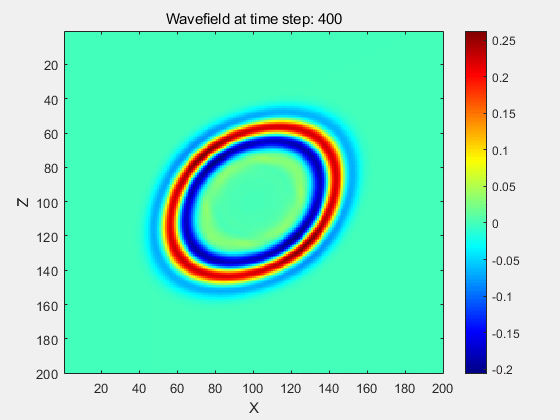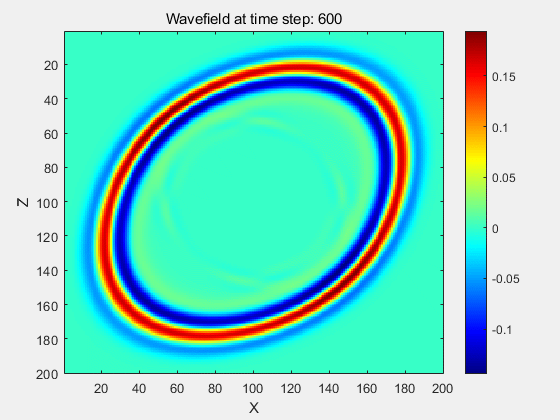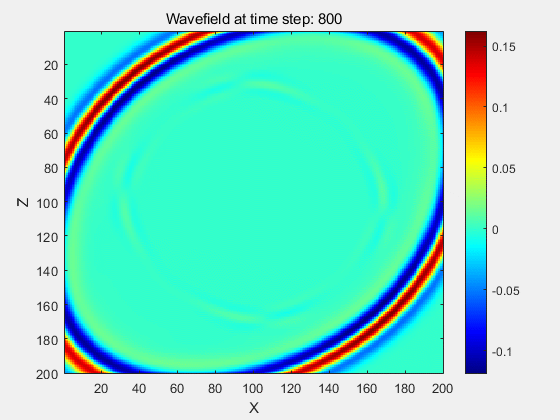
例1:均匀ISO,VTI,TTI介质波场模拟
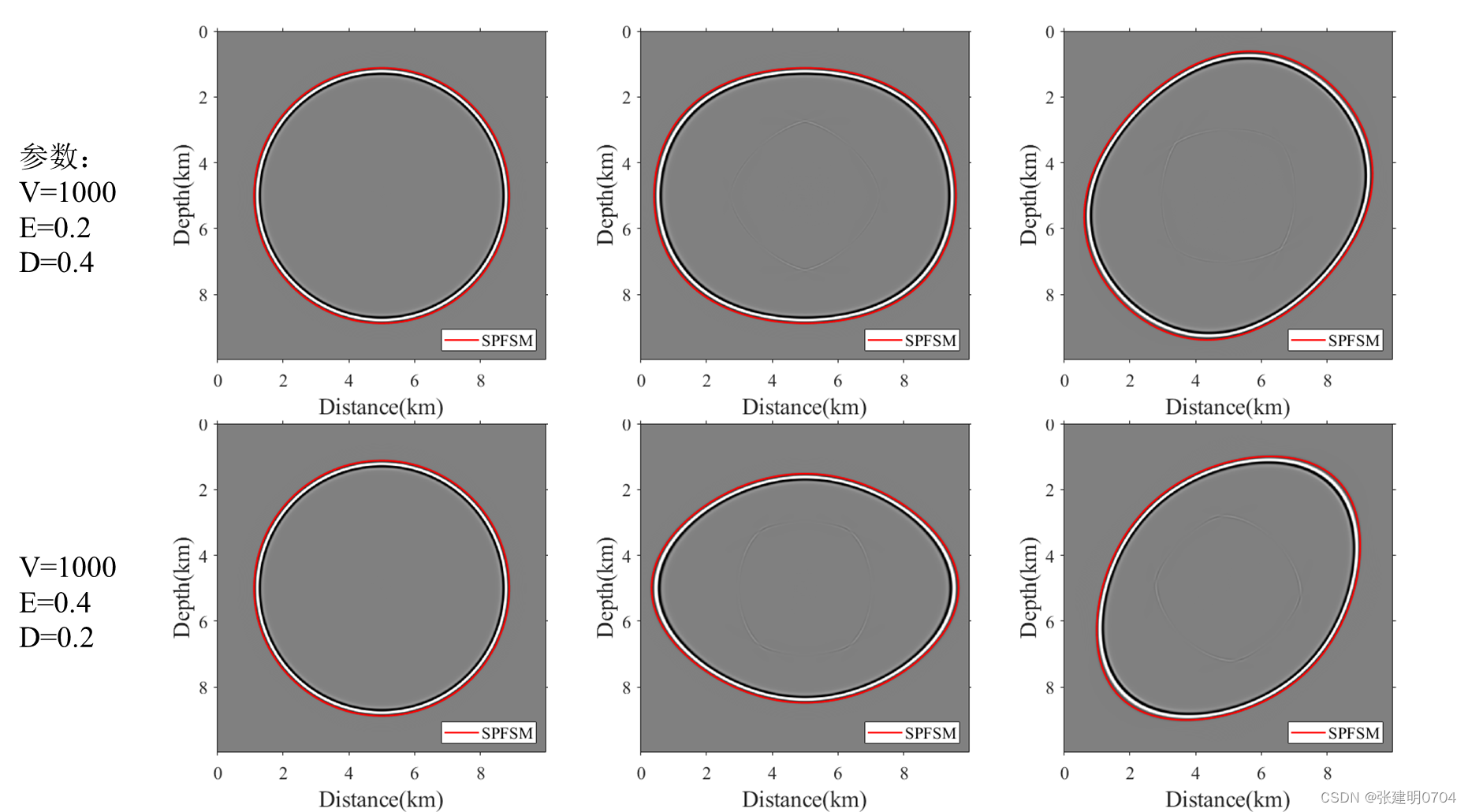
MATLAB代码模拟结果:
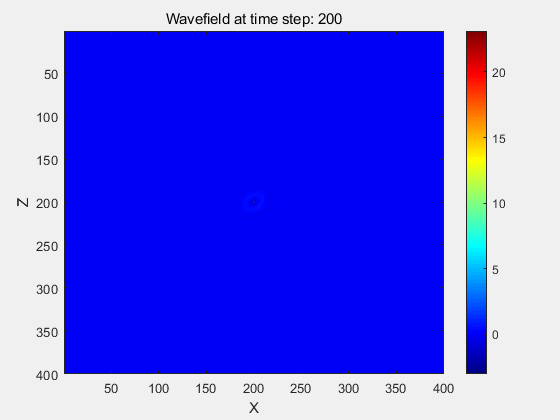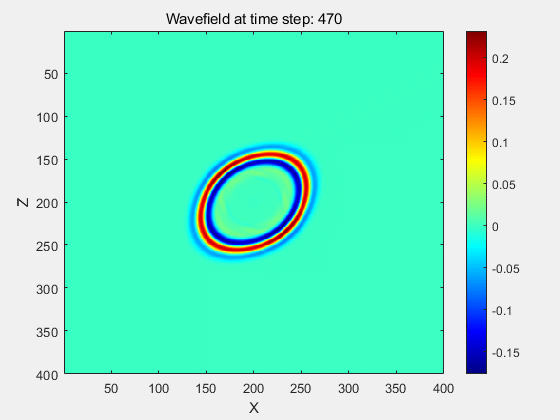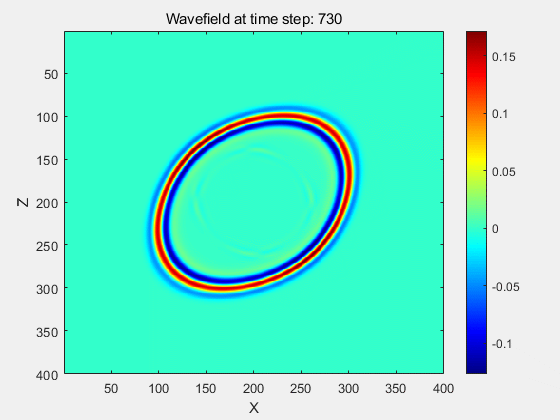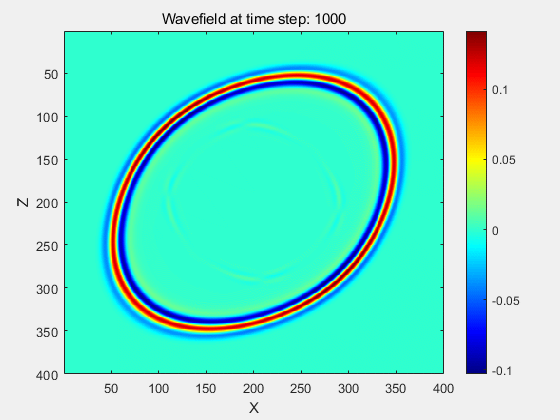
其余的例子均是用C++代码运行的结果。
例2:各向同性起伏界面声波波场模拟
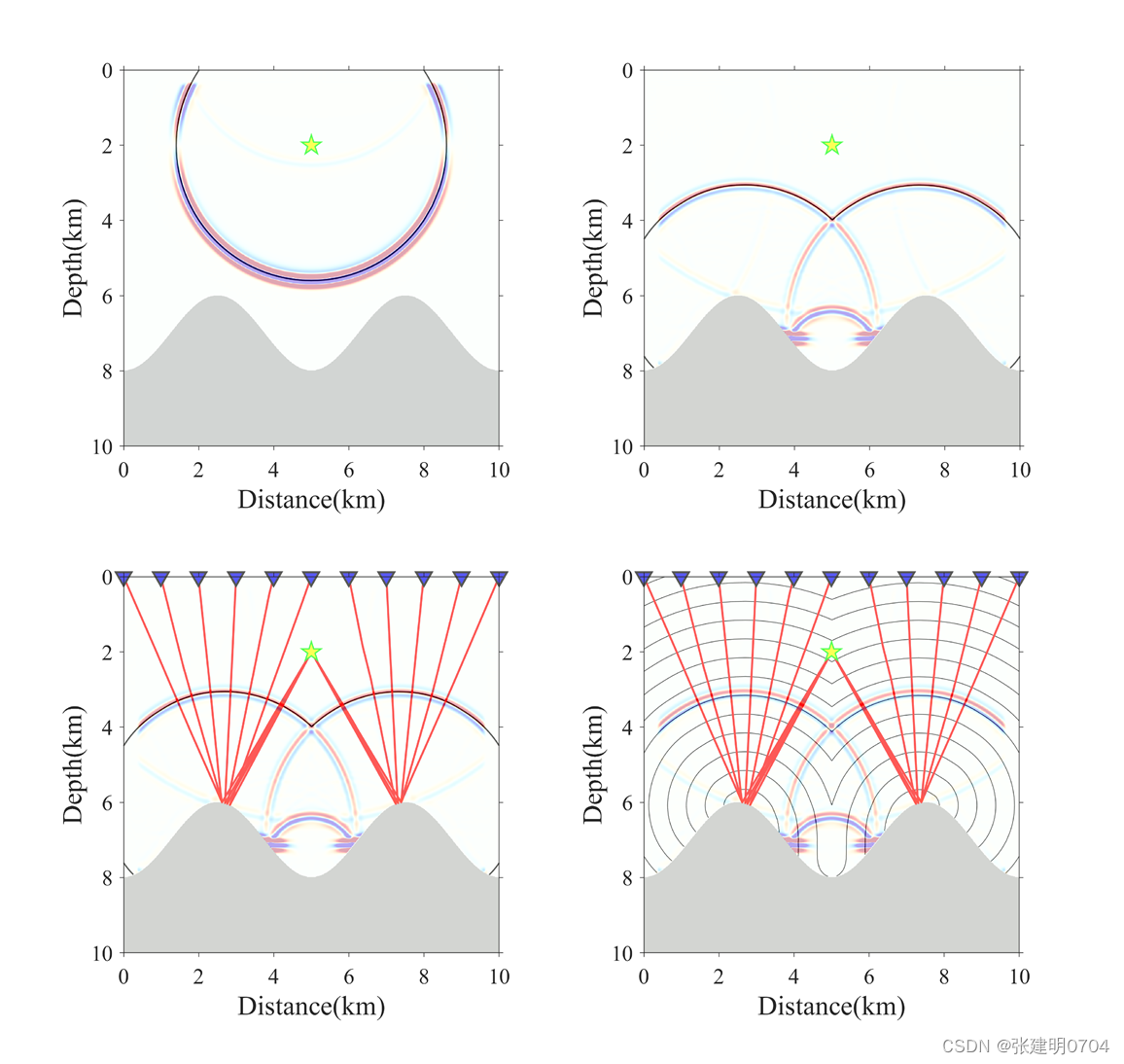
例3:水平和起伏界面各向同性弹性波场模拟
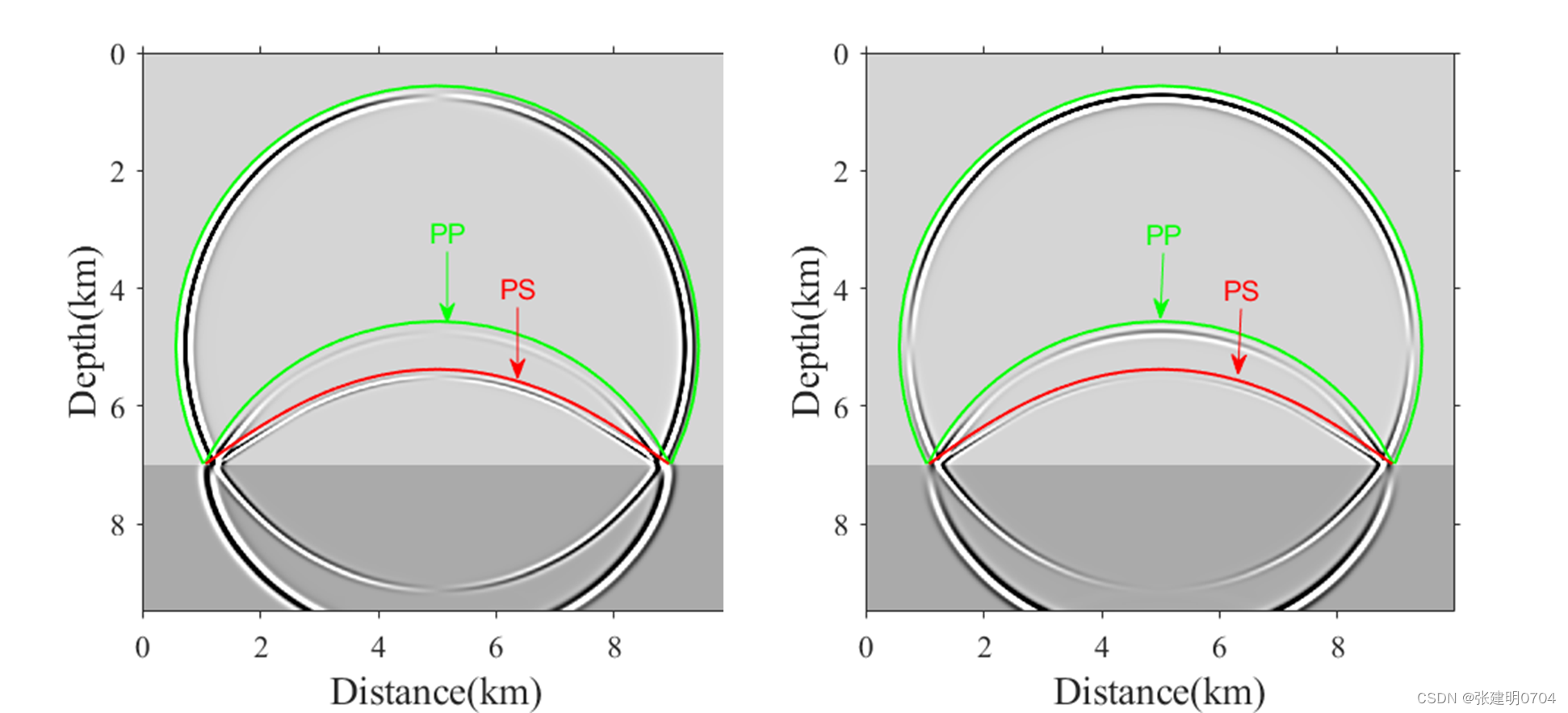
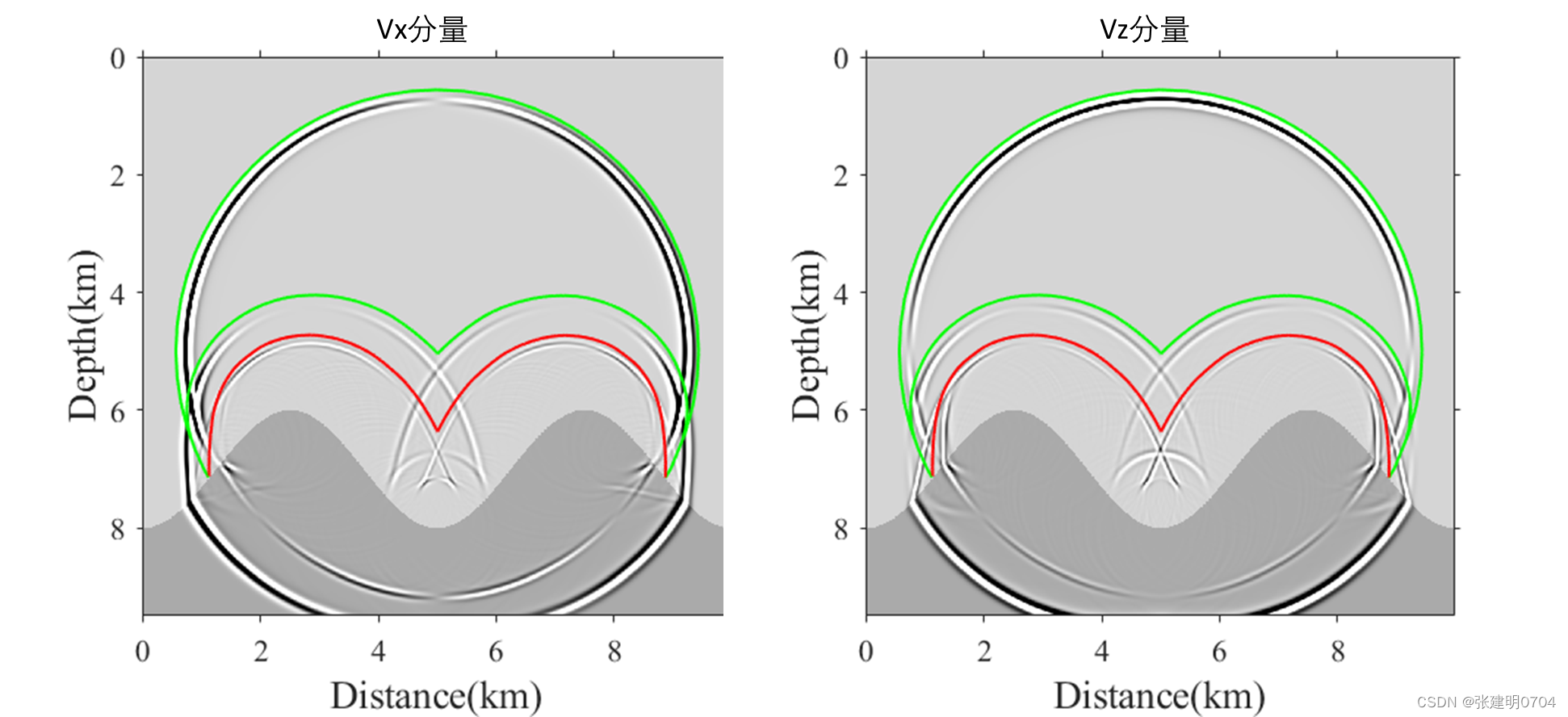
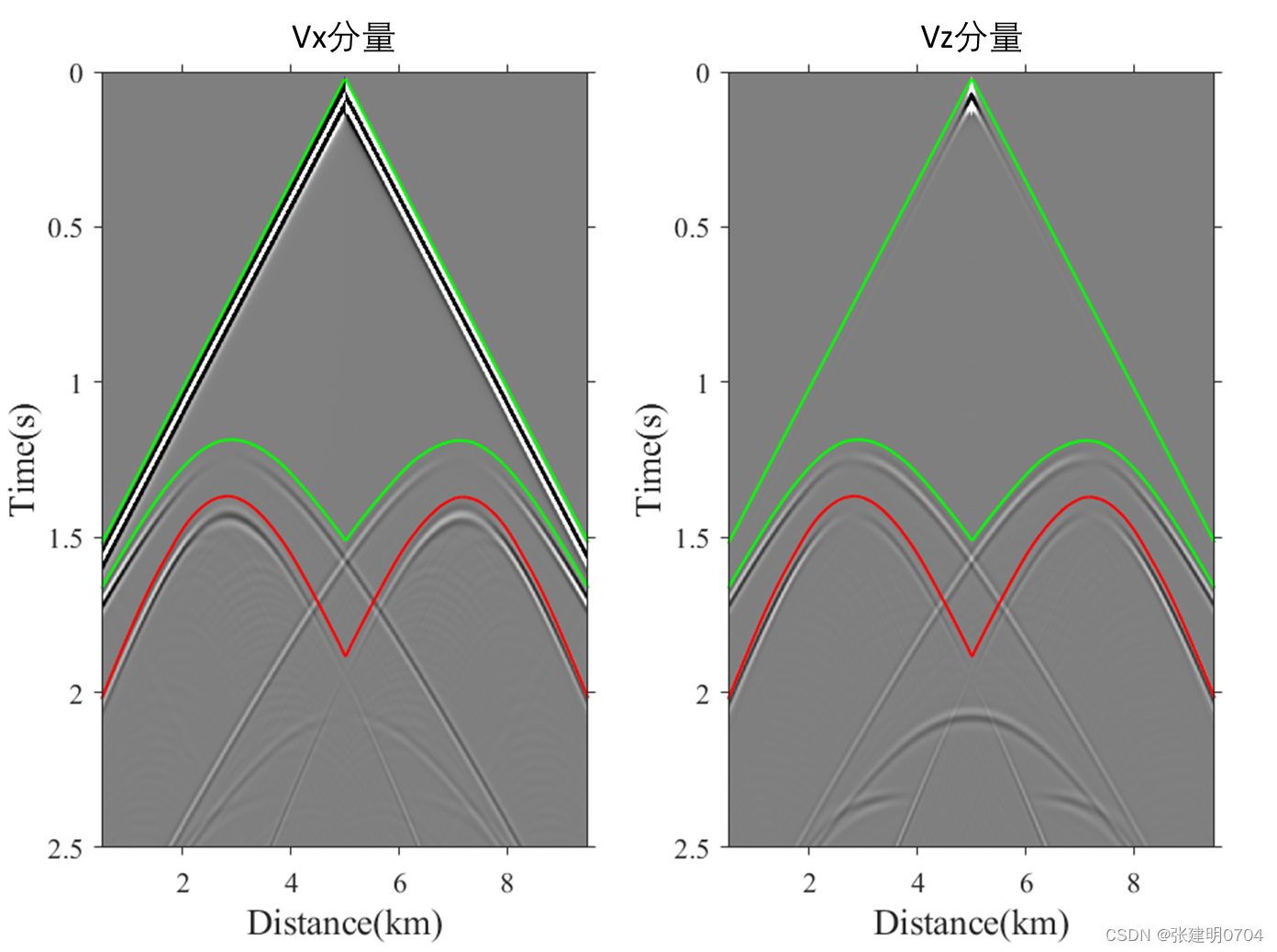
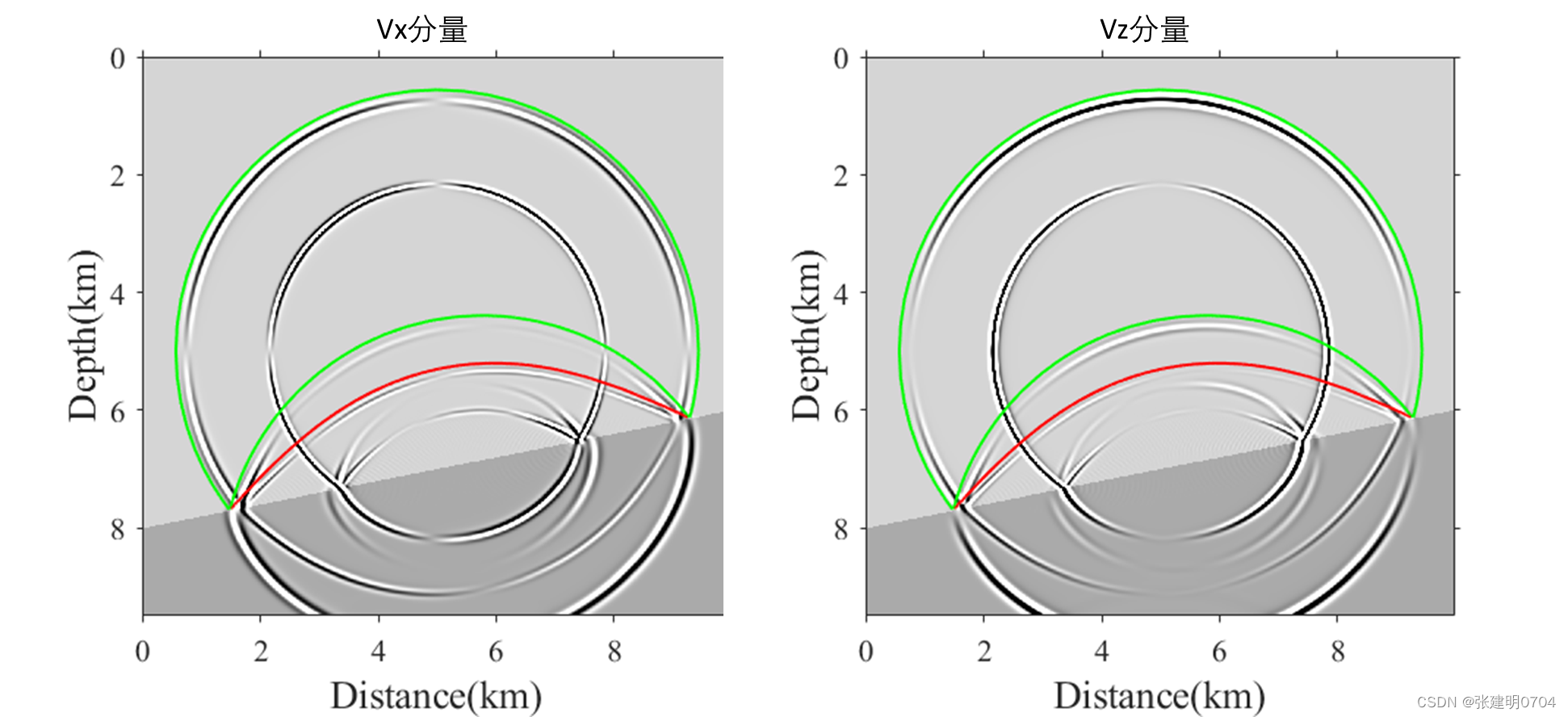
例4:各向同性Marmousi模型波场模拟
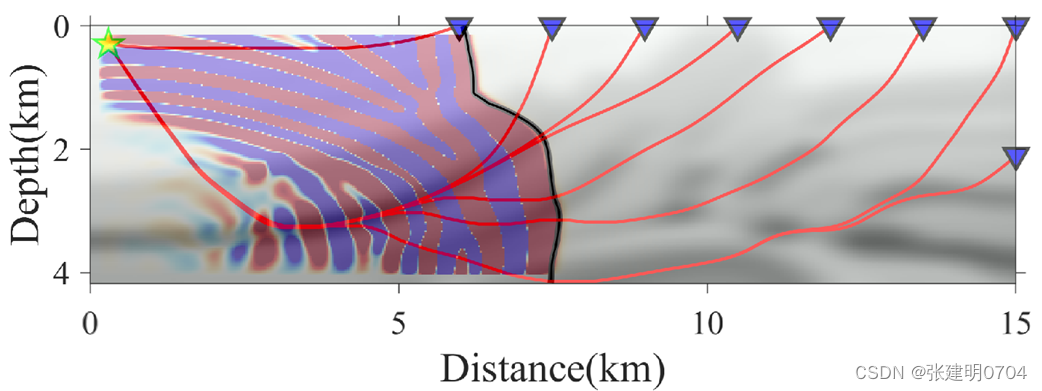
例5:起伏多层介质弹性波场模拟
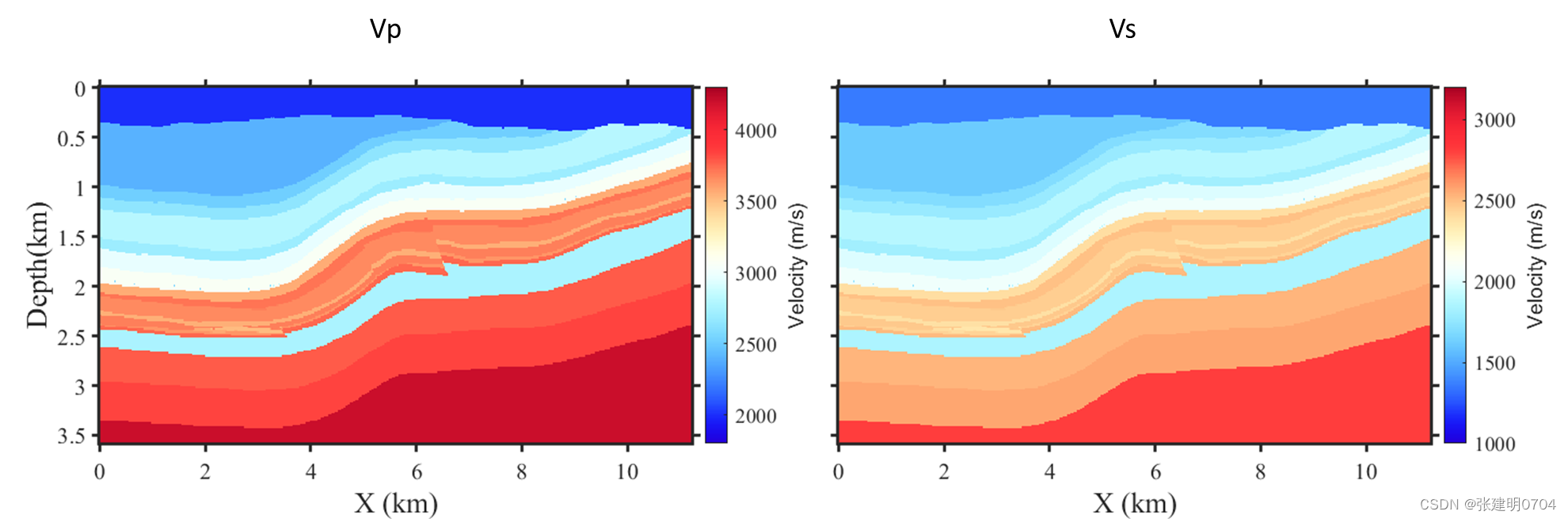
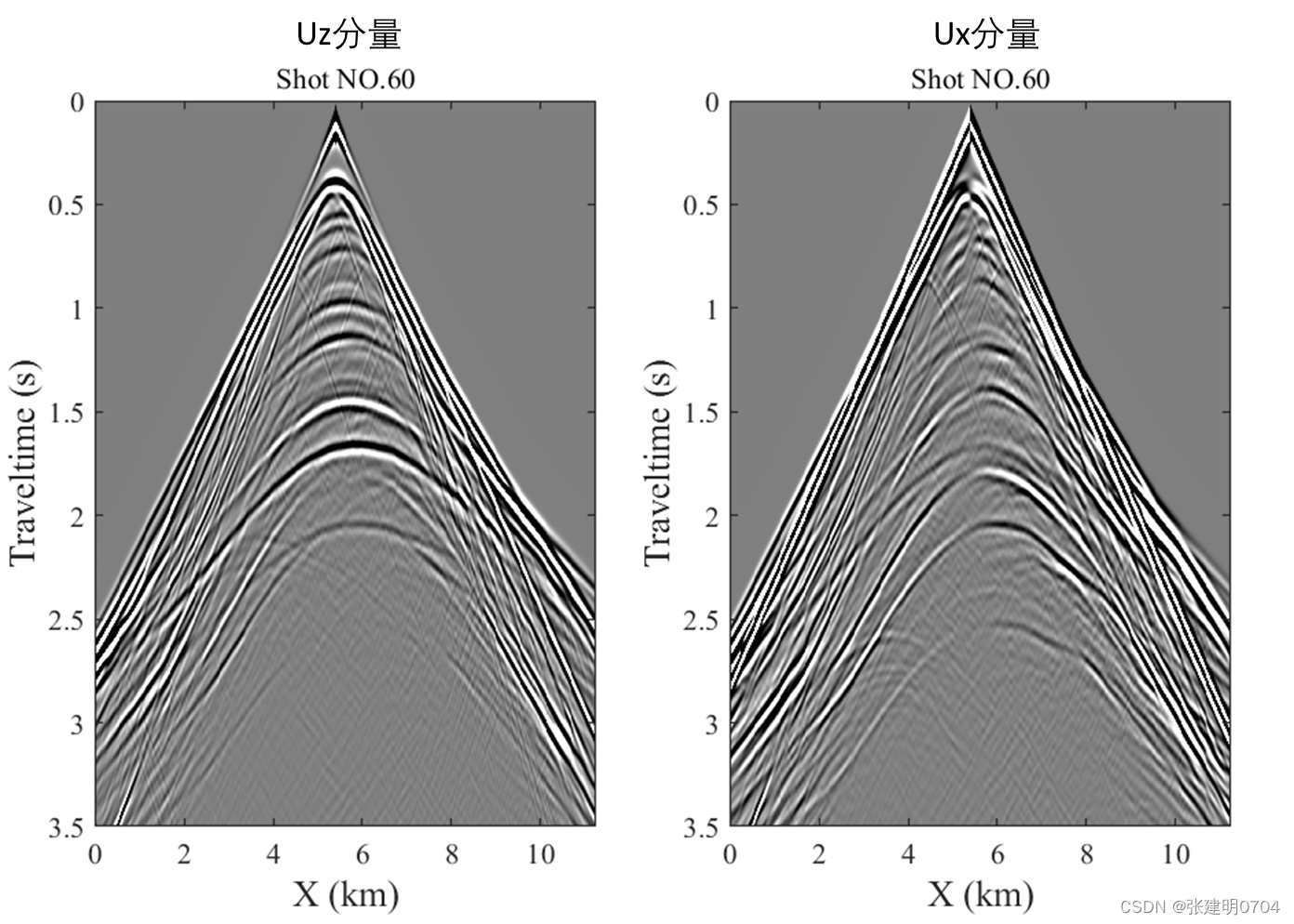
例6:VTI(BP 2007模型)介质拟声波场模拟
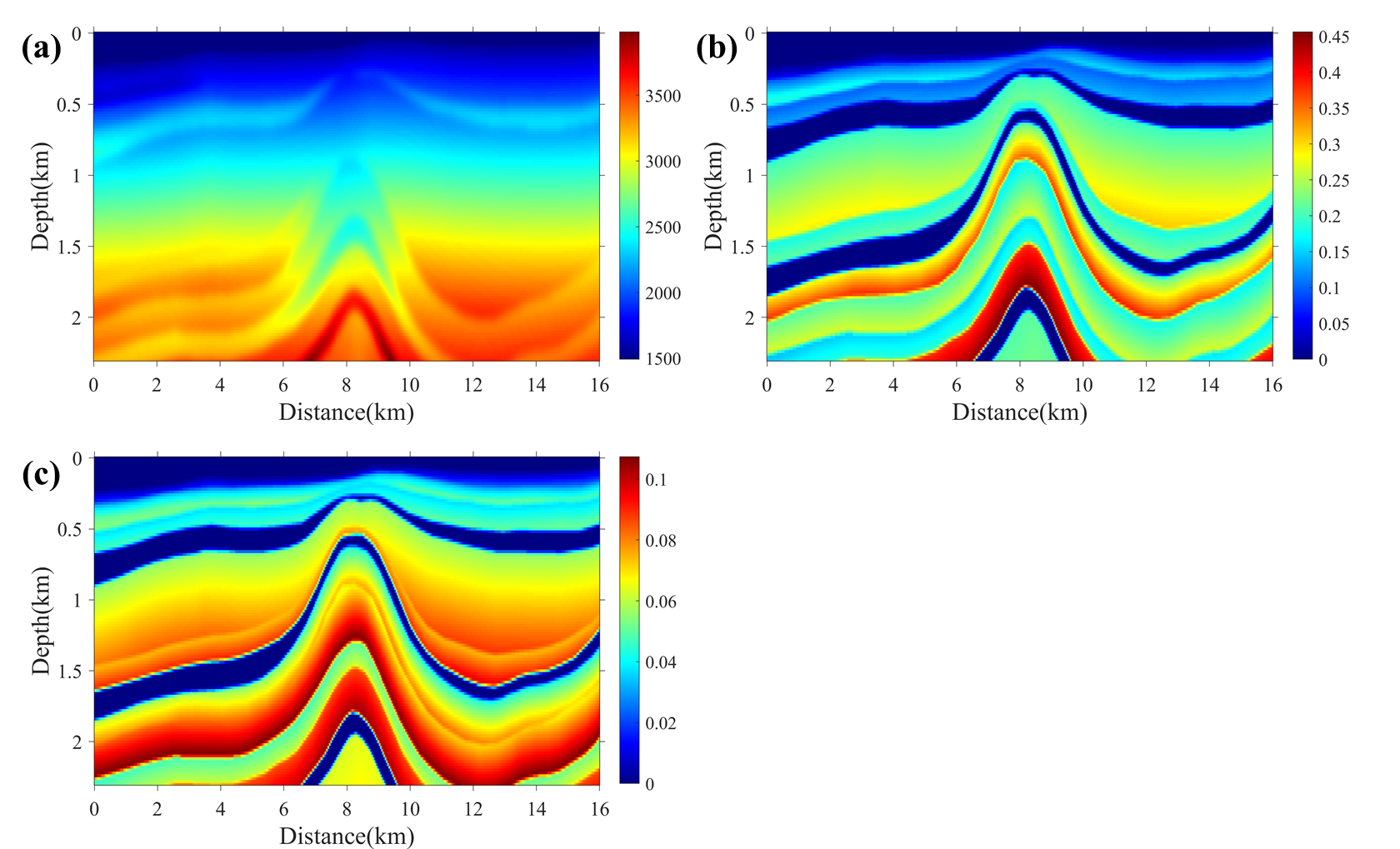
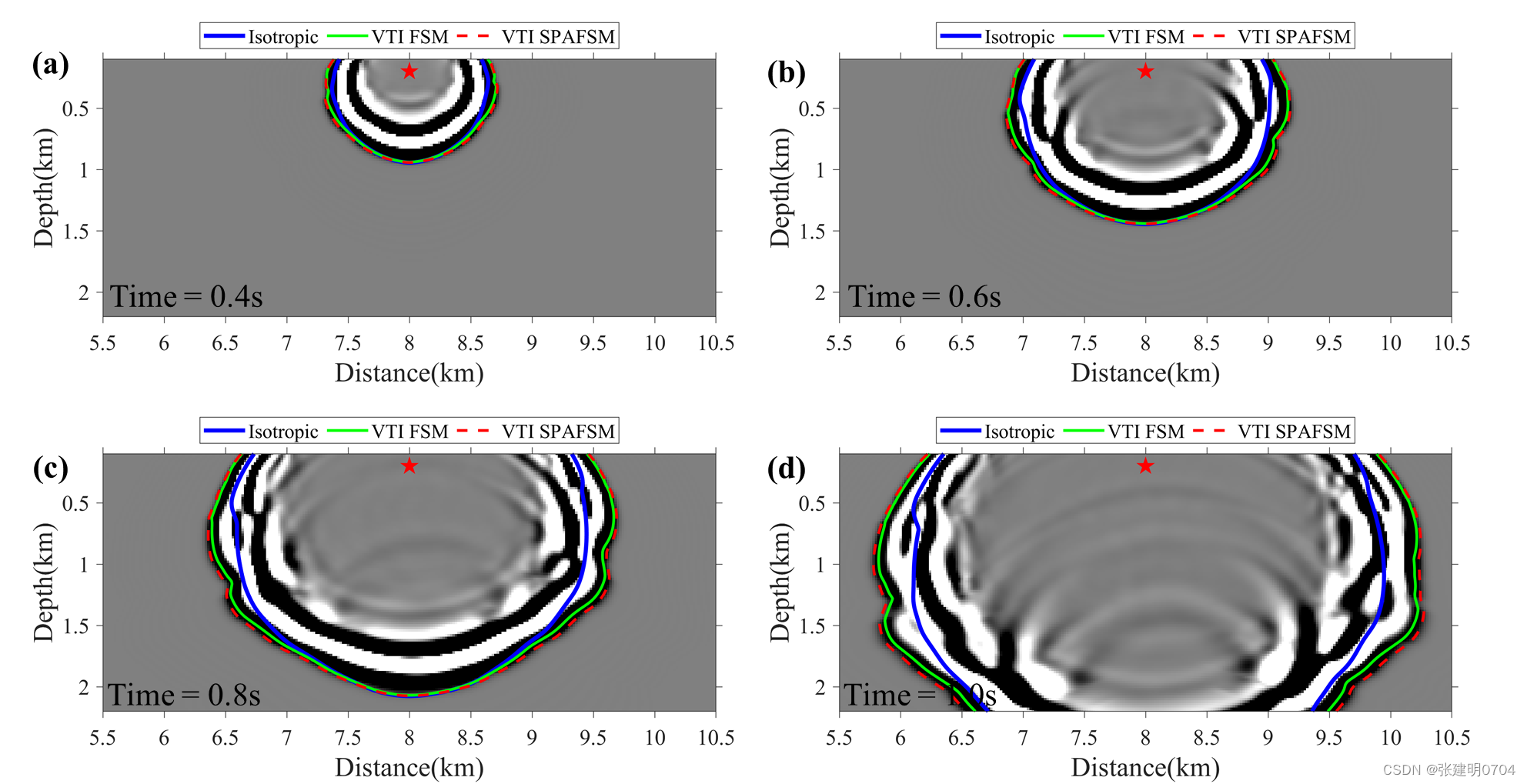
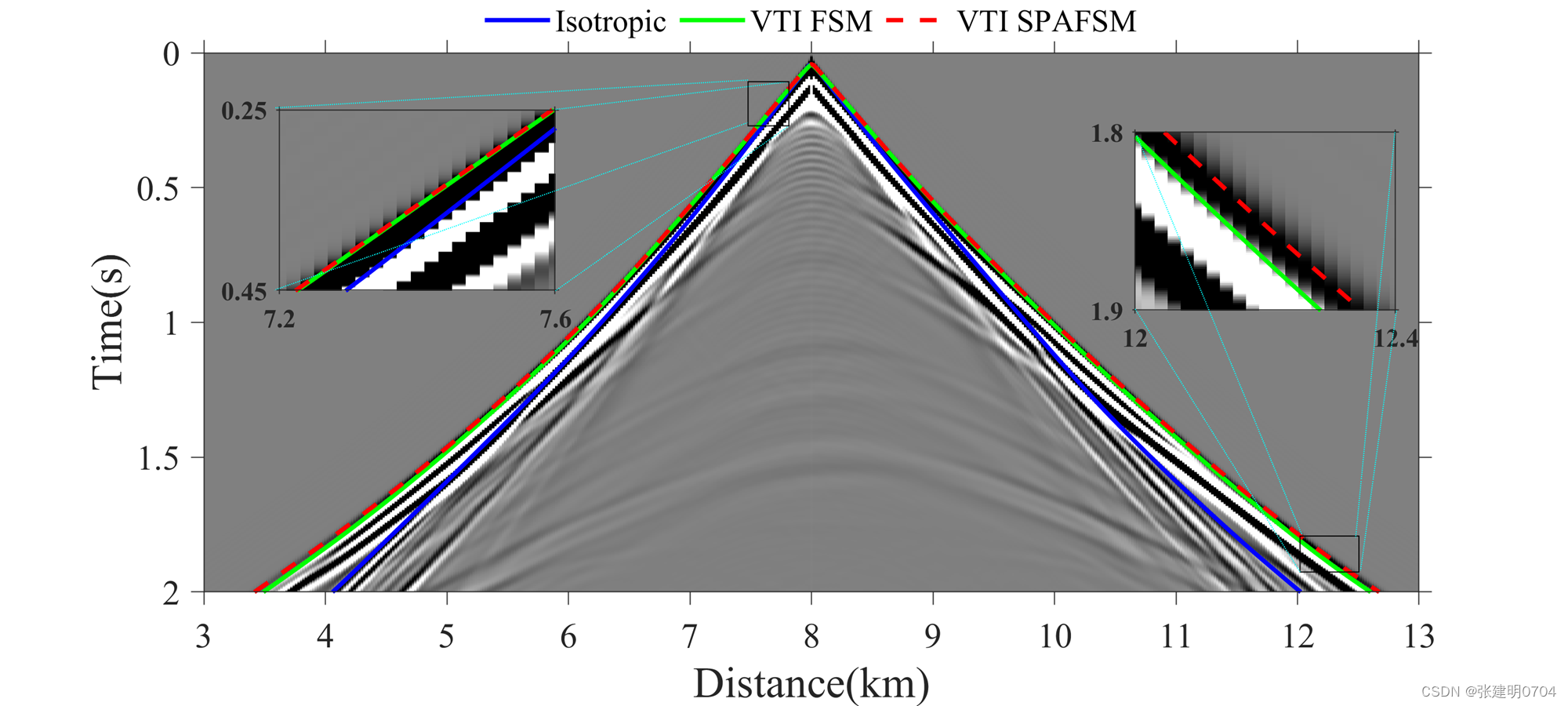
五. 补充代码(PML外置)
下面是PML外置的程序,没啥技术含量,参考一下就好。
5.1 C++代码
/********************************************************************************/
/***********Elastic Velocity-Stress Finite-difference Modeling with PML**********/
/**************High Order (Highest: sixteen order) Finite-difference*************/
/***************************Written By Zhang Jianming,2022.10.10*****************/
/***************************************CopyRight********************************/
#include<stdio.h>
#include<math.h>
#include<iostream>
#include<fstream>
#include<iomanip>
using namespace std;
#define PI 3.1415926
#define dx 10
#define dz 10
#define pml 50
#define NX (1000+2*pml)
#define NZ (1000+2*pml)
#define NT 10001
#define dt 0.005
#define N 6
float fi=0*(PI/4.0);
int main()
{
//cout<<"sin(pi/6)="<<sin(PI/6)<<endl;
float **Txx=new float*[NX],**Txx_x=new float*[NX],**Txx_z=new float*[NX];
float **Tzz=new float*[NX],**Tzz_x=new float*[NX],**Tzz_z=new float*[NX];
float **Txz=new float*[NX],**Txz_x=new float*[NX],**Txz_z=new float*[NX];
float **Vx=new float*[NX],**Vx_x=new float*[NX],**Vx_z=new float*[NX];
//A wierd question: icpc compeler broke down using the below Vz, why?
float **Vz=new float*[NX],**Vz_x=new float*[NX],**Vz_z=new float*[NX];
float **L=new float*[NX],**M=new float*[NX],**e=new float*[NX];
float **C11=new float*[NX],**C33=new float*[NX],**C44=new float*[NX],**C66=new float*[NX],**C13=new float*[NX],**Rou=new float*[NX];
float **C_11=new float*[NX],**C_13=new float*[NX],**C_15=new float*[NX],**C_33=new float*[NX],**C_35=new float*[NX],**C_55=new float*[NX],**O=new float*[NX];
float **Vp=new float*[NX],**Eps=new float*[NX],**Del=new float*[NX],**Vs=new float*[NX],**Gam=new float*[NX],**F=new float*[NX];
float **data_vx=new float*[NX],**data_vz=new float*[NX];//Observed Vx and Vz components
for(int i=0;i<NX;i++)
{
Txx[i]=new float[NZ];Txx_x[i]=new float[NZ];Txx_z[i]=new float[NZ];
Tzz[i]=new float[NZ];Tzz_x[i]=new float[NZ];Tzz_z[i]=new float[NZ];
Txz[i]=new float[NZ];Txz_x[i]=new float[NZ];Txz_z[i]=new float[NZ];
Vx[i]=new float[NZ];Vx_x[i]=new float[NZ];Vx_z[i]=new float[NZ];
Vz[i]=new float[NZ];Vz_x[i]=new float[NZ];Vz_z[i]=new float[NZ];
L[i]=new float[NZ];M[i]=new float[NZ];e[i]=new float[NZ];
C11[i]=new float[NZ];C33[i]=new float[NZ];C44[i]=new float[NZ];C66[i]=new float[NZ];C13[i]=new float[NZ];Rou[i]=new float[NZ];
Vp[i]=new float[NZ];Eps[i]=new float[NZ];Del[i]=new float[NZ];Vs[i]=new float[NZ];Gam[i]=new float[NZ];F[i]=new float[NZ];
C_11[i]=new float[NZ];C_13[i]=new float[NZ];C_15[i]=new float[NZ];C_33[i]=new float[NZ];C_35[i]=new float[NZ];C_55[i]=new float[NZ];O[i]=new float[NZ];
for(int j=0;j<NZ;j++)
{
Txx[i][j]=0;Txx_x[i][j]=0;Txx_z[i][j]=0;
Tzz[i][j]=0;Tzz_x[i][j]=0;Tzz_z[i][j]=0;
Txz[i][j]=0;Txz_x[i][j]=0;Txz_z[i][j]=0;
Vx[i][j]=0;Vx_x[i][j]=0;Vx_z[i][j]=0;
Vz[i][j]=0;Vz_x[i][j]=0;Vz_z[i][j]=0;
}
data_vx[i]=new float[NT];data_vz[i]=new float[NT];
for(int j=0;j<NT;j++)
{
data_vx[i][j]=0;
data_vz[i][j]=0;
}
}
//FILE *filename;
//filename=fopen("vp.dat","rb");
////for(int i=0;i<NX;i++)
//// for(int j=0;j<NZ;j++)
//for (int i = pml; i < NX-pml; i++)
// for (int j = pml; j < NZ-pml; j++)
// fread(&Vp[i][j], sizeof(float), 1, filename);
//fclose(filename);
//FILE *filenameE;
//filenameE=fopen("eps.dat","rb");
////for(int i=0;i<NX;i++)
//// for(int j=0;j<NZ;j++)
//for (int i = pml; i < NX-pml; i++)
// for (int j = pml; j < NZ-pml; j++)
// fread(&Eps[i][j], sizeof(float), 1, filenameE);
//fclose(filenameE);
//FILE *filenameD;
//filenameD=fopen("delta.dat","rb");
////for(int i=0;i<NX;i++)
//// for(int j=0;j<NZ;j++)
//for (int i = pml; i < NX-pml; i++)
// for (int j = pml; j < NZ-pml; j++)
// fread(&Del[i][j], sizeof(float), 1, filenameD);
//fclose(filenameD);
////Model extroplate
//for(int i=0;i<pml;i++)
// for(int j=0;j<NZ;j++)
// {
// Vp[i][j]=Vp[pml][j];
// Eps[i][j]=Eps[pml][j];
// Del[i][j]=Del[pml][j];
// }
//for(int i=NX-pml;i<NX;i++)
// for(int j=0;j<NZ;j++)
// {
// Vp[i][j]=Vp[NX-pml-1][j];
// Eps[i][j]=Eps[NX-pml-1][j];
// Del[i][j]=Del[NX-pml-1][j];
// }
//for(int i=0;i<NX;i++)
// for(int j=0;j<pml;j++)
// {
// Vp[i][j]=Vp[i][pml];
// Eps[i][j]=Eps[i][pml];
// Del[i][j]=Del[i][pml];
// }
//for(int i=0;i<NX;i++)
// for(int j=NZ-pml;j<NZ;j++)
// {
// Vp[i][j]=Vp[i][NZ-pml-1];
// Eps[i][j]=Eps[i][NZ-pml-1];
// Del[i][j]=Del[i][NZ-pml-1];
// }
int i,j,k,f0=15;float t0=1.2/f0;
//int SX=NX/2;int SZ=pml+10;
int SX=NX/2;int SZ=NZ/2;
//int SX=2*pml;int SZ=2*pml;
FILE *fp1,*fp11,*fp12,*fp2,*fp3,*fp4,*fp5,*fp6,*fp7;
float ddx[NX][NZ];float ddz[NX][NZ];
float R=0.001,Vmax=7500;
int x,z,plx,plz;
for(i=0;i<NX;i++)
for(j=0;j<NZ;j++)
{
//Iso
//L[i][j]=1.19*pow(10, 10);M[i][j]=5.4*pow(10, 9);e[i][j]=2.0*pow(10, 3);
//C11[i][j]=L[i][j]+2*M[i][j];
//C33[i][j]=C11[i][j];
//C44[i][j]=M[i][j];
//C66[i][j]=M[i][j];
//C13[i][j]=L[i][j];
//Rou[i][j]=e[i][j];
//Ice
//C11[i][j]=13.33*pow(10, 9);
//C33[i][j]=14.28*pow(10, 9);
//C44[i][j]=3.26*pow(10, 9);
//C66[i][j]=3.65*pow(10, 9);
//C13[i][j]=5.08*pow(10, 9);
//Rou[i][j]=0.91*pow(10, 3);
//Quartz
//C11[i][j]=116.6*pow(10, 9);
//C33[i][j]=110.40*pow(10, 9);
//C44[i][j]=36.06*pow(10, 9);
//C66[i][j]=49.95*pow(10, 9);
//C13[i][j]=32.8*pow(10, 9);
//Rou[i][j]=2.65*pow(10, 3);
//Mantle
//C11[i][j]=212.8*pow(10, 9);
//C33[i][j]=249.18*pow(10, 9);
//C44[i][j]=70.47*pow(10, 9);
//C66[i][j]=66.72*pow(10, 9);
//C13[i][j]=76.24*pow(10, 9);
//Rou[i][j]=3.22*pow(10, 3);
//Ref
//C11[i][j]=25.5*pow(10, 9);
//C33[i][j]=18.4*pow(10, 9);
//C44[i][j]=5.6*pow(10, 9);
//C66[i][j]=5.6*pow(10, 9);
//C13[i][j]=10.4*pow(10, 9);
//Rou[i][j]=2.44*pow(10, 3);
//Thomsen
Vp[i][j]=3000;
Eps[i][j]*=0;
Del[i][j]=0.0;
Vs[i][j]=2000;//Vp[i][j]/sqrt(3);
Gam[i][j]=0.1;
if(j>7.0/10.0*NZ)
//if(j>-200*i/1000.0+800)
//if(j>-100*cos(2*PI*i/500.0)+700)
{
//Vp[i][j]=4000;
Vs[i][j]=2800;
//Vs[i][j]=2800;
}
if(j>8.0/10.0*NZ)
{
Vp[i][j]=4000;
//Vs[i][j]=2800;
}
//if(j>80) {Vp[i][j]=1000;Vs[i][j]=800;}
Rou[i][j]=3.44*pow(10, 3);
C11[i][j]=Rou[i][j]*(1.0+2*Eps[i][j])*pow(Vp[i][j],2);
C33[i][j]=Rou[i][j]*pow(Vp[i][j],2);
C44[i][j]=Rou[i][j]*pow(Vs[i][j],2);
C66[i][j]=Rou[i][j]*(1.0+2*Gam[i][j])*pow(Vs[i][j],2);
F[i][j]=1.0-pow(Vs[i][j],2)/pow(Vp[i][j],2);
C13[i][j]=Rou[i][j]*pow(Vp[i][j],2)*sqrt(F[i][j]*(F[i][j]+2*Del[i][j]))-Rou[i][j]*pow(Vs[i][j],2);
O[i][j]=fi;
C_11[i][j]=C11[i][j]*pow(cos(O[i][j]),4)+C33[i][j]*pow(sin(O[i][j]),4)+(2*C13[i][j]+4*C44[i][j])*pow(sin(O[i][j]),2)*pow(cos(O[i][j]),2);
C_13[i][j]=(C11[i][j]+C33[i][j]-4*C44[i][j])*pow(sin(O[i][j]),2)*pow(cos(O[i][j]),2)+C13[i][j]*(pow(sin(O[i][j]),4)+pow(cos(O[i][j]),4));
C_15[i][j]=(C13[i][j]-C11[i][j]+2*C44[i][j])*pow(sin(O[i][j]),1)*pow(cos(O[i][j]),3)-(C13[i][j]-C33[i][j]+2*C44[i][j])*pow(sin(O[i][j]),3)*pow(cos(O[i][j]),1);
C_33[i][j]=C11[i][j]*pow(sin(O[i][j]),4)+C33[i][j]*pow(cos(O[i][j]),4)+(2*C13[i][j]+4*C44[i][j])*pow(sin(O[i][j]),2)*pow(cos(O[i][j]),2);
C_35[i][j]=(C13[i][j]-C11[i][j]+2*C44[i][j])*pow(sin(O[i][j]),3)*pow(cos(O[i][j]),1)-(C13[i][j]-C33[i][j]+2*C44[i][j])*pow(sin(O[i][j]),1)*pow(cos(O[i][j]),3);
C_55[i][j]=(C11[i][j]+C33[i][j]-2*C13[i][j])*pow(sin(O[i][j]),2)*pow(cos(O[i][j]),2)+C44[i][j]*pow(pow(cos(O[i][j]),2)-pow(sin(O[i][j]),2),2);
}
//PML
plx=pml*dx;plz=pml*dz;
for(i=0;i<NX;i++)
for(j=0;j<NZ;j++)
{
if(i>=0&&i<pml&&j>=0&&j<pml)
{
x=pml-i;z=pml-j;
ddx[i][j]=-log(R)*3*Vmax*x*x/(2*plx*plx);
ddz[i][j]=-log(R)*3*Vmax*z*z/(2*plz*plz);
}
else if(i>=0&&i<pml&&j>NZ-pml&&j<NZ)
{
x=pml-i;z=j-(NZ-pml);
ddx[i][j]=-log(R)*3*Vmax*x*x/(2*plx*plx);
ddz[i][j]=-log(R)*3*Vmax*z*z/(2*plz*plz);
}
else if(i>NX-pml&&i<NX&&j>=0&&j<pml)
{
x=i-(NX-pml);z=pml-j;
ddx[i][j]=-log(R)*3*Vmax*x*x/(2*plx*plx);
ddz[i][j]=-log(R)*3*Vmax*z*z/(2*plz*plz);
}
else if(i>NX-pml&&i<NX&&j>NZ-pml&&j<NZ)
{
x=i-(NX-pml);z=j-(NZ-pml);
ddx[i][j]=-log(R)*3*Vmax*x*x/(2*plx*plx);
ddz[i][j]=-log(R)*3*Vmax*z*z/(2*plz*plz);
}
else if(i>=pml&&i<=NX-pml&&j>=0&&j<pml)
{
x=i-pml;z=pml-j;
ddx[i][j]=0;
ddz[i][j]=-log(R)*3*Vmax*z*z/(2*plz*plz);
}
else if(i>=pml&&i<=NX-pml&&j>NZ-pml&&j<NZ)
{
x=i-pml;z=j-(NZ-pml);
ddx[i][j]=0;
ddz[i][j]=-log(R)*3*Vmax*z*z/(2*plz*plz);
}
else if(i>=0&&i<pml&&j>=pml&&j<=NZ-pml)
{
x=pml-i;z=j-pml;
ddx[i][j]=-log(R)*3*Vmax*x*x/(2*plx*plx);
ddz[i][j]=0;
}
else if(i>NX-pml&&i<NX&&j>=pml&&j<=NZ-pml)
{
x=i-(NX-pml);z=j-pml;
ddx[i][j]=-log(R)*3*Vmax*x*x/(2*plx*plx);
ddz[i][j]=0;
}
else if(i>=pml&&i<=NX-pml&&j>=pml&&j<=NZ-pml)
{
x=i-pml;z=j-pml;
ddx[i][j]=0;
ddz[i][j]=0;
}
}
float cof[N];
if(N==1)
{ cof[0]=1.0;}
if(N==2)
{ cof[0]=1.125;cof[1]=-0.041666667;}
if(N==3)
{ cof[0]=1.171875;cof[1]=-0.065104167;cof[2]=0.0046875;}
if(N==4)
{ cof[0]=1.196289;cof[1]=-0.0797526;cof[2]=0.009570313;cof[3]=-0.0006975447;}
if(N==5)
{ cof[0]=1.2112427;cof[1]=-0.08972168;cof[2]=0.013842773;cof[3]=-0.0017656599;cof[4]=0.00011867947;}
if(N==6)
{ cof[0]=1.2213364;cof[1]=-0.096931458;cof[2]=0.017447662;cof[3]=-0.0029672895;cof[4]=0.00035900540;cof[5]=-0.000021847812;}
if(N==7)
{ cof[0]=1.2286062;cof[1]=-0.10238385;cof[2]=0.02047677;cof[3]=-0.0041789327;cof[4]=0.00068945355;cof[5]=-0.000076922503;cof[6]=0.0000042365148;}
if(N==8)
{ cof[0]=1.2340911;cof[1]=-0.10664985;cof[2]=0.023036367;cof[3]=-0.0053423856;cof[4]=0.0010772712;cof[5]=-0.00016641888;cof[6]=0.000017021711;cof[7]=-0.00000085234642;}
for(k=0;k<NT;k++)
{
for(i=N;i<NX-N;i++)
{
for(j=N;j<NZ-N;j++)
{
//high order TTI
float pxVx=0;float pzVx=0;float pxVz=0;float pzVz=0;
for(int in=0;in<N;in++)
{
pxVx+=cof[in]*(Vx[i+in+1][j]-Vx[i-in][j]);
pxVz+=cof[in]*(Vz[i+in][j]-Vz[i-in-1][j]);
pzVx+=cof[in]*(Vx[i][j+in+1]-Vx[i][j-in]);
pzVz+=cof[in]*(Vz[i][j+in]-Vz[i][j-in-1]);
}
Txx_x[i][j]=1.0/(1+0.5*dt*ddx[i][j])*((1-0.5*ddx[i][j]*dt)*Txx_x[i][j]+C_11[i][j]*dt/dx*pxVx+C_15[i][j]*dt/dx*pxVz);
Txx_z[i][j]=1.0/(1+0.5*dt*ddz[i][j])*((1-0.5*ddz[i][j]*dt)*Txx_z[i][j]+C_13[i][j]*dt/dz*pzVz+C_15[i][j]*dt/dz*pzVx);
Tzz_x[i][j]=1.0/(1+0.5*dt*ddx[i][j])*((1-0.5*ddx[i][j]*dt)*Tzz_x[i][j]+C_13[i][j]*dt/dx*pxVx+C_35[i][j]*dt/dx*pxVz);
Tzz_z[i][j]=1.0/(1+0.5*dt*ddz[i][j])*((1-0.5*ddz[i][j]*dt)*Tzz_z[i][j]+C_33[i][j]*dt/dz*pzVz+C_35[i][j]*dt/dz*pzVx);
Txx[i][j]=Txx_x[i][j]+Txx_z[i][j];
Tzz[i][j]=Tzz_x[i][j]+Tzz_z[i][j];
if(i==SX&&j==SZ)
{
float tmp=pow(PI*f0*(k*dt-t0),2);
//Ricker
Txx_x[i][j]+=1*exp(-1.0*tmp)*(1-2.0*tmp);
Txx_z[i][j]+=1*exp(-1.0*tmp)*(1-2.0*tmp);
Tzz_x[i][j]+=1*exp(-1.0*tmp)*(1-2.0*tmp);
Tzz_z[i][j]+=1*exp(-1.0*tmp)*(1-2.0*tmp);
//Gauss
//Tzz[i][j]+=-1.0*PI*PI*f0*f0*(k*dt-t0)*exp(-1.0*tmp)*(3.0-2.0*tmp);
//Txx[i][j]+=-1.0*PI*PI*f0*f0*(k*dt-t0)*exp(-1.0*tmp)*(3.0-2.0*tmp);
}
pxVx=0;pzVx=0;pxVz=0;pzVz=0;
for(int in=0;in<N;in++)
{
pxVx+=cof[in]*(Vx[i+in+1][j]-Vx[i-in][j]);
pxVz+=cof[in]*(Vz[i+in][j]-Vz[i-in-1][j]);
pzVx+=cof[in]*(Vx[i][j+in+1]-Vx[i][j-in]);
pzVz+=cof[in]*(Vz[i][j+in]-Vz[i][j-in-1]);
}
Txz_x[i][j]=1.0/(1+0.5*dt*ddx[i][j])*((1-0.5*ddx[i][j]*dt)*Txz_x[i][j]+C_15[i][j]*dt/dx*pxVx+C_55[i][j]*dt/dx*pxVz);
Txz_z[i][j]=1.0/(1+0.5*dt*ddz[i][j])*((1-0.5*ddz[i][j]*dt)*Txz_z[i][j]+C_35[i][j]*dt/dz*pzVz+C_55[i][j]*dt/dz*pzVx);
Txz[i][j]=Txz_x[i][j]+Txz_z[i][j];
}
}
for(i=N;i<NX-N;i++)
{
for(j=N;j<NZ-N;j++)
{
float pxTxx=0;float pzTxz=0;
for(int in=0;in<N;in++)
{
pxTxx+=cof[in]*(Txx[i+in][j]-Txx[i-in-1][j]);
pzTxz+=cof[in]*(Txz[i][j+in]-Txz[i][j-in-1]);
}
Vx_x[i][j]=1.0/(1+0.5*dt*ddx[i][j])*((1-0.5*ddx[i][j]*dt)*Vx_x[i][j]+dt/Rou[i][j]/dx*pxTxx);
Vx_z[i][j]=1.0/(1+0.5*dt*ddz[i][j])*((1-0.5*ddz[i][j]*dt)*Vx_z[i][j]+dt/Rou[i][j]/dz*pzTxz);
Vx[i][j]=Vx_x[i][j]+Vx_z[i][j];
//if(i==SX&&j==SZ)
//{
// float tmp=pow(PI*f0*(k*dt-t0),2);
// //Ricker
// Vz_x[i][j]+=1*exp(-1.0*tmp)*(1-2.0*tmp);
// Vz_z[i][j]+=1*exp(-1.0*tmp)*(1-2.0*tmp);
//}
float pxTxz=0;float pzTzz=0;
for(int in=0;in<N;in++)
{
pxTxz+=cof[in]*(Txz[i+in+1][j]-Txz[i-in][j]);
pzTzz+=cof[in]*(Tzz[i][j+in+1]-Tzz[i][j-in]);
}
Vz_x[i][j]=1.0/(1+0.5*dt*ddx[i][j])*((1-0.5*ddx[i][j]*dt)*Vz_x[i][j]+dt/Rou[i][j]/dx*pxTxz);
Vz_z[i][j]=1.0/(1+0.5*dt*ddz[i][j])*((1-0.5*ddz[i][j]*dt)*Vz_z[i][j]+dt/Rou[i][j]/dz*pzTzz);
Vz[i][j]=Vz_x[i][j]+Vz_z[i][j];
}
}
//for (i = 0; i < NX; i++)
for (i = pml; i < NX-pml; i++)
{
int rz=SZ;
data_vx[i][k]=Txx[i][rz]+Tzz[i][rz];
//data_vx[i][k]=Vx[i][rz];
data_vz[i][k]=Vz[i][rz];
}
if(k%200==0)
{
//FILE *fp121;
//char name[256];
//sprintf(name,"T_TTI2.dat%d",k);
//fp121=fopen(name, "wb+");
////for (i = 0; i < NX; i++)
//// for (j = 0; j < NZ; j++)
//for (i = pml; i < NX-pml; i++)
// for (j = pml; j < NZ-pml; j++)
// {
// float T=1.0/2*(Txx[i][j]+Tzz[i][j]);
// fwrite(&T, sizeof(float), 1, fp121);
// }
//fclose(fp121);
//FILE *fp122;
char name[256];
//sprintf(name,"Vx.dat%d",k);
//fp122=fopen(name, "wb+");
////for (i = 0; i < NX; i++)
//// for (j = 0; j < NZ; j++)
//for (i = pml; i < NX-pml; i++)
// for (j = pml; j < NZ-pml; j++)
// {
// fwrite(&Vx[i][j], sizeof(float), 1, fp122);
// }
//fclose(fp122);
FILE *fp123;
sprintf(name,"u.dat%d",k);
fp123=fopen(name, "wb+");
//for (i = 0; i < NX; i++)
// for (j = 0; j < NZ; j++)
for (i = pml; i < NX-pml; i++)
for (j = pml; j < NZ-pml; j++)
{
float u=Txx[i][j]+Tzz[i][j];
//fwrite(&Vz[i][j], sizeof(float), 1, fp123);
fwrite(&u, sizeof(float), 1, fp123);
}
fclose(fp123);
}
}
fp1=fopen("Txx.dat", "wb+");
for (i = pml; i < NX-pml; i++)
for (j = pml; j < NZ-pml; j++)
{
fwrite(&Txx[i][j], sizeof(float), 1, fp1);
}
fp2=fopen("Tzz.dat", "wb+");
for (i = pml; i < NX-pml; i++)
for (j = pml; j < NZ-pml; j++)
{
fwrite(&Tzz[i][j], sizeof(float), 1, fp2);
}
fp12=fopen("T.dat", "wb+");
for (i = pml; i < NX-pml; i++)
for (j = pml; j < NZ-pml; j++)
{
float T=1.0/2*(Txx[i][j]+Tzz[i][j]);
fwrite(&T, sizeof(float), 1, fp12);
}
fp3=fopen("Txz.dat", "wb+");
for (i = pml; i < NX-pml; i++)
for (j = pml; j < NZ-pml; j++)
{
fwrite(&Txz[i][j], sizeof(float), 1, fp3);
}
fp4=fopen("Vx.dat", "wb+");
for (i = pml; i < NX-pml; i++)
for (j = pml; j < NZ-pml; j++)
{
fwrite(&Vx[i][j], sizeof(float), 1, fp4);
}
fp5=fopen("Vz.dat", "wb+");
for (i = pml; i < NX-pml; i++)
for (j = pml; j < NZ-pml; j++)
{
fwrite(&Vz[i][j], sizeof(float), 1, fp5);
}
//fp6=fopen("data_vx.dat", "wb+");
fp6=fopen("uobs.dat", "wb+");
//for (i = 0; i < NX; i++)
for (i = pml; i < NX-pml; i++)
for (j = 0; j < NT; j++)
{
fwrite(&data_vx[i][j], sizeof(float), 1, fp6);
}
// fp7=fopen("data_vz.dat", "wb+");
// for (i = 0; i < NX; i++)
// for (j = 0; j < NT; j++)
// {
// fwrite(&data_vz[i][j], sizeof(float), 1, fp7);
// }
fp1=fopen("Vp.dat", "wb+");
for (i = pml; i < NX-pml; i++)
for (j = pml; j < NZ-pml; j++)
{
fwrite(&Vp[i][j], sizeof(float), 1, fp1);
}
//We should delete memory here!!!
}5.2 MATLAB代码
% Elastic Velocity-Stress Finite-difference Modeling with output PML in MATLAB
% Converted from C++ code provided by Zhang Jianming
% Constants
PI = 3.1415926;
dx = 10;
dz = 10;
pml = 20;
NX = 200+2*pml;
NZ = 200+2*pml;
NT = 801;
dt = 0.0005;
N = 6;
fi = (PI / 4.0);
% Allocate memory for matrices
Txx = zeros(NX, NZ);
Txx_x = zeros(NX, NZ);
Txx_z = zeros(NX, NZ);
Tzz = zeros(NX, NZ);
Tzz_x = zeros(NX, NZ);
Tzz_z = zeros(NX, NZ);
Txz = zeros(NX, NZ);
Txz_x = zeros(NX, NZ);
Txz_z = zeros(NX, NZ);
Vx = zeros(NX, NZ);
Vx_x = zeros(NX, NZ);
Vx_z = zeros(NX, NZ);
Vz = zeros(NX, NZ);
Vz_x = zeros(NX, NZ);
Vz_z = zeros(NX, NZ);
L = zeros(NX, NZ);
M = zeros(NX, NZ);
e = zeros(NX, NZ);
C11 = zeros(NX, NZ);
C33 = zeros(NX, NZ);
C44 = zeros(NX, NZ);
C66 = zeros(NX, NZ);
C13 = zeros(NX, NZ);
Rou = zeros(NX, NZ);
C_11 = zeros(NX, NZ);
C_13 = zeros(NX, NZ);
C_15 = zeros(NX, NZ);
C_33 = zeros(NX, NZ);
C_35 = zeros(NX, NZ);
C_55 = zeros(NX, NZ);
O = zeros(NX, NZ);
Vp = zeros(NX, NZ);
Eps = zeros(NX, NZ);
Del = zeros(NX, NZ);
Vs = zeros(NX, NZ);
Gam = zeros(NX, NZ);
F = zeros(NX, NZ);
data_vx = zeros(NX, NT);
data_vz = zeros(NX, NT);
% Initialize parameters
f0 = 15;
t0 = 1.2 / f0;
SX = floor(NX / 2);
SZ = floor(NZ / 2);
R = 0.001;
Vmax = 7500;
plx = pml * dx;
plz = pml * dz;
ddx = zeros(NX, NZ);
ddz = zeros(NX, NZ);
% Initialize model parameters
for i = 1:NX
for j = 1:NZ
Vp(i, j) = 3000;
Eps(i, j) = 0.4;
Del(i, j) = 0.2;
Vs(i, j) = 2000;
Gam(i, j) = 0.1;
%
% if j > 7.0 / 10.0 * NZ
% Vs(i, j) = 2800;
% end
%
% if j > 8.0 / 10.0 * NZ
% Vp(i, j) = 4000;
% end
%
Rou(i, j) = 3.44 * 10^3;
C11(i, j) = Rou(i, j) * (1.0 + 2 * Eps(i, j)) * Vp(i, j)^2;
C33(i, j) = Rou(i, j) * Vp(i, j)^2;
C44(i, j) = Rou(i, j) * Vs(i, j)^2;
C66(i, j) = Rou(i, j) * (1.0 + 2 * Gam(i, j)) * Vs(i, j)^2;
F(i, j) = 1.0 - Vs(i, j)^2 / Vp(i, j)^2;
C13(i, j) = Rou(i, j) * Vp(i, j)^2 * sqrt(F(i, j) * (F(i, j) + 2 * Del(i, j))) - Rou(i, j) * Vs(i, j)^2;
O(i, j) = fi;
C_11(i, j) = C11(i, j) * cos(O(i, j))^4 + C33(i, j) * sin(O(i, j))^4 + (2 * C13(i, j) + 4 * C44(i, j)) * sin(O(i, j))^2 * cos(O(i, j))^2;
C_13(i, j) = (C11(i, j) + C33(i, j) - 4 * C44(i, j)) * sin(O(i, j))^2 * cos(O(i, j))^2 + C13(i, j) * (sin(O(i, j))^4 + cos(O(i, j))^4);
C_15(i, j) = (C13(i, j) - C11(i, j) + 2 * C44(i, j)) * sin(O(i, j)) * cos(O(i, j))^3 - (C13(i, j) - C33(i, j) + 2 * C44(i, j)) * sin(O(i, j))^3 * cos(O(i, j));
C_33(i, j) = C11(i, j) * sin(O(i, j))^4 + C33(i, j) * cos(O(i, j))^4 + (2 * C13(i, j) + 4 * C44(i, j)) * sin(O(i, j))^2 * cos(O(i, j))^2;
C_35(i, j) = (C13(i, j) - C11(i, j) + 2 * C44(i, j)) * sin(O(i, j))^3 * cos(O(i, j)) - (C13(i, j) - C33(i, j) + 2 * C44(i, j)) * sin(O(i, j)) * cos(O(i, j))^3;
C_55(i, j) = (C11(i, j) + C33(i, j) - 2 * C13(i, j)) * sin(O(i, j))^2 * cos(O(i, j))^2 + C44(i, j) * (cos(O(i, j))^2 - sin(O(i, j))^2)^2;
end
end
% PML setup
for i = 1:NX
for j = 1:NZ
if i <= pml && j <= pml
x = pml - i;
z = pml - j;
ddx(i, j) = -log(R) * 3 * Vmax * x^2 / (2 * plx^2);
ddz(i, j) = -log(R) * 3 * Vmax * z^2 / (2 * plz^2);
elseif i <= pml && j > NZ - pml
x = pml - i;
z = j - (NZ - pml);
ddx(i, j) = -log(R) * 3 * Vmax * x^2 / (2 * plx^2);
ddz(i, j) = -log(R) * 3 * Vmax * z^2 / (2 * plz^2);
elseif i > NX - pml && j <= pml
x = i - (NX - pml);
z = pml - j;
ddx(i, j) = -log(R) * 3 * Vmax * x^2 / (2 * plx^2);
ddz(i, j) = -log(R) * 3 * Vmax * z^2 / (2 * plz^2);
elseif i > NX - pml && j > NZ - pml
x = i - (NX - pml);
z = j - (NZ - pml);
ddx(i, j) = -log(R) * 3 * Vmax * x^2 / (2 * plx^2);
ddz(i, j) = -log(R) * 3 * Vmax * z^2 / (2 * plz^2);
elseif i > pml && i <= NX - pml && j <= pml
z = pml - j;
ddx(i, j) = 0;
ddz(i, j) = -log(R) * 3 * Vmax * z^2 / (2 * plz^2);
elseif i > pml && i <= NX - pml && j > NZ - pml
z = j - (NZ - pml);
ddx(i, j) = 0;
ddz(i, j) = -log(R) * 3 * Vmax * z^2 / (2 * plz^2);
elseif i <= pml && j > pml && j <= NZ - pml
x = pml - i;
ddx(i, j) = -log(R) * 3 * Vmax * x^2 / (2 * plx^2);
ddz(i, j) = 0;
elseif i > NX - pml && j > pml && j <= NZ - pml
x = i - (NX - pml);
ddx(i, j) = -log(R) * 3 * Vmax * x^2 / (2 * plx^2);
ddz(i, j) = 0;
else
ddx(i, j) = 0;
ddz(i, j) = 0;
end
end
end
% Coefficients for finite difference
cof = zeros(1, N);
if N == 1
cof(1) = 1.0;
elseif N == 2
cof = [1.125, -0.041666667];
elseif N == 3
cof = [1.171875, -0.065104167, 0.0046875];
elseif N == 4
cof = [1.196289, -0.0797526, 0.009570313, -0.0006975447];
elseif N == 5
cof = [1.2112427, -0.08972168, 0.013842773, -0.0017656599, 0.00011867947];
elseif N == 6
cof = [1.2213364, -0.096931458, 0.017447662, -0.0029672895, 0.00035900540, -0.000021847812];
elseif N == 7
cof = [1.2286062, -0.10238385, 0.02047677, -0.0041789327, 0.00068945355, -0.000076922503, 0.0000042365148];
elseif N == 8
cof = [1.2340911, -0.10664985, 0.023036367, -0.0053423856, 0.0010772712, -0.00016641888, 0.000017021711, -0.00000085234642];
end
% Main time loop
for k = 1:NT
% Update stresses
for i = N+1:NX-N
for j = N+1:NZ-N
pxVx = 0; pzVx = 0; pxVz = 0; pzVz = 0;
for in = 0:N-1
pxVx = pxVx + cof(in+1) * (Vx(i+in+1,j) - Vx(i-in,j));
pxVz = pxVz + cof(in+1) * (Vz(i+in,j) - Vz(i-in-1,j));
pzVx = pzVx + cof(in+1) * (Vx(i,j+in+1) - Vx(i,j-in));
pzVz = pzVz + cof(in+1) * (Vz(i,j+in) - Vz(i,j-in-1));
end
Txx_x(i,j) = 1.0 / (1 + 0.5 * dt * ddx(i,j)) * ((1 - 0.5 * ddx(i,j) * dt) * Txx_x(i,j) + C_11(i,j) * dt / dx * pxVx + C_15(i,j) * dt / dx * pxVz);
Txx_z(i,j) = 1.0 / (1 + 0.5 * dt * ddz(i,j)) * ((1 - 0.5 * ddz(i,j) * dt) * Txx_z(i,j) + C_13(i,j) * dt / dz * pzVz + C_15(i,j) * dt / dz * pzVx);
Tzz_x(i,j) = 1.0 / (1 + 0.5 * dt * ddx(i,j)) * ((1 - 0.5 * ddx(i,j) * dt) * Tzz_x(i,j) + C_13(i,j) * dt / dx * pxVx + C_35(i,j) * dt / dx * pxVz);
Tzz_z(i,j) = 1.0 / (1 + 0.5 * dt * ddz(i,j)) * ((1 - 0.5 * ddz(i,j) * dt) * Tzz_z(i,j) + C_33(i,j) * dt / dz * pzVz + C_35(i,j) * dt / dz * pzVx);
Txx(i,j) = Txx_x(i,j) + Txx_z(i,j);
Tzz(i,j) = Tzz_x(i,j) + Tzz_z(i,j);
% Source term
if i == SX && j == SZ
tmp = (PI * f0 * (k * dt - t0))^2;
Txx_x(i,j) = Txx_x(i,j) + exp(-tmp) * (1 - 2 * tmp);
Txx_z(i,j) = Txx_z(i,j) + exp(-tmp) * (1 - 2 * tmp);
Tzz_x(i,j) = Txx_x(i,j);
Tzz_z(i,j) = Txx_z(i,j);
end
pxVx = 0; pzVx = 0; pxVz = 0; pzVz = 0;
for in = 0:N-1
pxVx = pxVx + cof(in+1) * (Vx(i+in+1,j) - Vx(i-in,j));
pxVz = pxVz + cof(in+1) * (Vz(i+in,j) - Vz(i-in-1,j));
pzVx = pzVx + cof(in+1) * (Vx(i,j+in+1) - Vx(i,j-in));
pzVz = pzVz + cof(in+1) * (Vz(i,j+in) - Vz(i,j-in-1));
end
Txz_x(i,j) = 1.0 / (1 + 0.5 * dt * ddx(i,j)) * ((1 - 0.5 * ddx(i,j) * dt) * Txz_x(i,j) + C_15(i,j) * dt / dx * pxVx + C_55(i,j) * dt / dx * pxVz);
Txz_z(i,j) = 1.0 / (1 + 0.5 * dt * ddz(i,j)) * ((1 - 0.5 * ddz(i,j) * dt) * Txz_z(i,j) + C_35(i,j) * dt / dz * pzVz + C_55(i,j) * dt / dz * pzVx);
Txz(i,j) = Txz_x(i,j) + Txz_z(i,j);
end
end
% Update velocities
for i = N+1:NX-N
for j = N+1:NZ-N
pxTxx = 0; pzTxz = 0;
for in = 0:N-1
pxTxx = pxTxx + cof(in+1) * (Txx(i+in,j) - Txx(i-in-1,j));
pzTxz = pzTxz + cof(in+1) * (Txz(i,j+in) - Txz(i,j-in-1));
end
Vx_x(i,j) = 1.0 / (1 + 0.5 * dt * ddx(i,j)) * ((1 - 0.5 * ddx(i,j) * dt) * Vx_x(i,j) + dt / Rou(i,j) / dx * pxTxx);
Vx_z(i,j) = 1.0 / (1 + 0.5 * dt * ddz(i,j)) * ((1 - 0.5 * ddz(i,j) * dt) * Vx_z(i,j) + dt / Rou(i,j) / dz * pzTxz);
Vx(i,j) = Vx_x(i,j) + Vx_z(i,j);
pxTxz = 0; pzTzz = 0;
for in = 0:N-1
pxTxz = pxTxz + cof(in+1) * (Txz(i+in+1,j) - Txz(i-in,j));
pzTzz = pzTzz + cof(in+1) * (Tzz(i,j+in+1) - Tzz(i,j-in));
end
Vz_x(i,j) = 1.0 / (1 + 0.5 * dt * ddx(i,j)) * ((1 - 0.5 * ddx(i,j) * dt) * Vz_x(i,j) + dt / Rou(i,j) / dx * pxTxz);
Vz_z(i,j) = 1.0 / (1 + 0.5 * dt * ddz(i,j)) * ((1 - 0.5 * ddz(i,j) * dt) * Vz_z(i,j) + dt / Rou(i,j) / dz * pzTzz);
Vz(i,j) = Vz_x(i,j) + Vz_z(i,j);
end
end
% Plot the wavefield for animation
ndt = 10;
if k>=200 & mod(k, ndt) == 0
TT=Txx(pml+1:NX-pml,pml+1:NZ-pml)+Tzz(pml+1:NX-pml,pml+1:NZ-pml);
imagesc(TT);
colormap('jet');
colorbar;
% caxis([-1, 1]);
title(['Wavefield at time step: ', num2str(k)]);
xlabel('X');
ylabel('Z');
drawnow;
frame = getframe(gcf);
im = frame2im(frame);
[imind, cm] = rgb2ind(im, 256);
if k == 200
imwrite(imind, cm, 'Wavefield.gif', 'gif', 'Loopcount', inf, 'DelayTime', 0.1);
else
imwrite(imind, cm, 'Wavefield.gif', 'gif', 'WriteMode', 'append', 'DelayTime', 0.1);
end
end
% Record data
for i = 1:NX
rz = SZ;
data_vx(i,k) = Vx(i,rz);
data_vz(i,k) = Vz(i,rz);
end
% % Save data every 1000 time steps
% if mod(k, 1000) == 0
% Vx_filename = sprintf('Vx_%d.dat', k);
% Vz_filename = sprintf('Vz_%d.dat', k);
% save(Vx_filename, 'Vx', '-ascii');
% save(Vz_filename, 'Vz', '-ascii');
% end
end
% % Save final data
% save('Txx.dat', 'Txx', '-ascii');
% save('Tzz.dat', 'Tzz', '-ascii');
% T = 0.5 * (Txx + Tzz);
% save('T.dat', 'T', '-ascii');
% save('Txz.dat', 'Txz', '-ascii');
% save('Vx.dat', 'Vx', '-ascii');
% save('Vz.dat', 'Vz', '-ascii');
% save('data_vx.dat', 'data_vx', '-ascii');
% save('data_vz.dat', 'data_vz', '-ascii');
% save('Vp.dat', 'Vp', '-ascii');
% % Plot the wavefield
% imagesc(Vx);
% colormap('jet');
% colorbar;
% title('Vx Wavefield');
% xlabel('X');
% ylabel('Z');








 博客围绕波动方程有限差分法模拟展开,强调了稳定性和频散、震源设置、弹性波转换、PML边界等关键问题,给出了原理说明。还提供了C/C++和MATLAB代码,并展示了多个数值算例,最后给出PML外置的补充代码。
博客围绕波动方程有限差分法模拟展开,强调了稳定性和频散、震源设置、弹性波转换、PML边界等关键问题,给出了原理说明。还提供了C/C++和MATLAB代码,并展示了多个数值算例,最后给出PML外置的补充代码。

















 1506
1506










