(Leetcode) 鸡蛋掉落 - Python实现

最新推荐文章于 2025-07-15 16:19:48 发布

原创最新推荐文章于 2025-07-15 16:19:48 发布 · 1.1k 阅读

5 ·

CC 4.0 BY-SA版权

Leetcode 专栏收录该内容

72 篇文章

订阅专栏

本文解析了一个经典的动态规划问题——鸡蛋掉落问题。通过构建二维数组dp，推导出状态方程，给出了确定任意楼层中鸡蛋破碎临界点所需最少投掷次数的算法实现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目：鸡蛋掉落

你将获得 K 个鸡蛋，并可以使用一栋从 1 到 N 共有 N 层楼的建筑。

每个蛋的功能都是一样的，如果一个蛋碎了，你就不能再把它掉下去。

你知道存在楼层 F ，满足 0 <= F <= N 任何从高于 F 的楼层落下的鸡蛋都会碎，从 F 楼层或比它低的楼层落下的鸡蛋都不会破。

每次移动，你可以取一个鸡蛋（如果你有完整的鸡蛋）并把它从任一楼层 X 扔下（满足 1 <= X <= N）。

你的目标是确切地知道 F 的值是多少。

无论 F 的初始值如何，你确定 F 的值的最小移动次数是多少？

示例：

输入：K = 1, N = 2，输出：2
解释：
鸡蛋从 1 楼掉落。如果它碎了，我们肯定知道 F = 0 。
否则，鸡蛋从 2 楼掉落。如果它碎了，我们肯定知道 F = 1 。
如果它没碎，那么我们肯定知道 F = 2 。
因此，在最坏的情况下我们需要移动 2 次以确定 F 是多少。

输入：K = 2, N = 6，输出：3

输入：K = 3, N = 14，输出：4
--------------------------------------------------------------------------------------

思路：此题来源是Google的算法面试题，是一个典型的动态规划问题。

首先，根据题设，我们可以知道的是，鸡蛋在某一楼层摔破和没有摔破，可以提供的信息是：没有摔破，表示需要往上层找，直到找到一个摔破的楼层；谁摔破了需要往下层找，知道找到一个没有摔破的楼层。

令二维数组dp[K][Step], K表示鸡蛋个数，Step表示第几次摔落。dp[i][j] 表示 i 个鸡蛋经过 j 次摔落最多可以确定多少层楼。

显然 j <= N。求d[i][j]：
当第j次摔落，鸡蛋不破，我们可以继续往上确定 dp[i][j -1] 层
当第j次摔落，鸡蛋破了，我们最多只能确定 dp[i -1][j -1] 层
状态方程 d[i][j] = dp[i-1][j -1] + (dp[i][j -1] + 1) 最后的1表示本层

解法：

class Solution(object):
    def superEggDrop(self, K, N):
        # 构建二维数组dp
        dp = [[0 for _ in range(N + 1)] for _ in range(K + 1)]
        for i in range(1, K + 1):
            for step in range(1, N + 1):
                dp[i][step] = dp[i - 1][step - 1] + (dp[i][step - 1] + 1)
                if dp[K][step] >= N:
                    return step
        return 0

参考：

https://www.cnblogs.com/yunlambert/p/10028865.html

https://blog.youkuaiyun.com/qq_35170267/article/details/84330662

补充Google原题：

一幢 200 层的大楼，给你两个鸡蛋。如果在第 n 层扔下鸡蛋，鸡蛋不碎，那么从第 n-1 层扔鸡蛋，都不碎。这两只鸡蛋一模一样，不碎的话可以扔无数次。最高从哪层楼扔下时鸡蛋不会碎？

解答：

因为有两个鸡蛋，所以我们可以考虑粗调和细调，即通过第一个鸡蛋的试错来缩小答案的范围。比如第一个鸡蛋在k层碎了，那么我们就可以确定临界楼层是[1，k)[1，k)之间；所以我们首先考虑的应该就是第一个鸡蛋应该在哪里扔。

假设第一个鸡蛋的楼层策略是k1，k2,k3....kpk1，k2,k3....kp，其中p是扔的总次数，楼高为N

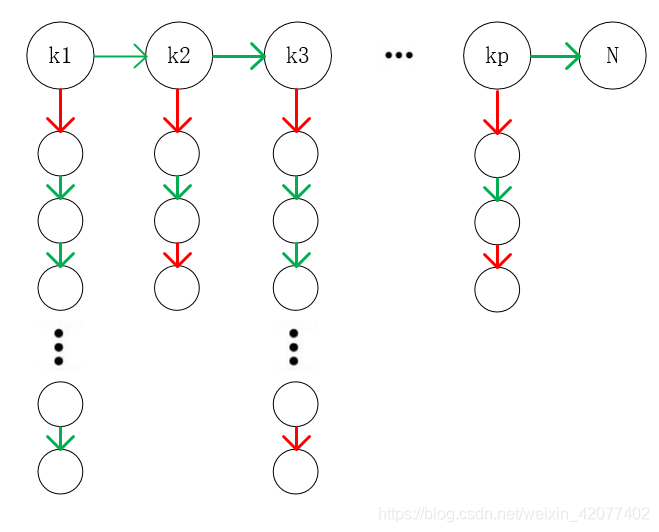
第二个鸡蛋肯定是在ki之间进行遍历，所以优化这个问题就是求一个策略组合使得p的值最小。举个例子，如果我们用二分法，选了k1=50扔，没有碎，好的我们进入下一个状态，取k2=75，仍然没有碎，进入下一个状态k3=90，碎了，说明临界不碎楼层是在[76，89][76，89]之间的，我们总共实验了3+14=17次。我们这里选用二分法的k1、k2、k3就是一种可选的策略，换成其他的也可以，但是要使这个策略的p尽量的小就是我们的目标。

所以我们再仔细观察一下上图，发现小圆圈其实都是第二个鸡蛋遍历的过程，都是O(n)，所以可以等价为一个操作，这个图实际上也就是一个树形结构:

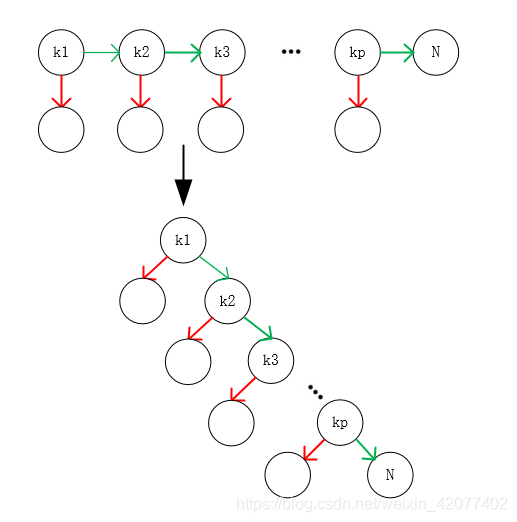
如果这个树类似下面的结构的话，我们可以得到最优解:

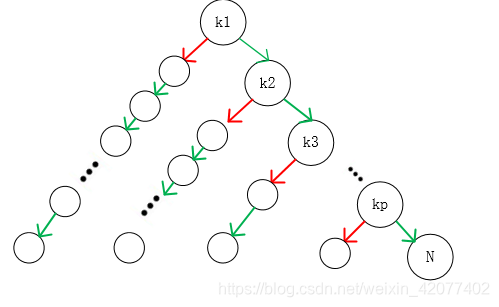
我们的树结构最好满足的关系为:

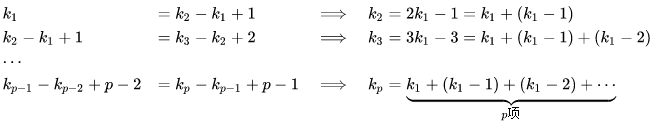
我们来解析一下第一个式子:k1=k2−k1+1k1=k2−k1+1,这是因为k1−1=(k2−k1−1)+1k1−1=(k2−k1−1)+1,加1是因为k2这个节点。要满足每棵子树的树高相等，kpkp必须是一个递减等差数列。所以我们可以令kp∼Nkp∼N，所以就有k1(k1+1)2=Nk1(k1+1)2=N

回到Google这道面试题上来的话，就是x()(x+1)2=200x()(x+1)2=200,解得x=14x=14，所以扔蛋的一种策略为14，27，39，50，60，69，77，84，90，95，99，一共需要尝试11+(13+12+11+10+9+8+7+6+5+4)/10=11+8.5 -->=20次。