线性表基础：栈（四）经典面试题（栈结构扩展应⽤ part2）

经典面试题 - 栈结构扩展应⽤

推荐刷题顺序：
LeetCode #20 有效的括号
LeetCode #1021 删除最外层的括号
LeetCode #1249 移除⽆效的括号
LeetCode #145 ⼆叉树的后序遍历
LeetCode #331 验证⼆叉树的前序序列化
LeetCode #227 基本计算器II

5. LeetCode #331 验证⼆叉树的前序序列化

题目描述：
序列化二叉树的一种方法是使用前序遍历。当我们遇到一个非空节点时，我们可以记录下这个节点的值。如果它是一个空节点，我们可以使用一个标记值记录，例如 #。

例如，上面的二叉树可以被序列化为字符串 “9,3,4,#,#,1,#,#,2,#,6,#,#”，其中 # 代表一个空节点。

给定一串以逗号分隔的序列，验证它是否是正确的二叉树的前序序列化。编写一个在不重构树的条件下的可行算法。

每个以逗号分隔的字符或为一个整数或为一个表示 null 指针的 ‘#’ 。

你可以认为输入格式总是有效的，例如它永远不会包含两个连续的逗号，比如 “1,,3” 。

解题思路：
思路1：每次拆掉⼀个“数字，#，#”的节点（即叶⼦结点），最后树上的全部节点都会被拆光（最终只剩⼀个“#”），能拆光的序列就是合法序列。

4##看成是一个# — 93#1##2#6##
1##看成是一个# — 93##2#6##
3##看成是一个# — 9#2#6##
6##看成是一个# — 9#2##
2##看成是一个# — 9##
9##看成是一个# — #

class Solution {
    public boolean isValidSerialization(String preorder) {
        String[] split = preorder.split(",");
        String[] temp = new String[split.length];
        int j = 0;
        for (int i = 0; i < split.length; i++) {
            temp[j++] = split[i];
            //超过3个字符以后，倒数三个字符是 数字## 形式则 转换为一个 #
            while (j > 2 && !temp[j - 3].equals("#") && temp[j - 2].equals("#") && temp[j - 1].equals("#")) {
                temp[j - 3] = "#";
                j -= 2;
            }
        }
        return j == 1 && temp[0].equals("#");
    }
}

思路2：我们可以定义一个概念，叫做槽位。一个槽位可以被看作「当前二叉树中正在等待被节点填充」的那些位置。

二叉树的建立也伴随着槽位数量的变化。每当遇到一个节点时：

• 如果遇到了空节点，则要消耗一个槽位；
• 如果遇到了非空节点，则除了消耗一个槽位外，还要再补充两个槽位。

此外，还需要将根节点作为特殊情况处理（初始状态有⼀个槽位）。

合法的⼆叉树前序遍历最后会刚好⽤完所有的槽位。否则若槽位多了，或者在遍历的过程中槽位数量不足，则序列不合法。

class Solution {
    public boolean isValidSerialization(String preorder) {
        int slot = 1;// 初始槽位为1
        for (String s : preorder.split(",")) {
            if(slot == 0) return false;
            if (s.equals("#")) {
                slot--;
            } else {
                slot++;// slots = slots - 1 + 2
            }
        }
        return slot == 0;
    }
}

字符串的效率慢一点

class Solution {
    public boolean isValidSerialization(String preorder) {
        int slot = 1;// 初始槽位为1
        int i = 0;
        int length = preorder.length();
        while (i < length) {
            if (slot == 0) return false;
            if (preorder.charAt(i) == ',') {
                i++;
            } else if (preorder.charAt(i) == '#') {
                i++;
                slot--;
            } else {
                // 数字，有可能是多位数
                while (i < length && preorder.charAt(i) != ',') {
                    i++;
                }
                slot++;// slots = slots - 1 + 2
            }
        }
        return slot == 0;
    }
}

6. LeetCode #227 基本计算器II

题目描述：
给你一个字符串表达式 s ，请你实现一个基本计算器来计算并返回它的值。
整数除法仅保留整数部分。

解题思路：
思路1：找到式⼦中优先级最低的运算符，然后递归分治运算两侧的⼦式即可。（栈篇章第一节末尾已经实现过一个类似的了）

思路2：
由于乘除优先于加减计算，因此不妨考虑先进行所有乘除运算，并将这些乘除运算后的整数值放回原表达式的相应位置，则随后整个表达式的值，就等于一系列整数加减后的值。

基于此，我们可以用一个栈，保存这些（进行乘除运算后的）整数的值。对于加减号后的数字，将其直接压入栈中；对于乘除号后的数字，可以直接与栈顶元素计算，并替换栈顶元素为计算后的结果。

具体来说，遍历字符串 s，并用变量 preSign 记录每个数字之前的运算符，对于第一个数字，其之前的运算符视为加号。每次遍历到数字末尾时，根据 preSign 来决定计算方式：

• 加号：将数字压入栈；
• 减号：将数字的相反数压入栈；
• 乘除号：计算数字与栈顶元素，并将栈顶元素替换为计算结果。

代码实现中，若读到一个运算符，或者遍历到字符串末尾，即认为是遍历到了数字末尾。处理完该数字后，更新 preSign 为当前遍历的字符。

遍历完字符串 s 后，将栈中元素累加，即为该字符串表达式的值。

动画演示：
遍历表达式，第一个数字，其之前的运算符视为加号

第一个数字是3，前面的运算符是+号，直接将数字压入栈
第二个数字4同理，前面的运算符是+号，直接将数字压入栈

接着走遇到乘号更新到preSign：

数字2前面的运算符是乘号，所以直接计算该数字与栈顶元素，并将栈顶元素替换为计算结果

继续走更新符号为-号，遇到数字6时，将数字的相反数压入栈：

继续走更新符号为除号，遇到数字2时，直接计算该数字与栈顶元素，并将栈顶元素替换为计算结果：

最后遍历完字符串后，将栈中元素相加即可。

class Solution {
    public int calculate(String s) {
        s += '@';//加一个特殊符号，简化代码临界条件判断
        Character preSign = '+';
        LinkedList<Integer> numStack = new LinkedList<>();
        int num = 0;
        for (char c : s.toCharArray()) {
            if (c == ' ') continue;
            if (Character.isDigit(c)) {
                num = num * 10 + c - '0';
                continue;
            }
            // 当前是操作符，根据前一个操作符决定操作
            switch (preSign) {
                case '+':
                    numStack.push(num);
                    break;
                case '-':
                    numStack.push(-num);
                    break;
                case '*':
                    numStack.push(numStack.pop() * num);
                    break;
                case '/':
                    numStack.push(numStack.pop() / num);
                    break;
            }
            num = 0;
            preSign = c;
        }
        int result = 0;
        while (!numStack.isEmpty()) {
            result += numStack.pop();
        }
        return result;
    }
}

思路3：使⽤操作数栈和运算符栈辅助计算，当运算符栈遇到更低优先级的运算符时，可以将之前更⾼优先级的运算符对应的结果计算出来。

我们可以把3 + 2 * 2 ，看成是( 3 + ( 2 * 2 ) ) ，然后拆成两条线思维逻辑：

• 操作符视角：
  左括号代表压入，右括号代表弹出并计算
  

• 操作数视角：
  对应相关位置的操作数，先压入3，再压入2，再压入2，遇到右括号弹出2个2完成计算将结果压回栈，最后弹出2个2的结果再弹出3完成计算
  

• +号的优先级小于*号：
  

  通过这种思维方式，如果我们去掉括号，依次性把每个运算符和操作数压入栈里后，当新压入的运算符优先级要小于等于栈顶元素运算符优先级的时候，就先把前面这个运算符的运算结果先计算出来

• 另外对于有括号的情况，左括号相当于提⾼了内部全部运算符的优先级，因此我们可以设定一个优先级基准值，初始为0，每遇到一个左括号就给这个基准值增加100，每遇到一个右括号就给这个基准值减少100。而所有的运算符都是基于基准值进行计算的，定义+号优先级为基准值+1，*号优先级为基准值+2：
  

动画演示：

遍历表达式，遇到数字放入操作数栈，遇到运算符放入运算符栈，当遍历到第一个+号到时候：

如图当准备压入+符号发现优先级比栈顶元素乘号低，就先把乘号弹栈，并从操作数栈中弹出两个元素进行计算，最后把计算结果压回数字栈，然后再把+号压入运算符栈：

接着再压入3，乘号，因为乘号优先级高于栈顶的+号，所以直接入栈：

接着遇到左括号，基准值增加100，继续压入4和加号，此时加号的优先级就为101，因为优先级高于栈顶的乘号，也是直接入栈：

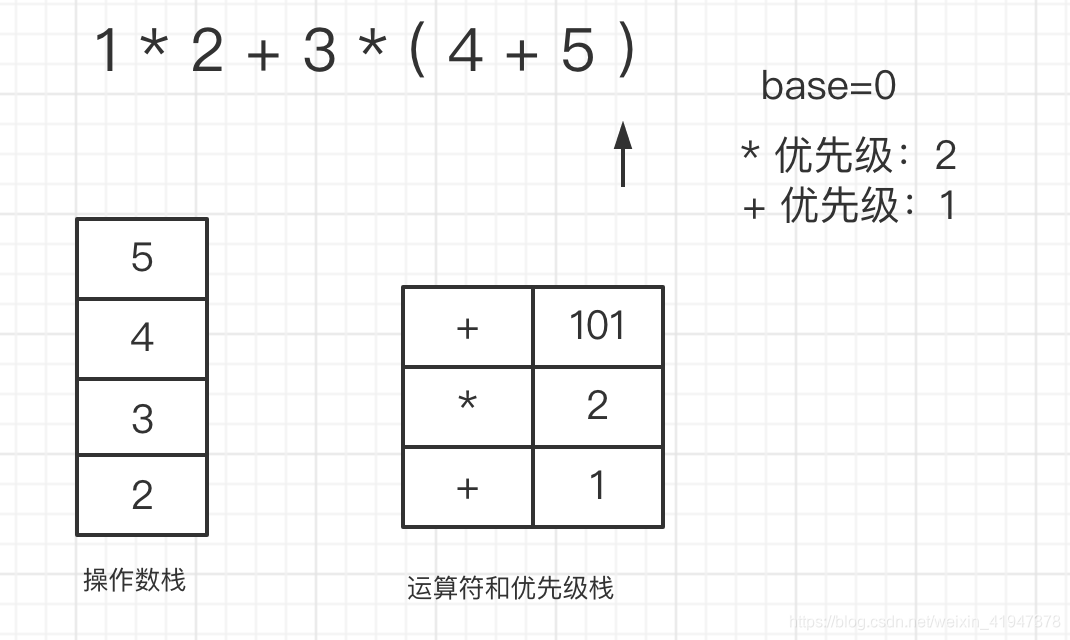
继续压入数字5，遇到右括号基准值减100：

最后只需要清空两个栈即可，依次弹出每个运算符和2个操作数计算，把计算结果再压回数字栈，然后再弹出操作符，2个操作数计算…直到运算符栈为空

运算符栈弹出+号，操作数栈弹出5和4，4+5=9：

运算符栈弹出乘号，操作数栈弹出9和3，3*9=27：

运算符栈弹出+号，操作数栈弹出27和2，2+27=29：

最后处在操作数栈中就一个数字了，这个数字就是表达式的计算结果

• 另外当表达式遍历完以后再开始清空两个栈的方式，可以用一个小技巧简化：通过给表达式末尾添加⼀个特殊操作符，设为最低优先级，当遇到最后一个操作符的时候因为优先级最低，就会把前面所有的操作符计算出来，可以简化代码边界条件的判断。

class Solution {
    public int calculate(String s) {
        LinkedList<Character> operateStack = new LinkedList<>();// 运算符栈
        LinkedList<Integer> operatePriorityStack = new LinkedList<>();// 运算符对应优先级
        Stack<Integer> numStack = new Stack<>();// 操作数栈
        s = s + '@';// 加上一个特殊运算符，因为@运算符优先级最低，所以遍历到最后@时会把前面所有运算符全都算掉，帮助我们简化代码的
        int num = 0;// 用来收集数字
        int cnt = 0;// 统计左右括号差值
        for (int i = 0; i < s.length(); i++) {
            char c = s.charAt(i);
            if (c == ' ') {
                continue;
            }
            if (c == '(') {
                cnt++;
                continue;
            }
            if (c == ')') {
                cnt--;
                continue;
            }
            if (getPriority(c, cnt) == -1) {
                num = num * 10 + c - '0';
                continue;
            }
            // 走到这说明当前是运算符
            numStack.push(num);// 之前统计的数字入操作数栈
            num = 0;
            // 当前操作符优先级 小于等于 栈顶的操作符优先级则计算
            int curPriority = getPriority(c, cnt);
            while (!operateStack.isEmpty() && (curPriority <= operatePriorityStack.peek())) {
                Integer num2 = numStack.pop();
                Integer num1 = numStack.pop();
                Character operate = operateStack.pop();
                operatePriorityStack.pop();
                numStack.push(operate(operate, num1, num2));// 计算并将结果push到操作数栈中
            }
            operateStack.push(c);// 压入新运算符
            operatePriorityStack.push(curPriority);// 压入新运算符对应的优先级
        }
        // 如果没@运算符，除了这个循环还需要特殊处理一下，把栈清空
        return numStack.pop();
    }

    private Integer operate(Character operate, Integer num1, Integer num2) {
        switch (operate) {
            case '+':
                return num1 + num2;
            case '-':
                return num1 - num2;
            case '*':
                return num1 * num2;
            case '/':
                return num1 / num2;
        }
        return 0;
    }

    private int getPriority(char c, int cnt) {
        int base = 100 * cnt;
        switch (c) {
            case '@':
                return 0;
            case '+':
            case '-':
                return 1 + base;
            case '*':
            case '/':
                return 2 + base;
            default:
                // 说明是数字
                return -1;
        }
    }
}

当然这道题题实际上没有这么复杂，因为题目给的表达式是没有左右括号的，主要是为了锻炼编码能力。