线性表基础：栈（三）经典面试题（栈结构扩展应⽤ part1）

经典面试题 - 栈结构扩展应⽤

推荐刷题顺序：
LeetCode #20 有效的括号
LeetCode #1021 删除最外层的括号
LeetCode #1249 移除⽆效的括号
LeetCode #145 ⼆叉树的后序遍历
LeetCode #331 验证⼆叉树的前序序列化
LeetCode #227 基本计算器II

1. LeetCode #20 有效的括号

题目描述：
给定一个只包括 ‘(’，’)’，’{’，’}’，’[’，’]’ 的字符串 s ，判断字符串是否有效。

有效字符串需满足：

• 左括号必须用相同类型的右括号闭合。
• 左括号必须以正确的顺序闭合。

解题思路：
判断括号的有效性可以使用「栈」这一数据结构来解决。

• 我们遍历给定的字符串 s。当我们遇到一个左括号时，我们会期望在后续的遍历中，有一个相同类型的右括号将其闭合。由于后遇到的左括号要先闭合，因此我们可以将这个左括号放入栈顶。
• 当我们遇到一个右括号时，我们需要将一个相同类型的左括号闭合。此时，我们可以取出栈顶的左括号并判断它们是否是相同类型的括号。如果不是相同的类型，或者栈中并没有左括号，那么字符串 s 无效，返回 False。为了快速判断括号的类型，我们可以使用哈希表存储每一种括号。哈希表的键为右括号，值为相同类型的左括号。
• 在遍历结束后，如果栈中没有左括号，说明我们将字符串 s 中的所有左括号闭合，返回 True，否则返回 False。
• 注意到有效字符串的长度一定为偶数，因此如果字符串的长度为奇数，我们可以直接返回 False，省去后续的遍历判断过程。

class Solution {
    public boolean isValid(String s) {
        int n = s.length();
        if (n % 2 == 1) {
            return false;
        }
        HashMap<Character, Character> mapping = new HashMap<>();
        mapping.put(')', '(');
        mapping.put('}', '{');
        mapping.put(']', '[');
        LinkedList<Character> stack = new LinkedList<>();
        for (char c : s.toCharArray()) {
            switch (c) {
                // 左括号入栈
                case '(':
                case '{':
                case '[':
                    stack.push(c);
                    break;
                case ')':
                case '}':
                case ']':
                    // 右括号和栈顶元素进行匹配
                    if (stack.isEmpty() || stack.peek() != mapping.get(c)) return false;
                    // 匹配成功出栈
                    stack.pop();
                    break;
            }
        }
        // 最终栈为空说明是合法字符串
        return stack.isEmpty();
    }
}

2. LeetCode #1021 删除最外层的括号

题目描述：
有效括号字符串为空 ("")、"(" + A + “)” 或 A + B，其中 A 和 B 都是有效的括号字符串，+ 代表字符串的连接。例如，""，"()"，"(())()" 和 “(()(()))” 都是有效的括号字符串。

如果有效字符串 S 非空，且不存在将其拆分为 S = A+B 的方法，我们称其为原语（primitive），其中 A 和 B 都是非空有效括号字符串。

给出一个非空有效字符串 S，考虑将其进行原语化分解，使得：S = P_1 + P_2 + … + P_k，其中 P_i 是有效括号字符串原语。

对 S 进行原语化分解，删除分解中每个原语字符串的最外层括号，返回 S 。

解题思路：
用栈模拟，遇到"（ “入栈，遇到” ）"出栈：

• 在入栈过程中当栈中元素个数>=1时说明当前遍历的左括号不是最外层括号，进行拼接
• 在出栈的过程中当栈中元素个数>=2时说明当前遍历的右括号不是最外层括号，进行拼接

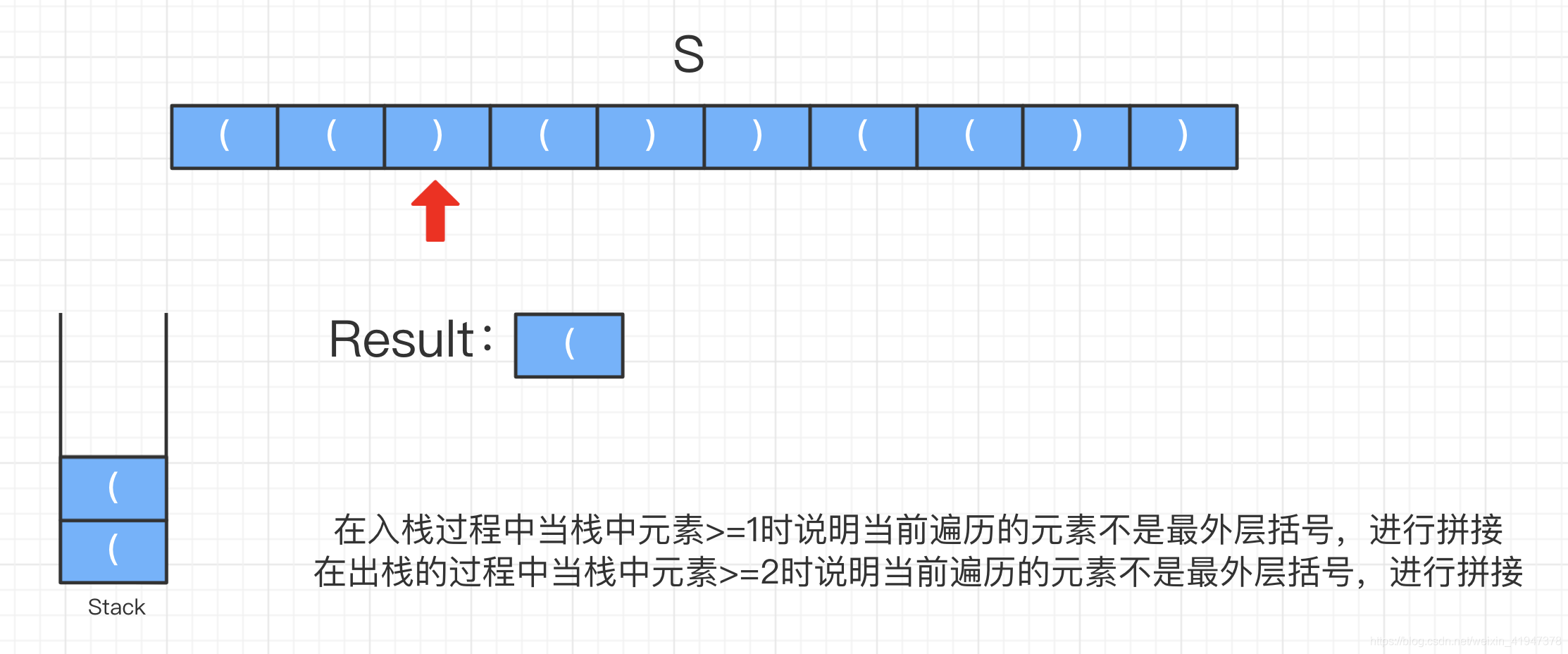
遍历第一个元素，“(”要进行入栈，发现栈中是空，说明此时遍历的是最外层括号需要删除，所以我们仅仅进行入栈操作。

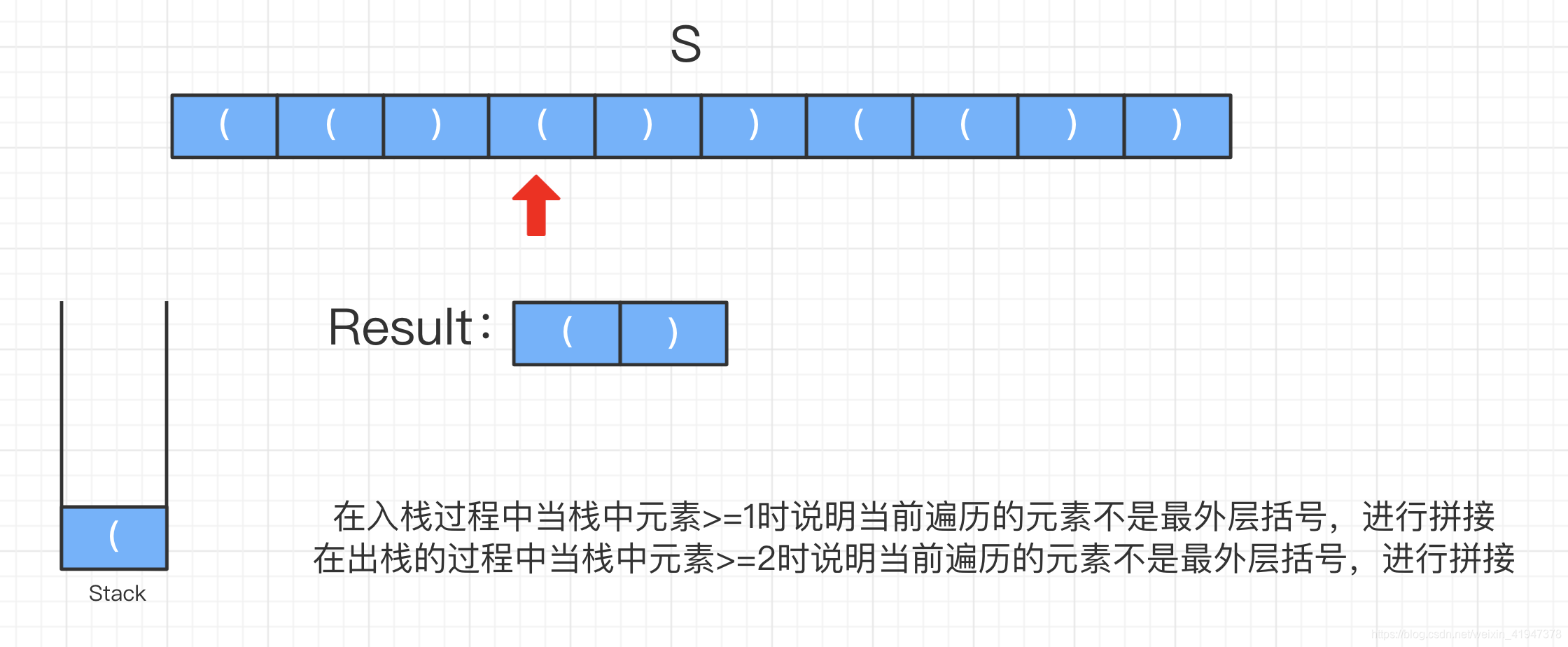
遍历到第二个元素，"("还是入栈，发现栈中元素数量 >= 1，说明此时遍历的元素是内层括号，进行拼接并入栈：

遍历到第三个元素，")“出栈，发现栈中元素数量 >=2，说明此时遍历到的”)"是内层括号，进行拼接并弹栈：

同理走到第6个元素的时候：

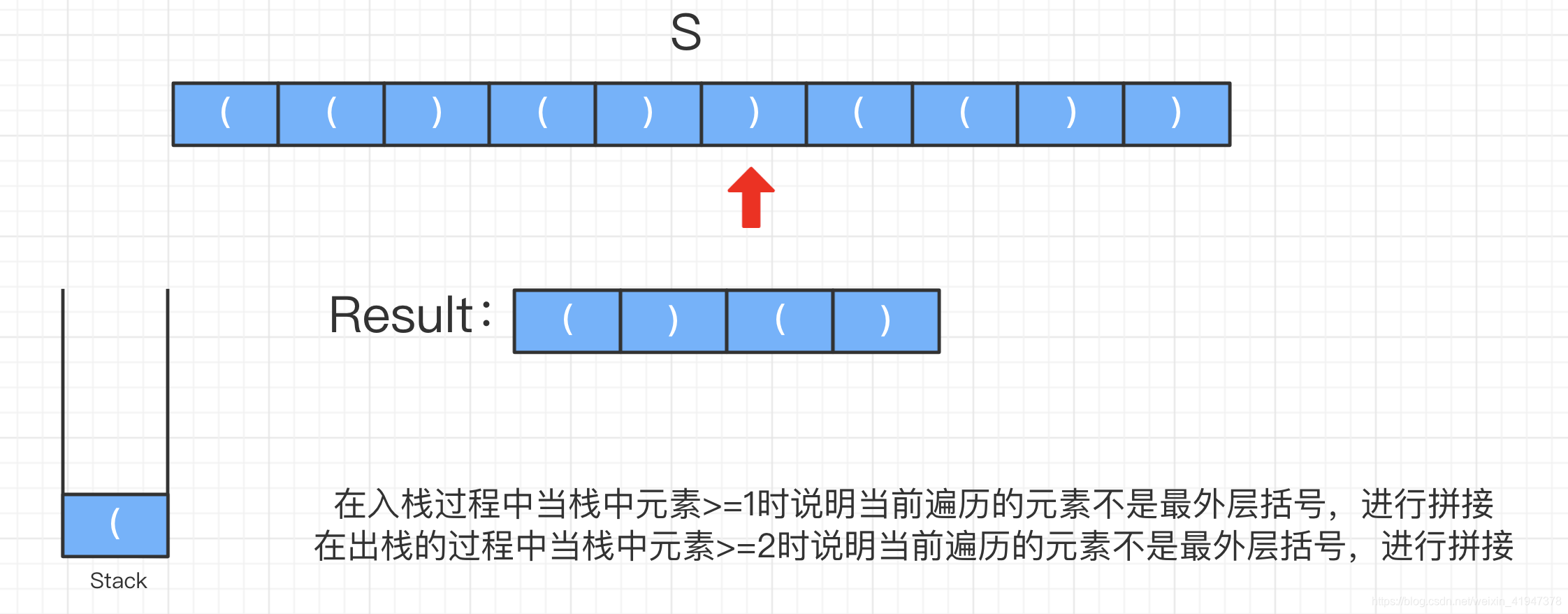
")“出栈，发现栈中元素数量 < 2，说明此时遍历到的”)"是最外层括号，需要删除，仅仅弹栈：

后面同理，最终可以拼接出一个去除最外层括号的字符串：

优化点：

• 因为只有一种类型的括号，并且栈的作用其实就是统计左右括号的差值，所以完全可以用一个变量代替，遇到"(" + 1，遇到")" - 1。

  这样虽然没有用到栈数据结构，但是思想是栈的思想，左右括号的差值本质上就是栈顶的指针，差值为0代表栈是空的

• 遇到")"，先进行出栈操作，再判断栈中元素个数是否>1
  遇到"("，先判断栈中元素个数是否>1，再进行入栈操作
  这样可以简化代码

class Solution {
    public String removeOuterParentheses(String S) {
        StringBuilder sb = new StringBuilder();
        // cnt记录左右括号的差值
        for (int i = 0, cnt = 0; i < S.length(); i++) {
            if (S.charAt(i) == ')') cnt--;
            if (cnt >= 1) sb.append(S.charAt(i));
            if (S.charAt(i) == '(') cnt++;
        }
        return sb.toString();
    }
}

3. LeetCode #1249 移除⽆效的括号

题目描述：
给你一个由 ‘(’、’)’ 和小写字母组成的字符串 s。

你需要从字符串中删除最少数目的 ‘(’ 或者 ‘)’ （可以删除任意位置的括号)，使得剩下的「括号字符串」有效。

请返回任意一个合法字符串。

有效「括号字符串」应当符合以下 任意一条 要求：

• 空字符串或只包含小写字母的字符串
• 可以被写作 AB（A 连接 B）的字符串，其中 A 和 B 都是有效「括号字符串」
• 可以被写作 (A) 的字符串，其中 A 是一个有效的「括号字符串」

解题思路：
可以被匹配的括号都是有效的，⽽其他的括号都需要被删除。

思路一：

• 从左往右遍历字符串，根据"("，把多的、不匹配的")"移除
• 再从右往左遍历字符串，根据")"，把多的、不匹配的"("移除

不用栈结构实现，因为只有一种类型括号字符，用变量，左括号+1，右括号-1即可

class Solution {
    public String minRemoveToMakeValid(String s) {
        char[] t = new char[s.length()];
        char[] ans = new char[s.length()];
        int tlen = 0;
        //从左到右遍历，移除无效的右括号
        //cnt记录左右括号的差值
        for (int i = 0, cnt = 0; i < s.length(); i++) {
            if (s.charAt(i) != ')') {
                if (s.charAt(i) == '(') cnt++;
                t[tlen++] = s.charAt(i);
            } else {
                if (cnt == 0) continue;
                cnt--;
                t[tlen++] = ')';
            }
        }
        //从右到左遍历，移除无效的左括号
        int ansHead = tlen;
        for (int i = tlen - 1, cnt = 0; i >= 0; i--) {
            if (t[i] != '(') {
                if (t[i] == ')') cnt++;
                ans[--ansHead] = t[i];
            } else {
                if (cnt == 0) continue;
                cnt--;
                ans[--ansHead] = '(';
            }
        }
        return new String(ans).trim();
    }
}

思路二：

• 确定所有需要删除字符的索引。
  使用栈当遇到 “(” 时，将其索引入栈，当遇到 “)” 时，若栈不为空且栈顶索引指向的元素是 “(” 时，则一起出栈，当扫描到字符串末尾时，最终剩下的索引都是需要删除的字符。
• 根据删除字符的索引创建一个新字符串。

遇到’)‘时，栈为空没有匹配的’(’，将其索引入栈：

继续走，索引走到3为’(’，直接入栈：

索引走到5时，由于栈顶元素为3对应的字符为’(’，刚好和’)'匹配，一起出栈：

索引走到8，栈顶没有匹配的’(’，入栈：

遍历完以后，最终栈中留下的索引都是要删除的字符，删除即可：

class Solution {
    public String minRemoveToMakeValid(String s) {
        LinkedList<Integer> stack = new LinkedList<>();
        for (int i = 0; i < s.length(); i++) {
            if (s.charAt(i) == '(') {
                stack.push(i);
            } else if (s.charAt(i) == ')') {
                if (!stack.isEmpty() && s.charAt(stack.peek()) == '(') {
                    stack.pop();
                } else {
                    stack.push(i);
                }
            }
        }
        StringBuilder sb = new StringBuilder(s);
        while (!stack.isEmpty()) {
            // 从后往前删，不会有问题
            sb.deleteCharAt(stack.pop());
        }
        return sb.toString();
    }
}

4. LeetCode #145 ⼆叉树的后序遍历

题目描述：
给定一个二叉树，返回它的 后序 遍历。

进阶: 递归算法很简单，你可以通过迭代算法完成吗？

解题思路：
递归方式⽐较简单，这⾥主要演示如何基于迭代实现。递归本质就是用了栈，Java用的是JVM中的方法栈，一个方法对应一个栈帧，方法的调用结束对应了栈帧的入栈和出栈。

• 如果用一个栈帧代表一个方法，每进入一个方法，我们就把该方法代表的栈帧压入栈中，每执行完退出一个方法，我们就把该方法代表的栈帧出栈，如果一个方法执行的过程中又嵌套调用了其他方法，进入了一个新的方法，我们就把新的方法对应的栈帧压栈，栈顶元素永远是正在执行的方法。
• 当嵌套调用的方法执行完出栈回到当前方法的时候，我们需要知道之前执行到哪了，已经执行过的代码不能在执行了，那么如何维护方法执行到哪了呢？

观察下图递归实现的后序遍历：

• 有一种简单的思路，我们可以将“遍历左⼦树”，“遍历右⼦树”和“访问根节点”三个操作分别⽤状态码表⽰：

  • 状态0代表遍历左子树
  • 状态1代表遍历右子树
  • 状态2代表访问根节点，并结束方法
  
  

  然后枚举状态转移过程，使⽤有限状态⾃动机（FSM, Finite State Machine）的模型来模拟递归过程。

• 另外栈帧需要维护哪些数据呢？首先肯定需要该方法的入参，即所需要处理的数据，其次就是用一个变量存储该方法的操作状态，维护该方法已经执行到哪了。实现角度来说可以专门封装一个“栈帧”的数据结构，根据题目要求需要三个属性维护节点、集合、状态，在配合一个栈模拟方法递归过程。嫌麻烦的话也可以用直接使用两个栈，一个存储节点一个存储状态。

以LeetCode样例数据为例：
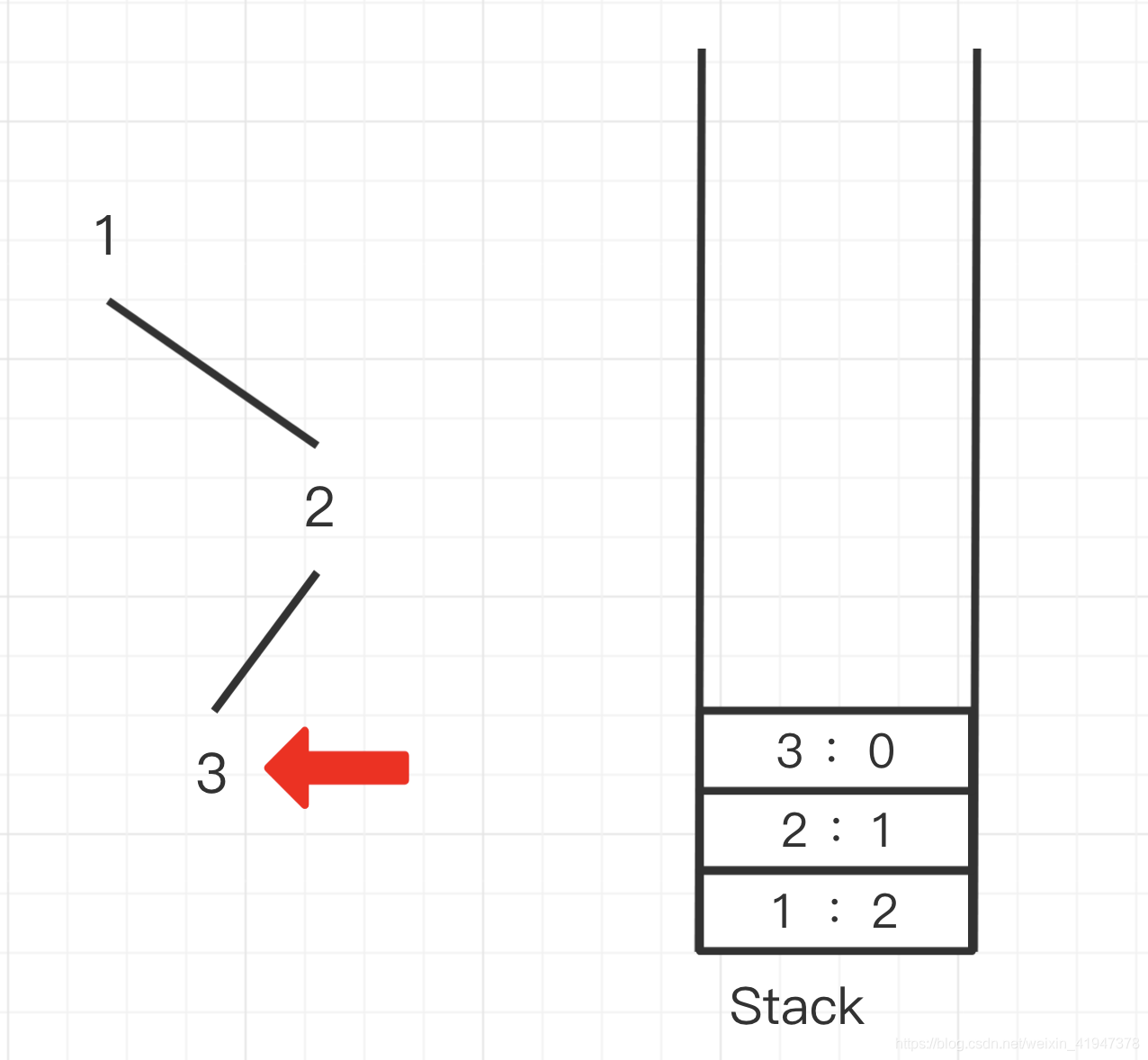
首先初始状态是将根节点放入栈中，同时节点的状态为0（图中栈中元素：左边是数据，右边是状态）：

开始处理栈顶元素，状态0代表遍历左子树，先将状态置为1，再执行遍历左子树操作，发现null不处理

再处理栈顶元素，状态1代表遍历右子树，先将状态置为2，再执行遍历右子树操作，发现不为null，将右子树新节点入栈，初始状态为0

此时栈顶是新的节点，状态0遍历左子树，先将状态置为1，再遍历左子树，左子树不为空，将新的节点入栈，初始状态为0：

继续处理栈顶元素，状态0，更新1后遍历左子树为空，不处理

继续处理栈顶元素，状态1，更新2后遍历右子树为空，不处理

继续遍历栈顶元素，状态2将节点值放入序列，并弹栈：

继续遍历栈顶元素，状态1，更新为2后遍历右子树为空不处理：

继续遍历栈顶元素，状态2将节点值放入序列，并弹栈：

继续遍历栈顶元素，状态2将节点值放入序列，并弹栈：

最终栈为空代表所有节点都处理完了，得到后序序列321

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        if (root == null) return result;
        LinkedList<TreeNode> dataStack = new LinkedList<>();
        // 0代表要处理左节点，1代表要处理右节点，2代表要处理根节点
        LinkedList<Integer> statusStack = new LinkedList<>();
        dataStack.push(root);
        statusStack.push(0);
        while (!dataStack.isEmpty()) {
            // 后序遍历，左右中
            Integer status = statusStack.pop();//状态要更新，所以这里直接弹栈
            TreeNode curNode = dataStack.peek();
            if (status == 0) {
                statusStack.push(1);//先更新状态，再进行操作
                // 处理左节点
                if (curNode.left != null) {
                    dataStack.push(curNode.left);
                    statusStack.push(0);
                }
            } else if (status == 1) {
                statusStack.push(2);
                // 处理右节点
                if (curNode.right != null) {
                    dataStack.push(curNode.right);
                    statusStack.push(0);
                }
            } else if (status == 2) {
                // 处理根节点
                result.add(curNode.val);
                dataStack.pop();
            }
        }
        return result;
    }
}