一、基础结构
栈是⼀种“先进后出”(FILO, First In Last Out)的数据结构。
以下是一种栈的逻辑结构:
- size代表栈的容量
- top指向栈顶元素
- data_type代表数据类型
如果用数组实现栈,我们可以把数组的索引位0代表栈底,上图是一个装有4个元素的栈
出栈的时候,top指针向下移动一位,减一即可:
入栈的时候top指针向上移动一位,加一,并将元素赋值到对应位置
二、栈思维
2.1 判断括号是否合法
我们以LeetCode20题,判断括号是否合法,作为引子:
题目描述
给定一个只包括 ‘(’,’)’,’{’,’}’,’[’,’]’ 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
- 1.左括号必须用相同类型的右括号闭合。
- 2.左括号必须以正确的顺序闭合。
思考:问题简化成只有一种括号,怎么做?
仔细观察,可以得到如下结论,只要同时满足以下两个条件即可:
- 1、在任意一个位置上,左靠号数量>=右括号数量
- 2、在最后一个位置上,左括号数量==右括号数量
因此代码实现中只需要记录左括号数量和右括号数量即可
public boolean isValid(String s) {
int left = 0;
int right = 0;
char[] arr = s.toCharArray();
for (char c : arr) {
switch (c) {
case '(': left++;break;
case ')': right++;break;
default: return false;
}
if (left < right) return false;
}
return left == right;
}
其实用一个变量即可,记录左右括号的差值即可:
public boolean isValid(String s) {
int difference = 0;
char[] arr = s.toCharArray();
for (char c : arr) {
switch (c) {
case '(': difference++;break;
case ')': difference--;break;
default: return false;
}
if (difference < 0) return false;
}
return difference == 0;
}
2.2 栈的思维方式
通过代码的实现,我们可以思考,引出新的思维方式:
-
1、+1 可以等价为【进】,-1可以等价为【出】+1代表多了一个“东西”,-1代表少了一个“东西”
-
2、一对 () 可以等价为一个完整的事件( 代表出现了一个问题,) 代表解决了这个问题
-
3、(()) 可以看做事件与事件之间的完全包含关系(( 代表想解决一个问题,但是要想解决这个大问题的时候要先解决一个小问题,当小问题解决了大问题就可以解决了,即 (())
基础的数据结构往往反应的是本质的思维方式 -
4、括号序列还可以代表函数执行funA 内调用 funB,funB 执行完了,调用 funC,funC执行完了,funA才能执行完

-
5、由括号的等价变换,得到了一个新的数据结构,栈
所以:
为什么栈可以处理表达式求值
为什么栈可以处理递归程序(因为程序之间的调用就是完全包含关系)
为什么栈可以处理括号匹配
为什么栈可以处理二叉树遍历
…
比如:
二叉树,顶节点看成集合,下面两个节点看成子集,就可以看成是(()())
函数调用类似:
二叉树遍历:
遍历1号,遍历2号,遍历2号结束,遍历3号,遍历3号结束,遍历1号结束
因此一个括号序列,有可能是一个二叉树、有可能是一个函数调用关系,也可能是一个表达式的计算过程(经常看到所谓的语法树就是这个原理)
最后重要的事说三遍:
- 栈可以处理具有完全包含关系的问题!
- 栈可以处理具有完全包含关系的问题!
- 栈可以处理具有完全包含关系的问题!
三、经典的栈实现方法
3.1 利用现成的Java类库实现的简单栈:
public class MyStack {
LinkedList<Integer> linkedList = new LinkedList<>();
void push(int value) {
linkedList.addLast(value);
}
void pop() {
if (empty()) return;
linkedList.removeLast();
}
boolean empty() {
return linkedList.size() == 0;
}
int size() {
return linkedList.size();
}
void output() {
System.out.println("=====");
for (int i = size() - 1; i >= 0; i--) {
System.out.println(" " + linkedList.get(i));
}
System.out.println("=====");
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
MyStack myStack = new MyStack();
String operate = null;
while ((operate = sc.nextLine()) != null) {
switch (operate) {
case "push":
myStack.push(sc.nextInt());
break;
case "pop":
myStack.pop();
break;
case "size":
System.out.println(myStack.size());
break;
case "output":
myStack.output();
break;
}
}
}
}
3.2 利用数组+指针实现
public class MyStack2 {
int[] array;
int top;
public MyStack2(int size) {
array = new int[size];
//如果栈顶指针为空的话通常指向-1位置
top = -1;
}
void push(int value) {
if (full()) return;
array[++top] = value;
}
void pop() {
if (empty()) return;
top--;
}
boolean full() {
return top == array.length - 1;
}
boolean empty() {
return top == -1;
}
int size() {
return top + 1;
}
void output() {
System.out.println("=====");
for (int i = size() - 1; i >= 0; i--) {
System.out.println(" " + array[i]);
}
System.out.println("=====");
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
MyStack2 myStack = new MyStack2(10);
String operate = null;
while ((operate = sc.nextLine()) != null) {
switch (operate) {
case "push":
myStack.push(sc.nextInt());
break;
case "pop":
myStack.pop();
break;
case "size":
System.out.println(myStack.size());
break;
case "output":
myStack.output();
break;
}
}
}
}
四、栈的典型应用场景
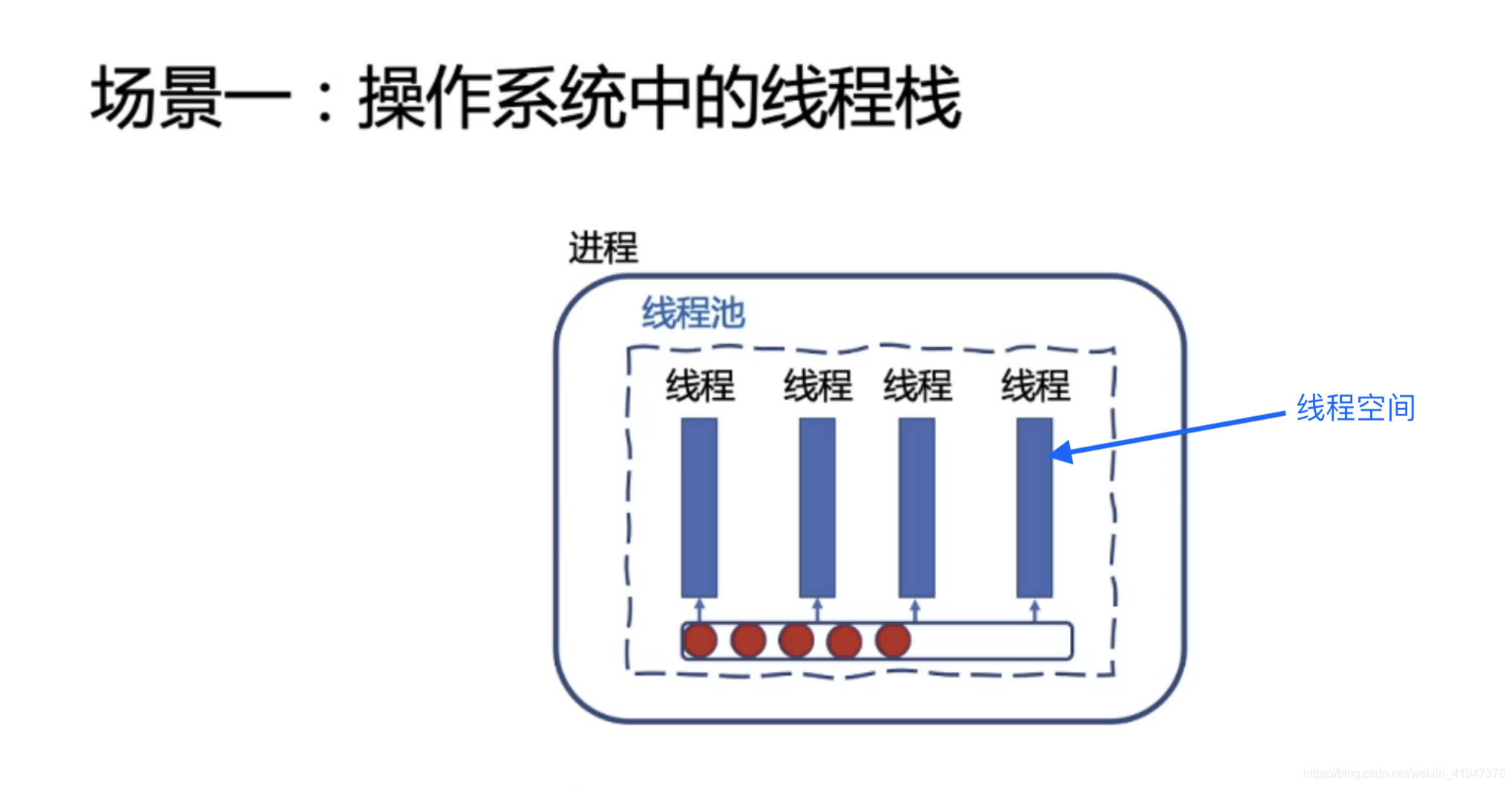
4.1 操作系统中的线程栈
线程空间本质上就是个栈,因此也叫做线程栈
-
程序中申请的局部变量都是存储在线程空间中,即栈空间中的
-
栈大小就是线程栈的大小,当申请一个线程的时候,线程所占的线程空间大小默认就是8M

-
爆栈:当向线程栈中压入的局部变量的总大小超过线程栈大小的时候,就会爆栈
8M = 800万个字节,一个整形变量占4个字节,如果在线程栈中压入200W个整形就一定会爆栈
-
栈溢出:函数递归层数超过指定的数
-
多线程编程:每申请一个线程要占用8M空间,如果申请1000个线程光线程栈就要占8G
4.2 表达式求值
平常写的递归函数实际上用的就是系统栈,而栈实现只不过是用我们手动写的栈,本质都是在用栈
表达式树,通常以运算符作为根节点,以相关的操作数作为相应的子节点:
上图可以认为是一个乘法表达式,为什么说这是个乘法表达式:因为乘号是整个表达式中最后一个被计算的运算符,即优先级最低的运算符
由此可以推导出一种递归式的表达式求解的方法,假设有一个递归函数calc,用来算大的表达式的值
-
第一步先找到整个表达式中优先级最低的运算符位置在哪
我们给+ -基础优先级定为1,* /的基础优先级为2,在括号里面的运算符优先级我们额外增加100,通过这种规则可以确定每一个运算符的优先级,找到优先级最低的位置

如果是更复杂一点的

-
然后从优先级最低的位置把原来的表达式拆成两部分,在分别递归调用calc函数对这两部分表达式进行求解

-
最后将两个表达式的解根据当前运算符完成计算
public class MyCalculator {
public static void main(String[] args) {
String expression = "(1+2) + 4 * 2 + 10/2";
//calc方法,第一个参数是表达式,第二、三个参数是表达式的范围
int calc = calc(expression, 0, expression.length() - 1);
System.out.println(calc);
}
/**
* @param expression 算数表达式
* @param start 表达式有效范围的起始位置
* @param end 表达式有效范围的结束位置
*/
private static int calc(String expression, int start, int end) {
int lowest = -1;// 指向优先级最低的运算符的位置
int pri = 10000 - 1;// 上一个符号的优先级,初始给个较大值减少代码判断
int temp = 0;// 由括号增加的优先级
//遍历运算符找到优先级最低的
for (int i = start; i <= end; i++) {
int cur = 10000;// 当前符号优先级,初始给个较大值减少代码判断
char c = expression.charAt(i);
switch (c) {
case ' ':
continue;
case '+':
case '-':
cur = temp + 1;
break;
case '*':
case '/':
cur = temp + 2;
break;
case '(':
temp += 100;
break;
case ')':
temp -= 100;
break;
}
if (cur < pri) {
pri = cur;
lowest = i;
}
}
// 当op=-1,说明当前表达式没有运算符,转成数字返回
if (lowest == -1) {
int num = 0;
for (int i = start; i <= end; i++) {
// 排除 ( 和 )
char c = expression.charAt(i);
if (c < '0' || c > '9') continue;
num = (num * 10) + c - '0';
}
return num;
}
// 否则根据最低运算符的位置拆成两个表达式递归调用
// 再将得到的两个返回值进行计算
int left = calc(expression, start, lowest - 1);
int right = calc(expression, lowest + 1, end);
// 根据当前算数运算符进行计算
int result = 0;
char c = expression.charAt(lowest);
switch (c) {
case '+':
result = left + right;
break;
case '-':
result = left - right;
break;
case '*':
result = left * right;
break;
case '/':
result = left / right;
break;
}
return result;
}
}



































 453
453

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










