PCA 主成分分析理解(一）

  该系列博客都是对记录对学习花书（深度学习）的知识，仅供自己复习总结，截图的来源也为花书
  主成分分析(principal components analysis, PCA)是一个简单的机器学习算法，PCA算法假设在 Rn 空间中我们有 m 个点 {x(1), . . . , x(m)}，我们希望对这些点进行有损压缩，但是损失的精度尽可能小，我们希望能找到一个编码函数，将n维的xi编码成l维，l<<n.根据输入返回编码，f(x) = c;我们也希望找到一 个解码函数，给定编码重构输入，x ≈ g(f(x))
  PCA由我们选择的编码函数而定，直接决定选择何种编码函数可能无从下手，但是解码的结果与x直接相关，可以利用x来判断解码的优劣
  利用矩阵乘法将编码映射回n维空间，即 g(c) = Dc，D是定义解码的矩阵。
  (1).首先我们需要明确如何根据每 一个输入 x 得到一个最优编码 c∗,一种方法是最小化原始向量x和重构向量g(c∗)之间的距离：
  ![在这里插入图片描述](https://img-blog.csdnimg.cn/20190818213519214.png)
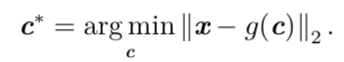
  c代表编码函数的值，找到使距离最小的编码即最优编码
  我们可以用平方 L2 范数替代 L2 范数，因为两者在相同的值 c 上取得最小值。 这是因为 L2 范数是非负的，并且平方运算在非负值上是单调递增的。

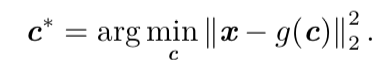
可以简化成：

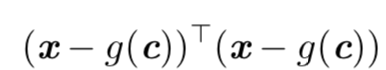
展开提取式子中与c有关的项，得：

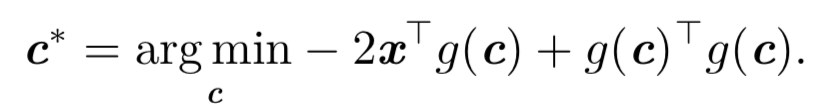
代入g©=Dc得：

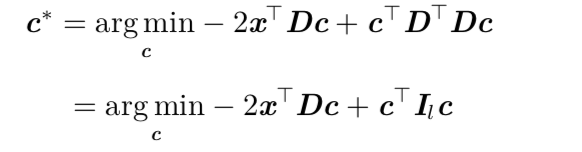
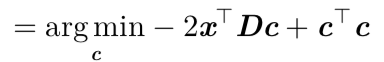
通过对上式求解（具体过程参考花书）最后表达式为：

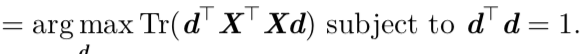
这个优化问题可以通过特征分解来求解。具体来讲，最优的 d 是 X⊤X 最大特 征值对应的特征向量。