PCA 主成分分析理解(二）

  该系列博客都是对记录对学习花书（深度学习）的知识，仅供自己复习总结，截图的来源也为花书
  在上篇博客中将PCA理解为一种压缩数据的方法，保留尽可能多原始数据的一种降维方法，这篇博客中将PCA理解为一种学习数据表示的无监督方法。
  PCA学习一种比原始输入更低维的表示，学习了一种元素之间没有相关性的表示。研究PCA是如何对原始数据x去相关的。
  ![在这里插入图片描述](https://img-blog.csdnimg.cn/20190825195725620.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80MTk0NjY2MQ==,size_16,color_FFFFFF,t_70)
  如果Z的协方差矩阵是对角矩阵，说明各变量之间没有相关性。
  由上篇博客可知，设计X的主成分由X⊤ X 的特征向量给定，所以我们有
  ![在这里插入图片描述](https://img-blog.csdnimg.cn/20190825200127352.png)
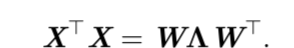
  这里从另一个角度，如果通过SVD分解，有：
  ![在这里插入图片描述](https://img-blog.csdnimg.cn/20190825200718967.png)
  ![在这里插入图片描述](https://img-blog.csdnimg.cn/20190825200824538.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80MTk0NjY2MQ==,size_16,color_FFFFFF,t_70)
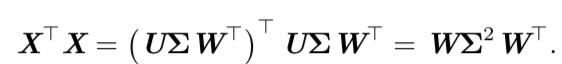
  以上分析表明，通过W将X变换为Z之后，Z中的各个变量是不相关的。