二叉堆的构建以及上滤与下滤

实现优先队列我们可以有以下几种方式：
1.链表实现
2.二叉查找树
3.堆

其中，二叉堆在优先队列的使用非常普遍

二叉堆的两个性质：

• 1.结构性

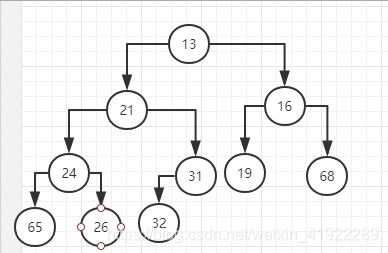
  • 堆实际上是一棵完全二叉树，底层元素从左到右填入，所以堆的高度为logN，因为完全二叉树的规律性，堆其实可以看作是一个数组，在这个数组中，父节点位于 i /2 位置，则左子节点则在 2i位置，右子节点在 2i + 1上

• 2.堆序性

  • 让堆操作快速执行的性质是堆序性，最小元位于根上，在一个堆中，对于每一个节点X，X的父亲小于或者等于X，根节点除外

堆的每一次操作都可能会破坏这两个性质中的其中一个，只有当所有性质都被满足时才能停止

在构建堆之前，先了解堆的两个很重要的操作，上滤和下滤，这是保持堆性质的两个重要操作

上滤

	
	/**
	 * 向堆中插入元素  ---- 上滤 ---- O(logN)
	 * @param x
	 */
	private void insert(AnyType x) {
		
		//判断当前堆（数组）是否已满，满则扩容，防止数组越界
		if(currentSize == array.length -1)
			enlargeArray(array.length * 2 + 1);
		
		//将要插入的元素放在最后一个叶子节点，即数组最后一个元素的位置
		int hole = ++currentSize;
		
		//父节点 ：hole / 2 
		//左子节点：2*hole
		//右子节点：2*hole+1
		//x和父节点比较，比父节点大则上滤，原父节点下滤
		for(array[0] = x ;x.compareTo(array[hole/2]) < 0 ; hole/=2) {
			array[hole] = array[hole / 2];
		}
		//最后再将要插入的值赋值过去符合的节点处
		array[hole] = x;
	}
	

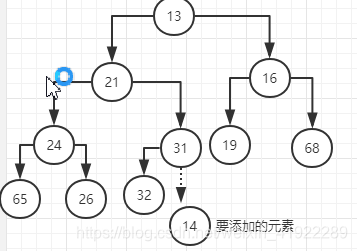
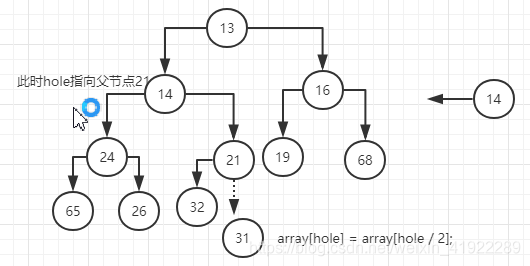
此时，array[hole/2]是他的父节点 — 31,14比31小，则此时

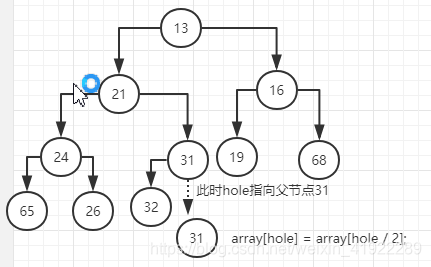
在进行插入

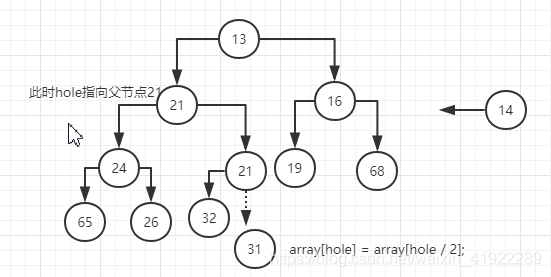
此时，要插入的14小于根节点13，此时已经符合堆序性，不需要在进行交换，这时只要将要插入的14赋值到当前hole指针指向的节点

下滤思想跟上边其实很相似，流程图就不写了，java数据结构与算法分析书里很详细
下滤

	/**
	 * 下滤 ---- O(logN)
	 * @param hole
	 */
	private void percolateDown(int hole) {
		
		int child;
		AnyType tmp = array[hole];
		
		for(; hole * 2 <= currentSize;hole = child) {
				
			child = hole * 2;
			//左子节点>右子节点
			if(array[child].compareTo(array[child+1]) < 0)
				//转向右子节点
				child++;
			//左子节点小于父节点
		    if(array[child].compareTo(tmp) < 0)
				//左子节点称为新的父节点
				array[hole] = array[child];
			else 
				break;
			
		}
		//完成交换
		array[hole] = tmp;
		
	}

构建堆

	/**
	 * 构建堆
	 */
	public BinaryHeap() {
		for(int i = currentSize/2;i>0;i--) {
			percolateDown(i);
		}
	}