文章目录
Semi-supervised Learning
Introduction
Supervised Learning
训练数据是一个function的输入和输出构成的pair

Semi-supervised Learning

训练数据有两部分:
- 在label data上一个function的输入和输出构成的pair
- 在unlabel data上,只有function的输入,没有输出
期待unlabel的data数量远大于label的data数量
半监督学习氛围两种:
- Transductive learning:unlabel data就是测试集,使用他的feature(如果使用测试集的label就是作弊)
- Inductive learning:unlabel data不是测试集,无法事先根据测试集做任何事情
Why semi-supervised learning?
- 收集数据很容易,但是收集有标签的数据很难。
- 对人类来说,我们在我们的生活中也是做半监督学习的。

Why semi-supervised learning?
有一部分labeled的data,还有一部分unlabeled的data

unlabeled data的分布可能会告诉我们一些信息,eg切割的边界线,但是半监督学习使用unlabelled data 的方式往往伴随着一些假设,半监督学习是否有用,往往取决于假设是否符合实际,是否精确。
所以半监督学习未必一直有用,他取决于所做的假设是否合适。

Outline
Semi-supervised Learning for Generative Model
Supervised Generative Model

Semi-supervised Generative Model

Supervised Generative Model 流程
Step1:计算每笔unlabelled data的后验概率
假设是二元分类问题的话,先初始化一组参数,初始化 P ( C 1 ) P(C_1) P(C1)和 P ( C 2 ) P(C_2) P(C2), μ 1 \mu^1 μ1, μ 2 \mu^2 μ2, ∑ \sum ∑,初始化的值可以random产生也可以又labelled data得来。
把 P ( C 1 ) P(C_1) P(C1)和 P ( C 2 ) P(C_2) P(C2), μ 1 \mu^1 μ1, μ 2 \mu^2 μ2, ∑ \sum ∑这些参数统称为: θ \theta θ
根据已有的 θ \theta θ,可以估算每笔unlabelled data属于class1 的几率,几率取决于model的 θ \theta θ。
Step2:更新模型
更新模型的公式很直觉。
原来没有考虑unlabelled data的时候,N可能是所有的example,N1是标记为C1的example数目,则不考虑unlabelled data时候, P ( C 1 ) = N 1 / N P(C_1)=N_1/N P(C1)=N1/N
现在考虑unlabelled data的公式:
P
(
C
1
)
=
N
1
+
∑
x
u
P
(
C
1
∣
x
u
)
N
P(C_1)=\frac{N_1+\sum_{x^u}{P(C_1|x^u)}}{N}
P(C1)=NN1+∑xuP(C1∣xu)
在更新之后,有了新的model,返回第一步;
有了新的model后,几率
P
θ
(
C
1
∣
x
u
)
P_\theta(C_1|x^u)
Pθ(C1∣xu)又会改变,就会进行第二步,model又不一样了,以此类推。。。
理论上这个方法在最后是收敛的,但是初始值会影响收敛的结果。

Why?
- Maximum likelyhood with labelled data
原来只有labelled data的时候,我们要做的事情是要最大化一个likely hood或者log likely hood,每笔训练数据的likely hood是可以计算的(如图),求和后是total likely hood
- Maximum likelyhood with labelled + unlabelled data
公式纠正:
l o g L ( θ ) = ∑ x r l o g P θ ( x r , y ^ r ) + ∑ x u l o g P θ ( x u ) logL(\theta)=\sum_{x^r}logP_\theta(x^r,\hat{y}^r)+\sum_{x^u}logP_\theta(x^u) logL(θ)=∑xrlogPθ(xr,y^r)+∑xulogPθ(xu)
labelled data和前面公式一样,但是unlabelled data需要估测他的概率,一笔unlabelled data不知道是从C1还是C2来,所以,
一笔unlabelled data出现的概率 = C1的概率和C1类别产生这笔unlabelled data的概率之积 + C2的概率和C2类别产生这笔unlabelled data的概率之积,求和后,即为这笔unlabelled data出现的概率。
接下来,就是最大化该式——
l
o
g
L
(
θ
)
logL(\theta)
logL(θ)。

但是不幸的是,解开这个式子只能重复地去解这个式子(即,前面幻灯片里的step1和step2不断重复),不断地增大
l
o
g
L
(
θ
)
logL(\theta)
logL(θ),最后会收敛到一个locla minimum局部最优的地方。
Semi-supervised Learning Low-density Separation
比较通常的一个方法,基于的假设为Low-density Separation,即“非黑即白”,在labelled和unlabelled data之间有很明显的分界线。
给出如图的data,边界线可能有如图两条,但是要考虑unlabelled data的话,左边的是好的,右边的是不好的,
在两个class的交界处的density是最低的,这种边界才是比较合理的。

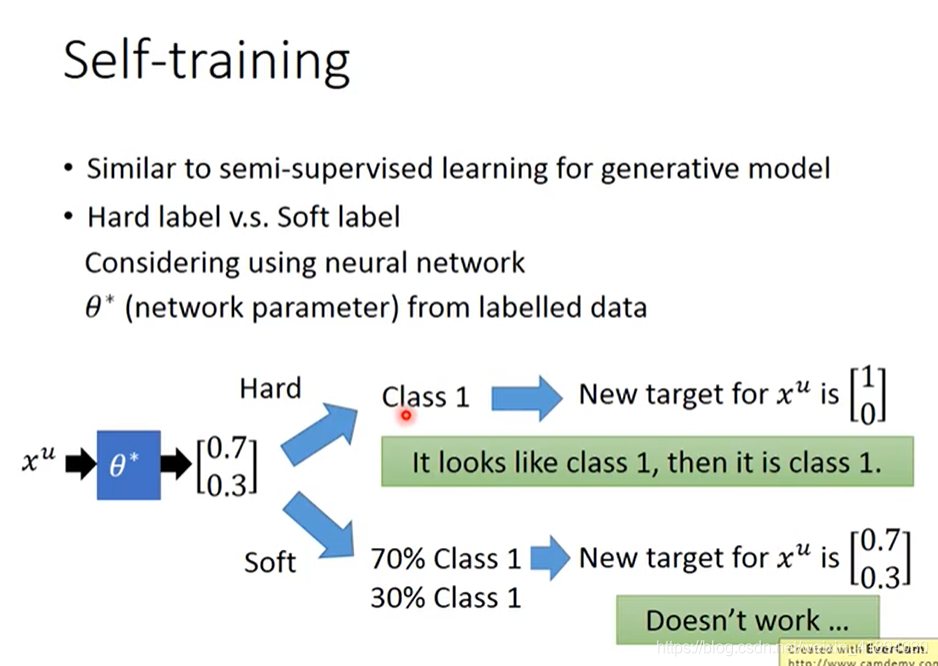
Self-training
最简单,最具代表性,太直觉了。
有labelled和unlabelled data:
- 从labelled data中训练一个模型 f ∗ f^* f∗,
- 然后用这个模型去label你的unlabelled data,即输入unlabelled data,查看输出,叫做Pseudo-label。
- 从unlabelled data set中拿出一些放到labelled data set中,具体如何选择要加进去是一个开放问题,需要自己想办法解决。
- 有了更多的data之后,labelled data从unlabelled data中得到了更多的data,就返回第一步,再去训练 f ∗ f^* f∗,十分直觉

这个方法可以用在回归问题上吗?
回归问题是要输出一个实数,把一部分data加入labelled data后,再训练,并不会影响 f ∗ f^* f∗,所以regression不可以使用这个方法。
对比
- 与Semi-supervised Learning for Generative Model很相似
- 在做Self-training的时候用的是Hard label,在做Semi-supervised Learning for Generative Model的时候,用的是soft label。
- 在做Self-training的时候会强制指定一笔训练数据属于某一个class,而在做Semi-supervised Learning for Generative Model的时候,根据后验概率,一部分属于class1,一部分属于class2.
- 在使用神经网络的时候,一定要用hard的label,soft label没有用!(hard label的假设更加强烈,而soft的相当于没有,原本的参数就可以达到target了)
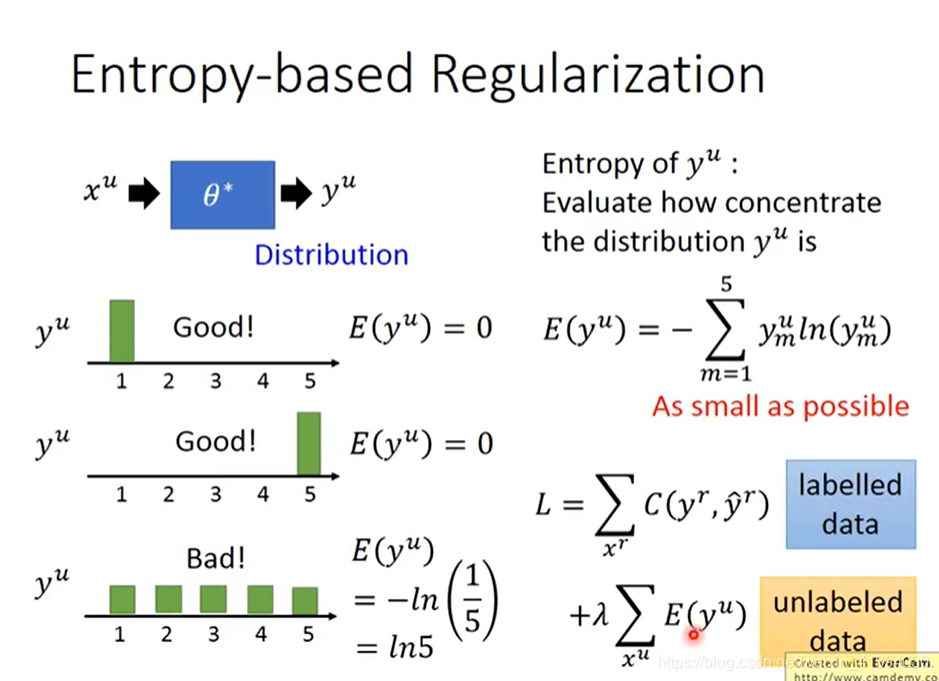
Entropy-based Regularization
可能前面的hard label的方法太武断,可以用Entropy-based Regularization
output是一个分布,但是分布也要集中,因为“世界”是非黑即白的,过于平均不符合low-density separation的假设。
那么要如何用一个数值来评价一个分布是好还是不好,集中还是不集中呢??
使用Entropy来评价。分布比较集中的Entropy比较小。
根据前面的内容,重新设计Loss function
- labelled data部分, y r y^r yr和 y ^ r \hat{y}^r y^r之间越近越好,可以使用cross entropy来评价距离。
- unlabelled data部分,使用每笔data的output的分布的entropy,希望越小越好
- 还可以添加一个weight参数
λ
\lambda
λ来代表,其所占的权重。
训练依旧使用梯度下降来最小化L,类似于Regularization(在原来的loss function后,加一个参数的L1或L2,来防止过拟合),现在这个很类似,现在加上一个根据unlabelled data来得到的entropy,来防止过拟合,称作Entropy-based Regularization。
Outlook: Semi-supervised SVM
目标:
找一个可以提供最大margin,最小error的分界线。
过程:
- 穷举unlabelled data的所有可能的标签
- 对每种可能的标签都做一次SVM

Semi-supervised Learning Smoothness Assumption
思想:近朱者赤近墨者黑

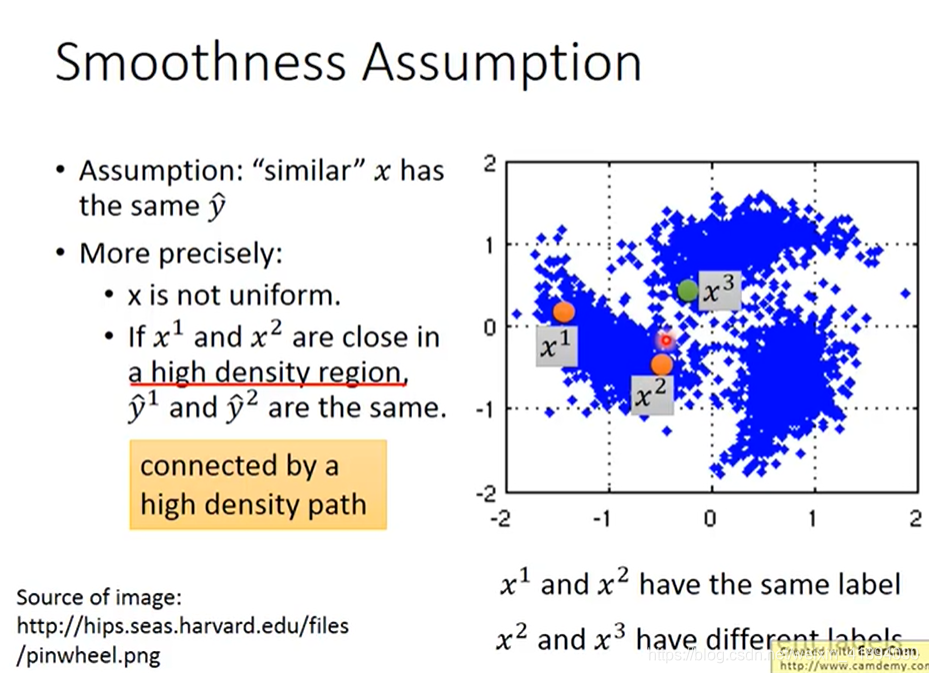
Smothness Assumption
假设: 如果x是像的,那么他们的label y也会相似。
但是这样假设是不精确的
更精确的假设:
- x的分布是不平均的,某些地方很集中,某些地方很分散
- x1和x2在一个高密度的区域的话,那么x1和x2很接近的时候,他们的label才会很像。x1和x2之间有一条高密度的路径。
假设有3笔data,分布如图,貌似x2和x3离得近,如果考虑那个比较粗糙的假设,则他们比较像。
但是在更精确的假设中,要通过一个高密度的区域来像,即x1和x2中间有一个高密度的区域,相连是通过一条高密度的路径。
中间的2貌似和3更相似
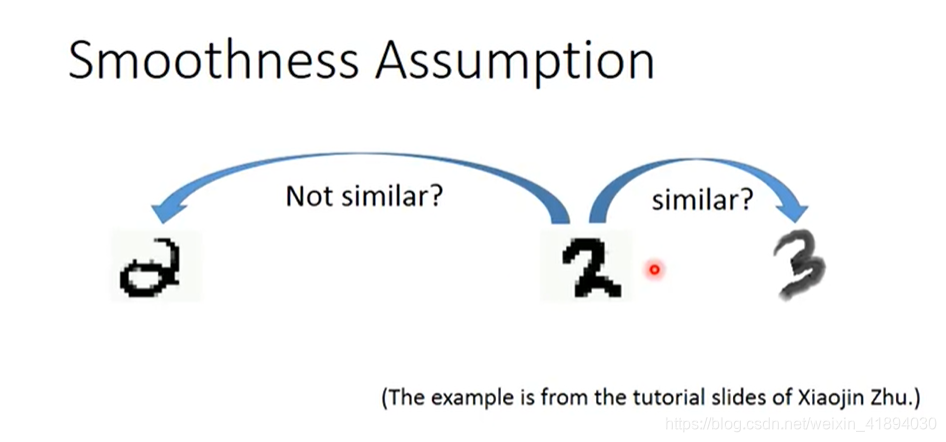
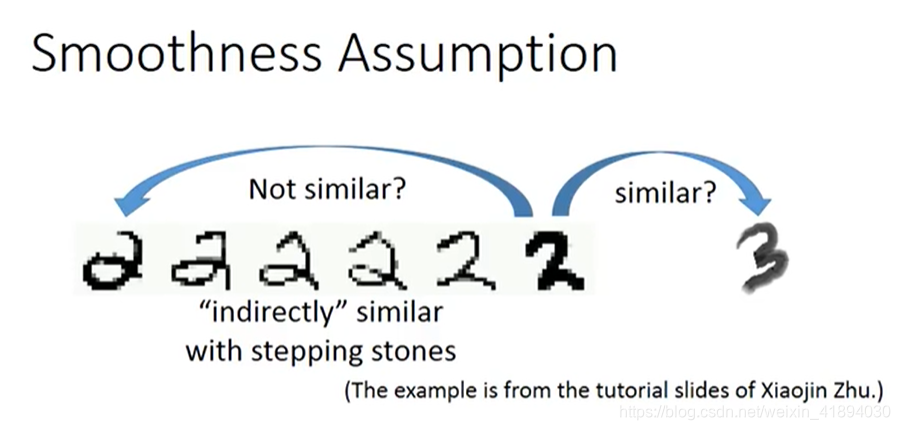
但是第一个2可以通过一系列连续的形态转换为第二个2
所以我们要用Smoothness Assumption
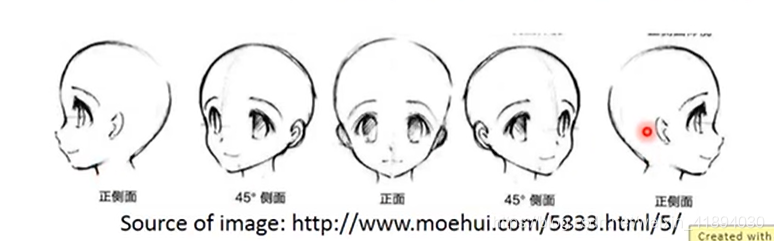
人脸同理。左1到右1有很多过度形态。
在文件分类上也有用,天文学和旅游文章分类。

数据足够多的时候

如何实现Smoothness Assumption
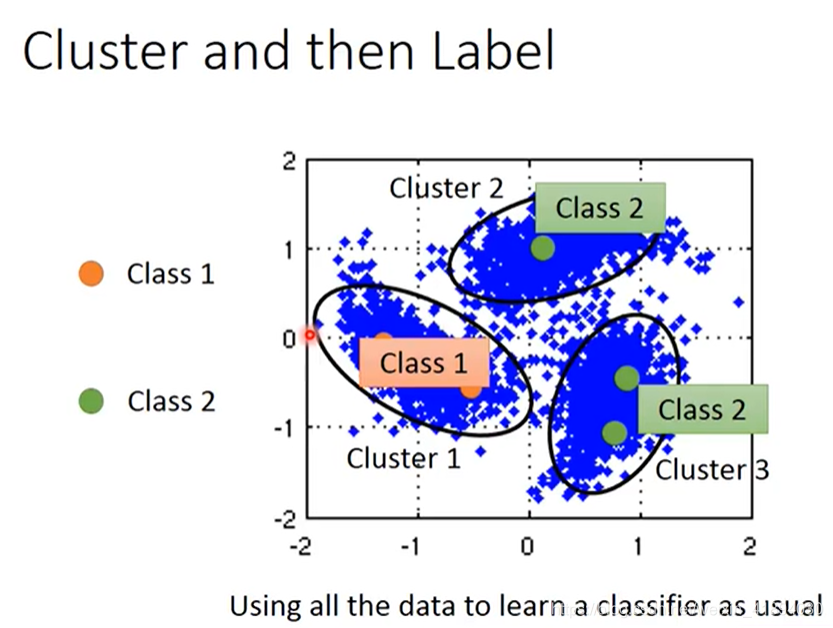
Cluster and then Label
这是最简单的方法。
橙色是class1,绿色是class2,蓝色是unlabelled data。
把所有数据先聚类,分出三个cluster,观察cluster1中,class1的label data最多,所以把cluster1中的所有data都归于class1,同理,cluster2和cluster3都归于class2。
Graph-based Approach
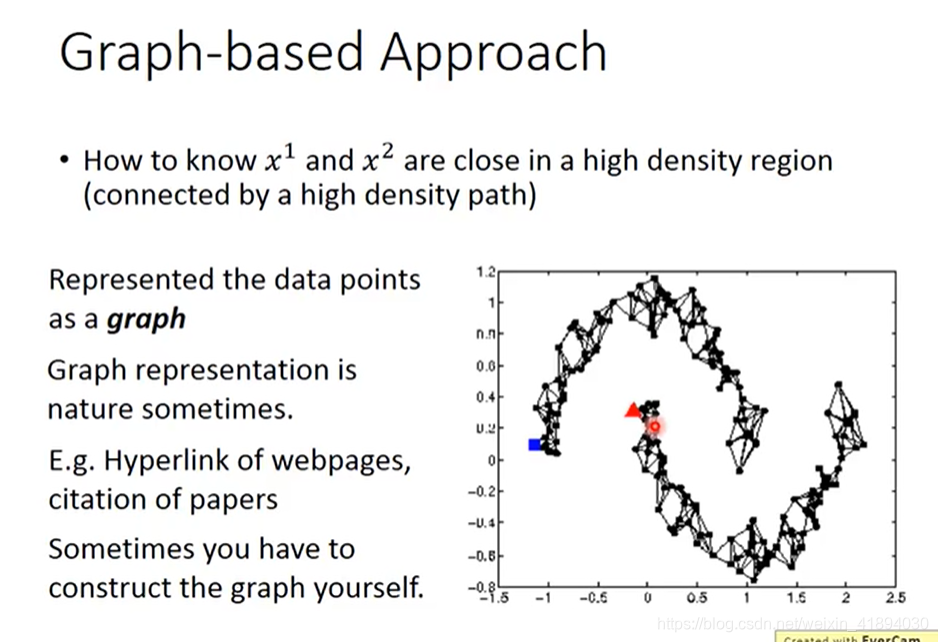
引入Graph structure,使用图结构来表达conneced by a high density path。
把所有的数据点都建成一个图,每笔data point x都是图上一个点,想要计算他们的相似度,要把图的边建立出来。
如果现在有两个点之间有边,可以走的到,说明是同一个class,否则,哪怕距离很近,也走不到,不是同一类。
如何建图呢?
- 有时建图是很自然的。eg:网页超链接,论文的引用关系。
- 有时需要自己想办法自己建图
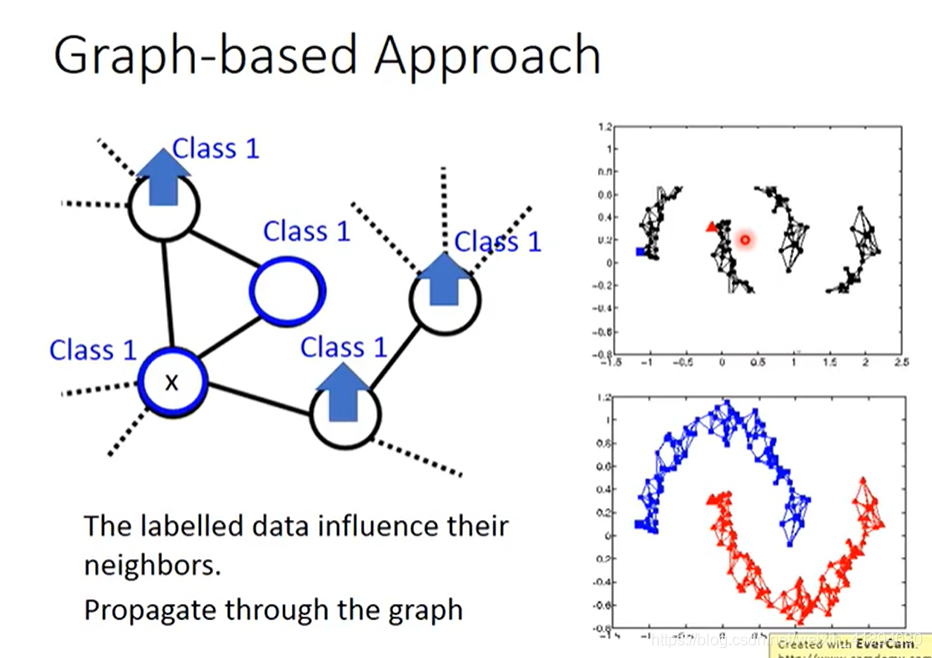
Graph-based Approach - Graph Construction
- 定义两个点之间计算相似度的方法
- 添加边
- 边的权重与点和点之间的距离成正比

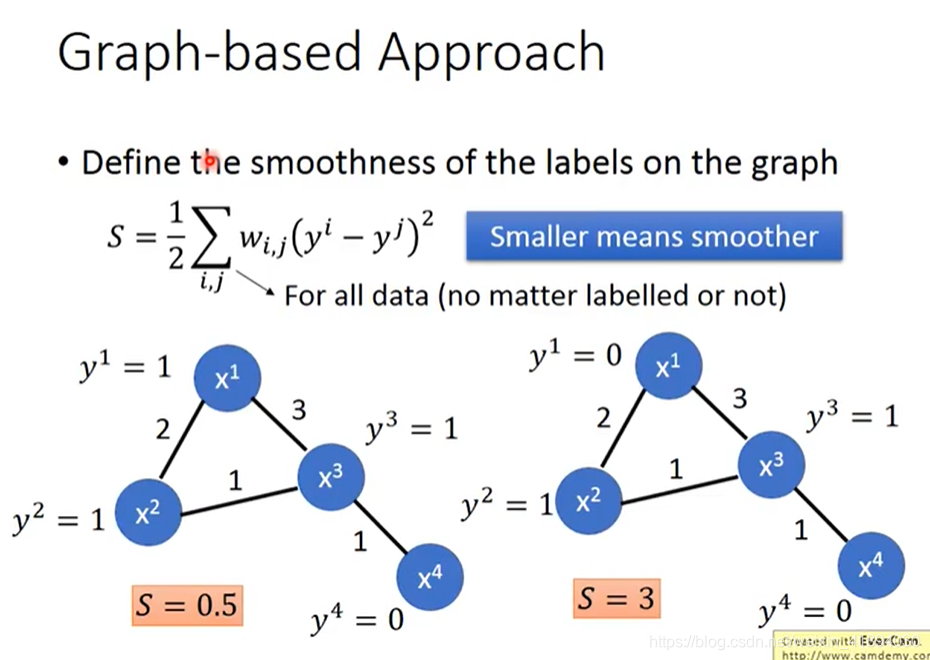
如何定量地描述这个图上label的光滑度呢?
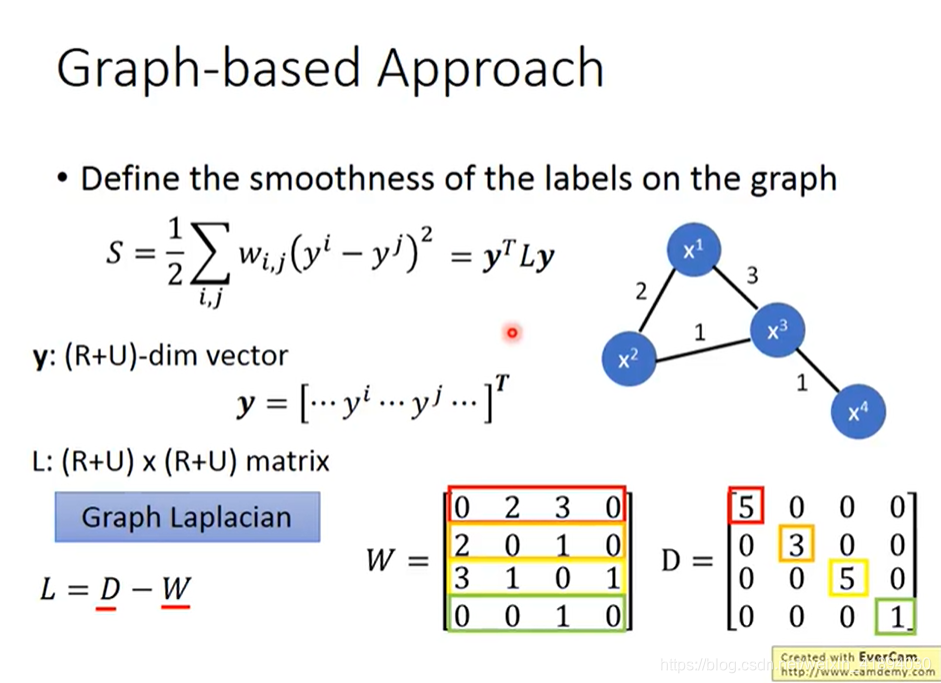
训练也可以运用梯度下降
smoothness可以放在任何地方

Semi-supervised Learning Bette Representation
思想:去芜存菁,化繁为简









 本文深入探讨半监督学习的概念,包括其在数据稀缺场景下的优势,以及如何利用未标记数据提升模型性能。涵盖生成模型、低密度分离、自训练等方法,并讨论了平滑假设的应用。
本文深入探讨半监督学习的概念,包括其在数据稀缺场景下的优势,以及如何利用未标记数据提升模型性能。涵盖生成模型、低密度分离、自训练等方法,并讨论了平滑假设的应用。
















 1174
1174

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








