解决回溯法 - 回溯到底是个什么东西(含有大量经典例题加详细分析）

最新推荐文章于 2023-02-08 14:55:23 发布

Taylor......

最新推荐文章于 2023-02-08 14:55:23 发布

阅读量3.9k

点赞数 3

分类专栏：数据结构

数据结构专栏收录该内容

2 篇文章

订阅专栏

文章目录

转自： https://blog.youkuaiyun.com/qq_39382769/article/details/80796100

一、用最通俗的话解释回溯思想：

回溯思想其实也可以叫做试探思想

有时候我们需要得到问题的解，先从其中某一种情况进行试探，在试探的过程中，一旦发现原来的选择是错

误的，那么就退回一步重新选择，然后继续向前试探，反复这样的过程直到求解出问题的解（试探思想充斥

在生活的各个地方）

其实一句话：回溯就是带优化的穷举，归根结底，还是一种有暴力的影子在里面，只不过带剪枝而已

牢记6个字：带优化的穷举，记住了回溯想不懂都难

看看最正统的回溯思想概念：
在这里插入图片描述
很官方很学术的一种解释，但无疑是挑不出毛病的，但是第一次看的话，比较难懂，需要注意的是采用回溯

法的时候我们是边搜索边构造状态空间树，想想，如果我们一开始就是把状态空间树全部构造出来，然后再

搜索的话，会消耗很大的空间，且在Cutting的时候大部分的枝叶都剪掉了，全部构造出来完全没有必要嘛

回溯与分支限界很类似，回溯是DFS+Cutting，而分支限界是BFS+Cutting
如果要用回溯求解问题的所有解，则要回溯到根，且根结点的所有子树都已经被搜索才结束
如果只要求解任一解，则只要搜索到问题的一个解就可结束

二、经典例子

1.经典样例1：（01背包问题的回溯解法）

01背包问题真的是一个老生常谈的问题，分治，dp，贪心，回溯到处都可以见到它，用分治的话效率低

下，用贪心的话解不出来，但是可以求出近似最优当作参考

第一步：画解空间树

                                                 A

                                         1 /        0\

                                       B                B

                                  1 /   0\       1/     0\

                                 C         C      C        C

A,B,C三个物品，1代表选择，0代表不选

这就是所谓的解空间树，搜索到叶子结点，问题也就结束了

第二步：设计Cutting函数

有时候做题，超时还是不超时，完全就是看你的Cutting函数设计的怎么样，回溯的重点不在于解空间树，

而是在于Cutting函数的设计

CUtting函数有两个分类：

第一个：约束函数：即不满足约束条件，比如01背包问题中的背包装不下了

第二个：限界函数：即这条路走了，没有走另外一条路好，少年，回头吧，走另外一条路

下面开始我们Cutting函数的设计

最简单的一个：背包装不下的时候肯定不能再装该物品

即：要求已经装了的物品重量加上该物品的重量<=背包容量

即装得下就装，装不下就剪

这个是考虑得装不下的情况，即剪的是右枝

现在考虑剪左枝的情况

左枝：即当前考虑的物品不装入背包的Cutting函数

如果当前已经选了的物品的总价值加上该物品后面可以装的物品的价值大于最优总价值

那么当前物品就没有必要装

为什么呢？这个可能很难理解

因为我装后面的物品得到的价值比当前的最优价值还大，那我当前物品完全就没有装的必要嘛

最优价值是更新的

贴个代码：

#include<bits/stdc++.h>
using namespace std;
#define max_v 105
int n;
int v[max_v],w[max_v];
int c;//背包容量
int cv=0;//当前装的物品的总价值
int cw=0;//当前装的物品的总重量
int bestv=0;//最优总价值
int bestx[max_v];//最优解
int x[max_v]={0};//当前解
int bound(int i)
{
int l=c-cw;
int b=cv;
while(w[i]<=l&&i<=n)
{
b+=v[i];
l-=w[i];
i++;
}
if(i<=n)
b+=l*v[i]/w[i];
return b;

}
void dfs(int i)
{
if(i>n)//搜完了一条路
{
for(int j=1;j<=n;j++)
bestx[j]=x[j];
bestv=cv;
}else
{
if(cw+w[i]<=c)//装得下
{
x[i]=1;//该物品装
cw+=w[i];
cv+=v[i];

        dfs(i+1);//搜索下一个物品

        x[i]=0;//回退
        cw-=w[i];
        cv-=v[i];
    }
    if(bound(i+1)>bestv)//最优总价值小于上界,当前已经选了的物品的总价值加上该物品后面可以装的物品的价值大于最优总价值,那么当前物品就没有必要装
    {
        x[i]=0;
        dfs(i+1);
    }
}

}
void putout()
{
int sum=0;
for(int i=1;i<=n;i++)
{
printf("%d “,bestx[i]);
if(bestx[i]==1)
sum+=w[i];
}
printf(“放入背包的物品重量为：%d 价值为:%d”,sum,bestv);
}
int main()
{
scanf(”%d %d",&n,&c);
for(int i=1;i<=n;i++)
{
scanf("%d %d",&v[i],&w[i]);
}
dfs(1);
putout();
return 0;
}
/*
输入：
5 10
6 2
3 2
6 4
5 6
4 5
输出：
1 1 1 0 0 放入背包的物品重量为：8 价值为:15
*/

01背包问题属于子集树问题，即每次都只要两种选择，物品选还是不选，有2的n次方个叶子结点

而排列树问题就是每次都有多种选择，比如下面要讲的n皇后问题，有n的阶乘个叶子节点

2. 经典样例二：N皇后问题

在Ｎ*Ｎ的棋盘上，放置Ｎ个皇后，要求每一横行，每一列，每一对角线上均只能放置一个皇后，求可能的方案及方案数。

怎么回溯：

比如先在空棋盘的第一行第一列放一个，然后看下一行，有没有合法的位置

所以现在有两种情况：

有合法的位置：那么就放，然后又看下一行，有没有合法的位置

没有合法的位置：回溯到上一个状态，即上一行，比如你在（0，0）放了一个，在（1，2）放了一个，现

在你要在第3行放一个，因为你前面放的两个皇后的位置，导致你在第三行无论放哪里都不合法，那这个时

候你就很尴尬了，你必须得回溯到第二行，本来是在（1，2）放的，你再在第二行找个合法的位置放一个

皇后，然后又继续放第三行，持续这个过程，直到最后一行都在合法的位置放了一个皇后

3. 经典样例三：油田问题

在这里插入图片描述

找到一个没有用过的油田就向这个油田的8个方向继续扩展，扩展的过程中遇到一个没有用过的新油田就标记为用过，然后又继续向它的8个方向扩展

就像*代表地面，油田代表地上有一个坑，你遍历整个地面，遇到一个没有水的坑你就往里面导水，水可以从8个方向流动，最后问你地上有几个大水坑。。。。

一样的问题

贴个代码：

#include<bits/stdc++.h>
using namespace std;
#define max_v 105
int n,m;
char a[max_v][max_v];//字符矩阵
int used[max_v][max_v];//该点被访问过就置1，开始初始化全0
int dx[8]={1,1,0,-1,-1,-1,0,1};//方向引导数组
int dy[8]={0,-1,-1,-1,0,1,1,1};
void dfs(int x,int y,int z)
{
if(x<0||x>=n||y<0||y>=m)//越界
return ;
if(used[x][y]>0||a[x][y]!=’@’)//被访问过或者不是油田
return ;
used[x][y]=z;//是油田，标记一下
for(int i=0;i<8;i++)
dfs(x+dx[i],y+dy[i],z);//8个方向继续找
}
int main()
{
while(~scanf("%d %d",&n,&m))
{
getchar();
for(int i=0;i<n;i++)
{
for(int j=0;j<m;j++)
{
scanf("%c",&a[i][j]);
}
getchar();
}
memset(used,0,sizeof(used));//初始化全0
int c=0;
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
if(used[i][j]0&&a[i][j]’@’)//没有访问过的油田
dfs(i,j,++c);
}
}
printf("%d\n",c);
}
}
/*
5 5
****@
@@@
@**@
@@@@
@@**@

2
*/

4. 经典样例四：素数环问题

在这里插入图片描述

题目要求你用1到20这20个数构成一个素数环，要求相邻的两个数的和是一个素数

把问题转换一下，这个不就是要求符合素数环特征的这20个数字的全排列吗？

其实就是一个全排列的思想加上一个素数的检测问题吗？

所以说，思想真的是很重要的东西，全排列的思想就是分治，让每个数轮流做第一个

关于全排序的问题请参考我的分治思想的那篇博客：https://www.cnblogs.com/yinbiao/p/9215525.html

贴个代码（所有知识都在代码里了）：

#include<bits/stdc++.h>
using namespace std;
#define max_v 105
int A[max_v];
int vis[max_v]={0};
int n;
int isp(int x)//判断x是不是一个素数
{
for(int i=2;i<=sqrt(x);i++)
{
if(x%i0)
return 0;
}
return 1;
}
void dfs(int cur)//确定第cur个空填什么数字
{
if(curn&&isp(A[0]+A[n-1]))//数字全部填完了且最后一个数加第一个数是一个素数，说明满足素数环的特征
{
for(int i=0;i<n;i++)//打印
printf("%d “,A[i]);
printf(”\n");
return ;
}else
{
for(int i=2;i<=n;i++)
{
if(!vis[i]&&isp(i+A[cur-1]))//i这个数没有被用过（因为素数环中每个数只可以出现一次）且它和前面填的那个数的和是素数
{
A[cur]=i;//第cur个空填i
vis[i]=1;//标记i用过
dfs(cur+1);//填下一个空
vis[i]=0;//回退
//回退的原因：每次回溯之后，要再进行搜索，要清除上次搜索做过的事情
}
}
}
}
int main()
{
scanf("%d",&n);//1~n个数
A[0]=1;//确定1的位置，要不然很麻烦，因为它是个环，环是可以转动的，环如果不确定一个数字的位置的话，重复的结果就是很多
dfs(1);//1表示现在确定第一个数字填什么（默认第一个数是1）
return 0;
}

5. 经典样例五：马的遍历问题

在n*m的棋盘中，马只能走“日” 字。马从位置(x, y)处出发，把棋盘的每一格都走一次，且只走一次。找出所有路径。（象棋棋盘）

这个问题跟油田问题没有什么区别，都是同样一类问题（可以说是模板代码了）

不同的地方：

1.马只能走日字，而油田问题可以走8个方向，所以需要改一下方向引导数组

Cutting函数：

1.别走出棋盘界限

2.每个点只能走一次

走过的点数==n*m的话，就是找到一种走法了，输出这种走法

这个样例我就是不放代码了，因为这个问题和油田问题都属于同一类型的问题，模板都是一样的，要改的地

方主要就是方向引导数组

6. 经典样例六：图m的着色问题

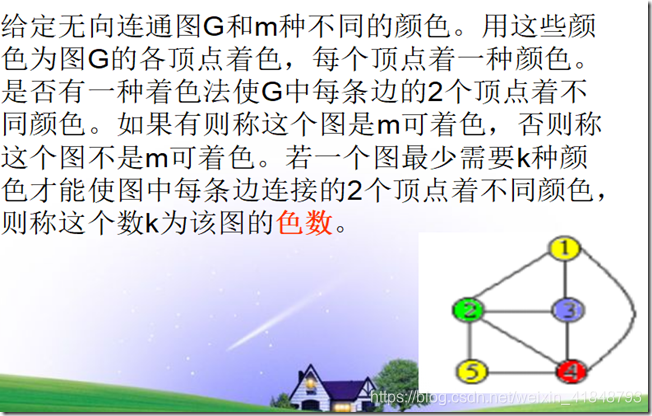
在这里插入图片描述
题目要求使得每个边的两个点都是不同的颜色

题目可以问你至少要多少种颜色才能给图着色完毕，也可以问你具体的着色方案（本题）

设计数据结构：

用邻接矩阵存无向图

x【i】=j，第i个点用第j中颜色

CUtting函数：

条件：

相邻的点不能使用同一种颜色，即同一条边的点不能使用同一种颜色

即已经着色过的点的相邻的点又用同一种颜色，那么这个时候就需要进行Cutting操作了

递归结束条件：最后一个点着色完毕，这个时候说明你找到一种着色的方案了，你可以继续接着找（找全部解的话），也可以直接返回（找任意解的话）

贴个代码（所有细节，思想在代码李都有体现，代码看懂了，然后刷几道图m着色的题，这个问题就是掌握了，但是这个问题的变形题的话，就要继续多刷变形题了）

#include<bits/stdc++.h>
using namespace std;
#define max_v 105
int a[max_v][max_v];
int x[max_v+1];// x][i]=j 表示点i用j颜色
int sum=0;//着色方案数
int n,m;//点数，颜色数
int ok(int t,int i)
{
for(int j=1;j<t;j++)
{
if(a[t][j]&&x[j]i)//t,j相邻且同色
return 0;//这是t不能用i着色
}
return 1;
}
void dfs(int t,int m)
{
if(t>n)//搜到了叶子节点
{
sum++;
printf(“第%d种方案:”,sum);
for(int i=1;i<=n;i++)//打印具体着色方案
printf("%d “,x[i]);
printf(”\n");
}else
{
for(int i=1;i<=m;i++)
{
if(ok(t,i))//t能用i着色的话
{
x[t]=i;//着色
dfs(t+1,m);//搜索给下一个点着什么色
}
}
}
}
int main()
{
scanf("%d %d",&n,&m);
memset(a,0,sizeof(a));//初始化置0
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
scanf("%d",&a[i][j]);//构造图，下标从1开始
}
}
for(int i=0;i<=n;i++)
x[i]=0;//每个点初始化置0色
dfs(1,m);//开始给第一个点置色
if(sum0)
printf("%d种颜色不可着色成功\n",m);
return 0;
}
/*
输入：
3 3
1 1 1
1 1 1
1 1 1