boosting、bagging、GBDT等集成学习算法的简单比较_gbdt是一种bagging方法-优快云博客

本文链接：https://blog.youkuaiyun.com/weixin_41830122/article/details/89280410

本文深入探讨了GBDT算法在处理分类问题时，当采用指数损失函数时，其算法原理与Adaboost算法的相似性。通过详细的分类图和代码示例，清晰地展示了两种算法之间的联系及集成学习的多种方法。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

分类图：

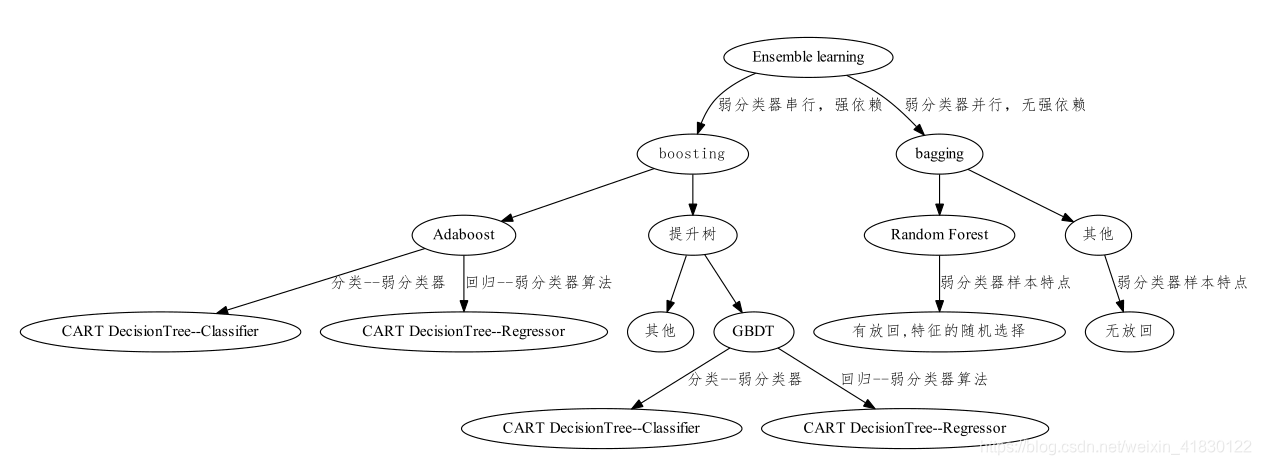
备注：GBDT算法做分类问题时，损失函数如果是指数损失函数时，则算法原理与Adaboost算法相同。

分类图制作代码如下：

from graphviz import Digraph
fig=Digraph(comment='Ensemble learning')
fig.node('a','Ensemble learning')
fig.node('b','boosting',fontname='FangSong')
fig.node('c','bagging')
fig.node('d','Adaboost')
fig.node('f',u'提升树',fontname='FangSong')
fig.node('F',u'其他',fontname='FangSong')
fig.node('e','GBDT')
fig.node('g','Random Forest')
fig.node('h',u'其他',fontname='FangSong')
fig.node('i','CART DecisionTree--Classifier')
fig.node('I','CART DecisionTree--Classifier')
fig.node('j','CART DecisionTree--Regressor')
fig.node('J','CART DecisionTree--Regressor')
fig.node('k',u'有放回,特征的随机选择',fontname='FangSong')
fig.node('l',u'无放回',fontname='FangSong')

fig.edge('a','b',label=u'弱分类器串行，强依赖',fontname='FangSong')
fig.edge('a','c',label=u'弱分类器并行，无强依赖',fontname='FangSong')
fig.edges(['bf','bd','fe','fF','ch','cg'])
fig.edge('d','i',label=u'分类--弱分类器',fontname='FangSong')
fig.edge('d','j',label=u'回归--弱分类器算法',fontname='FangSong')
fig.edge('e','I',label=u'分类--弱分类器',fontname='FangSong')
fig.edge('e','J',label=u'回归--弱分类器算法',fontname='FangSong')
fig.edge('g','k',label=u'弱分类器样本特点',fontname='FangSong')
fig.edge('h','l',label=u'弱分类器样本特点',fontname='FangSong')

fig.view() #显示pdf图
fig.render(u'集成学习分类图',view=True) #保存并显示pdf图