一维前缀和与二维前缀和问题

前缀和主要用于解决求数组中从第n位到第m位的和或者从(x1,y1)到(x2,y2)之间的数值和。

对于一维数组：数组中从第n位到第m位的和等于 S[m] - S[n-1]

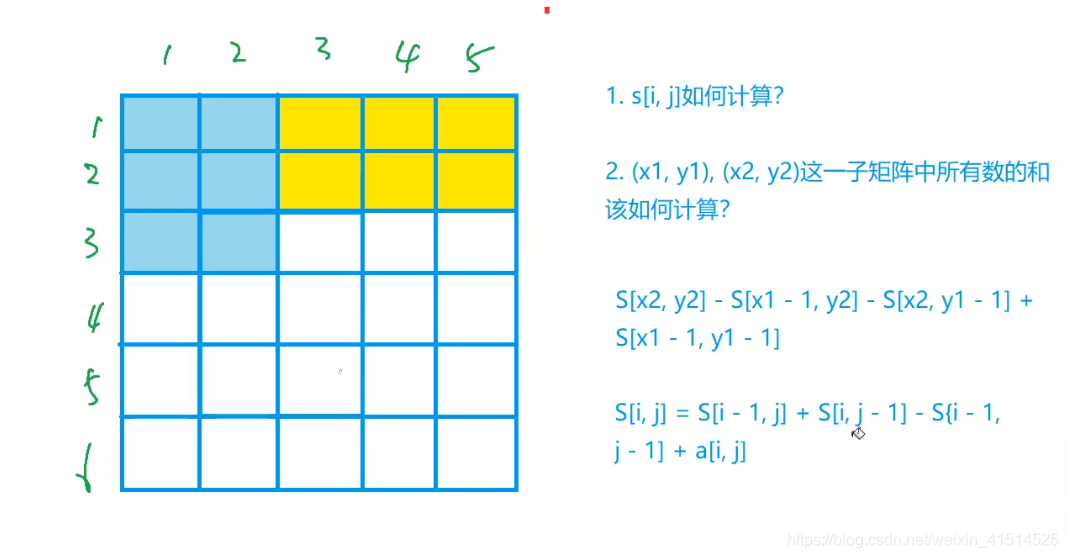
对于二维数组：数组中从(x1,y1)到(x2,y2)之间的数值和等于 S[x2][y2] - S[x2][y1-1] - S[x1-1][y2] + S[x1-1][y1-1]

注意：
    1.对于S[]数组的存放要从s[1]或者s[1][1]开始,这样一是为了便于统一表达式,同时存放源数据的数组也最好从a[1]或者a[1][1]开始存放，二是S[x][y]的推到中用到[x-1]和[y-1],为防止数组越界,数组从1开始存数据。
    2.S[]数组可以置为全局变量，这样的话数组的内容会被自动初始化为0。
    3.在一维数组求S[i]的时候，S[i] = S[i-1] + a[i - 1]
    4.在一维数组求S[i][j]的时候,S[i][j] = S[i-1][j] + S[i][j-1] - S[i-1][j-1] + a[i][j]
    5.前缀和的优势在于一次O(n)或者O(n^2)(n是数组中元素个数)迭代操作求出所以的s[i]或者s[i][j],之后求数组中从第n位到第m位的和或者数组中从(x1,y1)到(x2,y2)之间的数值和就只是O(1)的复杂度了。
    6.为了代码书写简单: 二维前缀和的数组置为全局变量，且二维前缀的i和j从1开始存放元素！！！！！！！！

二维前缀和：

输入一个n行m列的整数矩阵，再输入q个询问，每个询问包含四个整数x1, y1, x2, y2，表示一个子矩阵的左上角坐标和右下角坐标。

对于每个询问输出子矩阵中所有数的和。

输入格式

第一行包含三个整数n，m，q。

接下来n行，每行包含m个整数，表示整数矩阵。

接下来q行，每行包含四个整数x1, y1, x2, y2，表示一组询问。

输出格式

共q行，每行输出一个询问的结果。

数据范围

1≤n,m≤10001≤n,m≤1000,
1≤q≤1000001≤q≤100000,
1≤x1≤x2≤n1≤x1≤x2≤n,
1≤y1≤y2≤m1≤y1≤y2≤m,
−1000≤矩阵内元素的值≤1000−1000≤矩阵内元素的值≤1000

输入样例：

3 4 3
1 7 2 4
3 6 2 8
2 1 2 3
1 1 2 2
2 1 3 4
1 3 3 4

输出样例：

17
27
21

#include<iostream>
using namespace std;
const int N = 1010;
int a[N][N];  // 全局变量的数组其中的各元素自动初始化为0
long long s[N][N];
int main(){
    int n,m,q,x1,y1,x2,y2;
    scanf("%d%d%d",&n,&m,&q);
    for (int i = 1; i <= n ; ++i)
    for (int j = 1; j <= m ; ++j)
    scanf("%d",&a[i][j]);
    for (int i = 1; i <= n; ++i)
    for (int j = 1; j <= m; ++j)
    s[i][j] = s[i][j-1] + s[i-1][j] - s[i-1][j-1] + a[i][j]; //计算s[i][j]
    for(int i = 0; i < q; ++i){
        scanf("%d%d%d%d",&y1,&x1,&y2,&x2);
        printf("%d\n",s[y2][x2] - s[y2][x1 - 1] - s[y1 - 1][x2] + s[y1 - 1][x1 - 1]);
        
    }
    return 0;
}

一维前缀和：

输入一个长度为n的整数序列。

接下来再输入m个询问，每个询问输入一对l, r。

对于每个询问，输出原序列中从第l个数到第r个数的和。

输入格式

第一行包含两个整数n和m。

第二行包含n个整数，表示整数数列。

接下来m行，每行包含两个整数l和r，表示一个询问的区间范围。

输出格式

共m行，每行输出一个询问的结果。

数据范围

1≤l≤r≤n1≤l≤r≤n,
1≤n,m≤1000001≤n,m≤100000,
−1000≤数列中元素的值≤1000−1000≤数列中元素的值≤1000

输入样例：

5 3
2 1 3 6 4
1 2
1 3
2 4

输出样例：

3
6
10

#include<iostream>
using namespace std;
int main(){
    int m ,n,start,end;
    const int N = 100010;
    int a[N];
    long long s[N];
    s[0]  = 0;
    scanf("%d%d",&n,&m);
    for(int i = 0; i < n; ++i)  scanf("%d",&a[i]);
    for (int i = 1; i <= n ; ++i) s[i] = s[i-1] + a[i - 1];
    for (int i = 0; i < m ; ++i){
        scanf("%d",&start);
        scanf("%d",&end);
        printf("%d\n",s[end] - s[start - 1]);
    }
    return 0;
}