leetcode 746. 使用最小花费爬楼梯(python3)

最新推荐文章于 2024-11-22 10:12:02 发布

算法黑哥

最新推荐文章于 2024-11-22 10:12:02 发布

阅读量334

点赞数

CC 4.0 BY-SA版权

分类专栏： leetcode刷题

本文链接：https://blog.youkuaiyun.com/weixin_41504611/article/details/104800435

leetcode刷题专栏收录该内容

59 篇文章

订阅专栏

本文解析了如何在给定的体力花费数组中找到达到楼层顶部的最低花费路径。通过动态规划思想，比较从前一步和前两步过来的花费，找到最省体力的爬楼梯策略。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

746. 使用最小花费爬楼梯

数组的每个索引做为一个阶梯，第 i个阶梯对应着一个非负数的体力花费值 costi。

每当你爬上一个阶梯你都要花费对应的体力花费值，然后你可以选择继续爬一个阶梯或者爬两个阶梯。

您需要找到达到楼层顶部的最低花费。在开始时，你可以选择从索引为 0 或 1 的元素作为初始阶梯。

示例 1:

输入: cost = [10, 15, 20]
输出: 15
解释: 最低花费是从cost[1]开始，然后走两步即可到阶梯顶，一共花费15。
示例 2:

输入: cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1]
输出: 6
解释: 最低花费方式是从cost[0]开始，逐个经过那些1，跳过cost[3]，一共花费6。
注意：

cost 的长度将会在 [2, 1000]。
每一个 cost[i] 将会是一个Integer类型，范围为 [0, 999]。

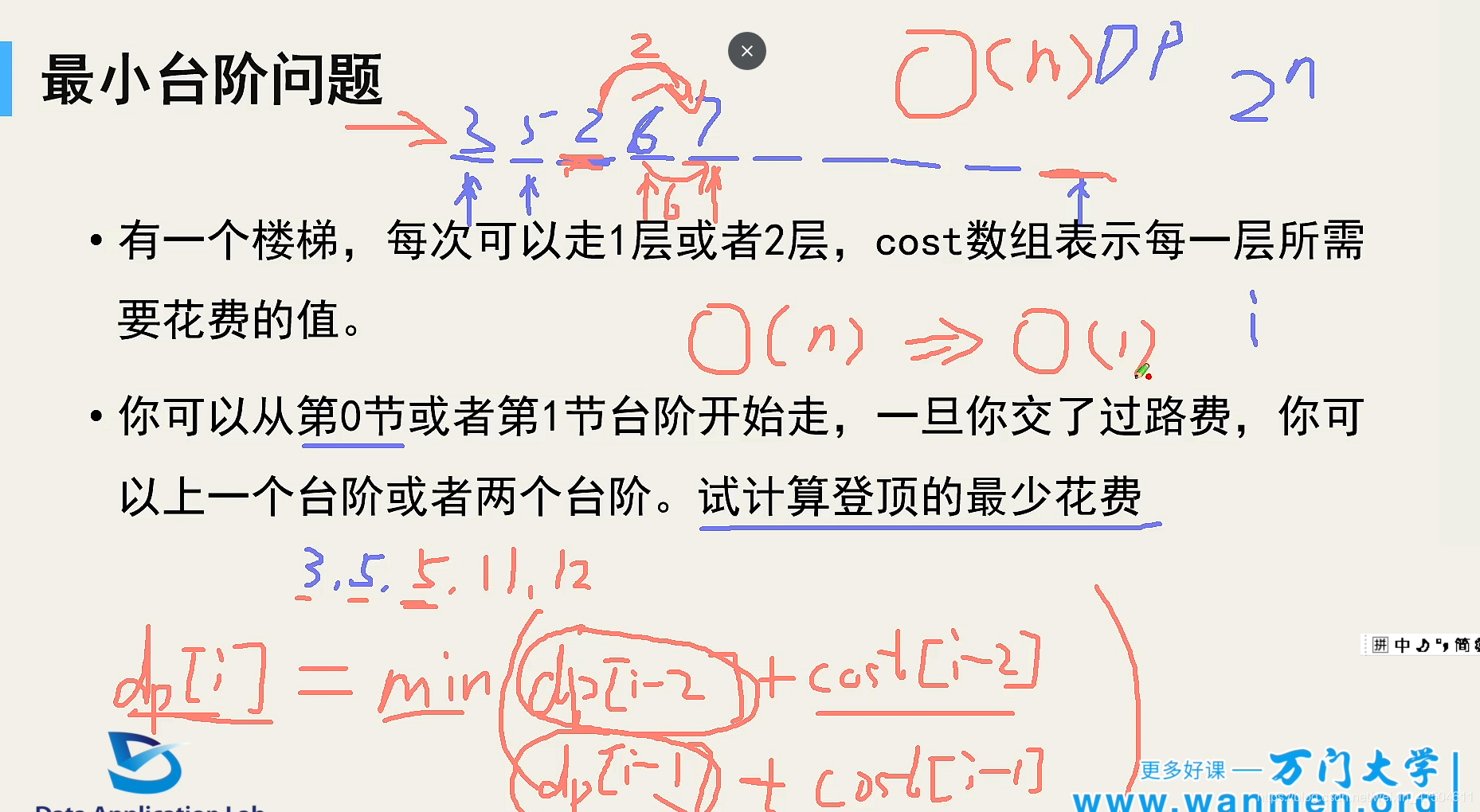
在这里插入图片描述

思路
到达当前台阶时判断下从前一个台阶过来省事，还是从前一个的前一个过来省事，一直累加到最后一个台阶完，最小值就是最省体力的。用p1和p2表示前两个和前一个台阶所耗费的体力，一遍循环就可以了。

class Solution(object):
    def minCostClimbingStairs(self, cost):
        a , b = 0 , 0
        for i in range(2,len(cost)+1):
            a , b = b, min(a+cost[i-2],b+cost[i-1])
        return b