动手学习深度学习——卷积神经网络基础

  这个系列确实不太好写，训练网络准备数据等等都需要花费不少时间，所以更新会比较慢一些，orz。
  本博客的主要内容还是偏向于卷积神经网络(CNN)，至于其他种类的深度学习，这里暂不涉及。如果觉得有用，可以顺手点个赞，也欢迎在留言板讨论交流，文中如有错误，请指出说明，谢谢。

1. 深度学习基本网络层

1.1 卷积层

  1). 卷积层的工作原理
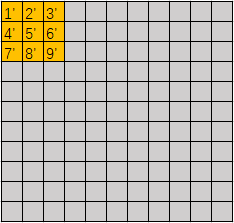
  卷积计算的过程如下图所示，灰色的代表图像，每个格子代表一个像素点，橙色的是卷积核。卷积核在图像中移动，卷积核上1-9的位置都有对应的系数，每个系数都乘以对应图像位置的数值(如1’-9’)，然后相加后作为结果，存在卷积核中心对应的图像位置(如图中的5’)。然后根据设定好的步长 $s$ ，卷积核向右移动 s 个像素(如图为步长为1的时候卷积核移动的结果)，如果超出图像范围就换行从头开始。
  什么叫边缘填充(padding)呢？简单来说就是在卷积前对原始图像的周围进行填0或其他数值(如下图的绿色区域)。通过适当的填充，可以让图像在卷积后的尺寸保持不变，这时进行边缘填充最常见的目的。
    

  在深度学习里，常说的卷积层输入通道和输出通道又是什么意思呢？众所周知，通常彩色图像都不是简单的$m\times n$的二维数据，而是$m\times n\times 3$的三维数据，图像中也成为3通道，每个$m\times n\times 1$分别代表R、G、B颜色通道，如果把这样的三维数据输入卷积层，就称卷积层的输入是3通道的(input_channels=3)。
  这时，假设卷积层卷积核的尺寸为$3\times 3$，系数也初始化设定好了，要怎么对三维数据进行卷积呢？很简单，也把卷积核扩充为三维的，且通道数和卷积层的输入通道数相同，也就是$3\times 3\times 3$。其中，3个$3\times 3\times 1$模块的系数是一模一样的，相当于将原来的$3\times 3$卷积核沿第三个维度复制了三份。这时候，再对图像进行和2维卷积一样的操作，$3\times 3\times 3$卷积核每个位置的系数乘上对应位置的数据，并全部相加，就计算得到卷积核中心位置的数值结果。细心的读者可能发现了，这么做之后，原来输入的$m\times n\times k$维的数据，就变成了$m^{\prime }\times n^{\prime }\times 1$，也就是多通道的数据变成了单通道了。用深度学习的术语来说，就是数据输入卷积层后，经过一个卷积核卷积，就生成一个特征图(feature map)。那么，如果有$k^{\prime }$个不同的卷积核，就能生成$k^{\prime }$个feature map，把所有的feature map累加起来，就形成了卷积层的输出$m^{\prime }\times n^{\prime }\times k^{\prime }$