33. N皇后问题（DFS）

描述

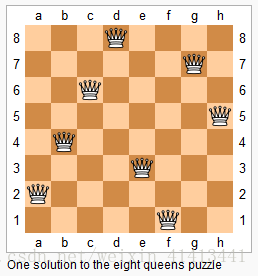
n皇后问题是将n个皇后放置在n*n的棋盘上，皇后不能处在同一行、同一列、或同一斜线上，才能保证皇后彼此之间不能相互攻击。

给定一个整数n，返回所有不同的n皇后问题的解决方案。

每个解决方案包含一个明确的n皇后放置布局，其中“Q”和“.”分别表示一个女王和一个空位置。

您在真实的面试中是否遇到过这个题？  是

样例

对于4皇后问题存在两种解决的方案：

[

    [".Q..", // Solution 1

     "...Q",

     "Q...",

     "..Q."],

    ["..Q.", // Solution 2

     "Q...",

     "...Q",

     ".Q.."]

]

分析：
本质：深度优先搜索（DFS）,隐式图空间，时间复杂度N^N(状态空间）

搜索过程：

我们在试探的过程中，皇后的放置需要检查他的位置是否和已经放置好的皇后发生冲突，为此需要以及检查函数来检查当前要放置皇后的位置，是不是和其他已经放置的皇后发生冲突

假设有两个皇后被放置在（i，j）和（k，l）的位置上，明显，当且仅当|i-k|=|j-l| 时，两个皇后才在同一条对角线上。

当i=k时在同一行上，j=l时在同一列上

（1）先从首位开始检查，如果不能放置，接着检查该行第二个位置，依次检查下去，直到在该行找到一个可以放置一个皇后的地方，然后保存当前状态，转到下一行重复上述方法的检索。 
（2）如果检查了该行所有的位置均不能放置一个皇后，说明上一行皇后放置的位置无法让所有的皇后找到自己合适的位置，因此就要回溯到上一行，重新检查该皇后位置后面的位置。

代码：

class Solution {
public:
    /*
     * @param n: The number of queens
     * @return: All distinct solutions
     */
    vector<vector<string>> solveNQueens(int n) {
        // write your code here
         vector<vector<string> > res;
        vector<int> pos(n, -1);
        solveNQueensDFS(n,pos, 0, res);
        return res;
    }
    void solveNQueensDFS(int n,vector<int> &pos, int row, vector<vector<string> > &res) {
        if (row == n) {
            vector<string> out(n, string(n, '.'));
            for (int i = 0; i < n; ++i) {
                out[i][pos[i]] = 'Q';
            }
            res.push_back(out);
        } else {
            for (int col = 0; col < n; ++col) {
                if (isValid(pos, row ,col)) {
                    pos[row] = col;
                    solveNQueensDFS(n,pos, row + 1, res);
                    pos[row] = -1;
                }
            }
        }
    }
    bool isValid(vector<int> &pos, int row, int col) {
        for (int i = 0; i < row; ++i) {
            if (col == pos[i] || abs(row - i) == abs(col - pos[i])) {
                return false;
            }
        }
        return true;
    }
};