【离线强化学习】IQL（Implicit Q-learning）+D4RL

原创已于 2025-12-17 02:03:59 修改 · 576 阅读

25 ·

CC 4.0 BY-SA版权

文章标签：

#离线强化学习 #强化学习 #深度学习 #python #pytorch #人工智能 #IQL

于 2025-12-17 02:03:08 首次发布

IQL算法简介

在在线强化学习（OnlineRL）中，Q函数的更新如下：
$Q(s,a)\leftarrow Q(s,a)+\alpha(r+\gamma \max_{a'}(s',a')-Q(s,a))$ 使用函数近似（如神经网络）来拟合Q函数，并通过最小化时序差分误差来更新：
$L_Q(\theta) = \mathbb{E}_{(s,a,r,s') \sim D} \left[ \left( r + \gamma \max_{a'} Q_{\theta}(s', a') - Q_{\theta}(s, a) \right)^2 \right]$ 而在离线强化学习（OfflineRL）的设定中， $max⁡a′Qθ(s′,a′)\max_{a'} Q_{\theta}(s', a')$ 要求我们对下一个状态 $s^{'}$ 的所有可能动作 $a^{'}$ 求最大值。然而，我们的数据集只包含行为策略 $πβ\pi_{\beta}$ 所采取的动作，因此对于某些 $s^{'}$ ，我们可能没有见过最优动作。由于函数近似器的泛化性，它可能会对未见过的动作给出过高估计，从而导致策略学习到次优甚至危险的动作。

IQL的核心思想是：我们只利用数据集中出现的动作来学习价值函数，避免查询那些未出现动作的Q值。具体来说，IQL通过以下三个步骤实现：

IQL引入一个状态价值函数 $V (s)$ ，并定义它应该近似于在状态 $s$ 下，数据集中高 $Q$ 值的动作所对应的 $Q$ 值的期望。为此，IQL使用期望回归（expectile regression）来训练 $V (s)$ 。
$LV(ψ)=E(s,a)∼D[L2τ(Qθ(s,a)−Vψ(s))]L_V(\psi) = \mathbb{E}_{(s,a) \sim D} \left[ L_2^{\tau} \left( Q_{\theta}(s, a) - V_{\psi}(s) \right) \right]$ $L2τ(u)=∣τ−1(u<0)∣⋅u2L_2^\tau(u) = |\tau - \mathbb{1}(u<0)| \cdot u^2$ 这里， $τ∈(0,1)\tau \in (0,1)$ 是一个超参数。当 $τ=0.5\tau = 0.5$ 时，就是标准的均方误差；当 $τ>0.5\tau > 0.5$ 时，损失函数会更多地惩罚 $V (s)$ 低于 $Q (s, a)$ 的情况，从而鼓励 $V (s)$ 逼近 $Q (s, a)$ 的上分位数（即较大的Q值）。通过这种方式， $V (s)$ 学习到的是在状态 $s$ 下，数据集中那些高Q值动作对应的Q值的条件期望。注意，这个更新只依赖于数据集中存在的 $(s, a)$ 对，不涉及任何最大化操作。
用 $V (s^{'})$ 来代替 $max_{a'} Q(s',a')$ ：
$LQ(θ)=E(s,a,r,s′)∼D[(r+γVψ(s′)−Qθ(s,a))2]L_Q(\theta) = \mathbb{E}_{(s,a,r,s') \sim D} \left[ \left( r + \gamma V_{\psi}(s') - Q_{\theta}(s,a) \right)^2 \right]$ 这里，目标值 $\gamma V_{\psi}(s')$ 不依赖于动作 $a^{'}$ ，因此不会出现对未见动作的查询。同时，由于 $V (s^{'})$ 已经代表了数据集中高Q值动作的期望，所以可以传播高回报的信息。
策略 $π\pi$ 通过一个类似于优势加权行为克隆（Advantage-Weighted Regression, AWR）的方式来学习：
$Lπ(ϕ)=E(s,a)∼D[exp⁡(β(Qθ(s,a)−Vψ(s)))⋅log⁡πϕ(a∣s)]L_{\pi}(\phi) = \mathbb{E}_{(s,a) \sim D} \left[ \exp\left(\beta \left(Q_{\theta}(s,a) - V_{\psi}(s)\right)\right) \cdot \log \pi_{\phi}(a|s) \right]$ 其中， $β>0\beta > 0$ 是一个超参数。注意，优势函数 $A (s, a) = Q (s, a) - V (s)$ 衡量了动作 $a$ 相对于状态 $s$ 下平均好动作水平的优势。因此，权重 $exp⁡(β⋅A(s,a))\exp(\beta \cdot A(s,a))$ 会对那些优势高的动作赋予更大的权重，从而使得策略更倾向于选择数据集中优势高的动作。

与CQL相比

特性	IQL	CQL	优胜方
核心理念	回避 OOD 查询	惩罚 OOD 高估	视场景而定
策略约束	隐式（自然）	显式（正则化）	IQL 更优雅
理论保证	较弱但实用	强理论下界	CQL 更严谨
实现简单性	简单直观	中等复杂度	IQL 更易实现
连续动作	优秀	良好	IQL 更适合
离散动作	良好	优秀	CQL 更直接
数据效率	高（利用好数据）	保守（避免坏数据）	互补
超参数敏感	中等（τ）	高（α）	IQL 更稳定
计算效率	中等	较高	IQL 更高效
SOTA 性能	多任务领先	部分任务领先	总体 IQL 稍优

代码

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim

import numpy as np
import random
import d4rl
import math
import gym

from torch.distributions import Normal

from matplotlib.ticker import MaxNLocator
import matplotlib.pyplot as plt


class QNet(nn.Module):

    def __init__(self, obs_dims, act_dims):
        super().__init__()

        self.mlp = nn.Sequential(
            nn.Linear(obs_dims + act_dims, 512),
            nn.LeakyReLU(),
            nn.LayerNorm(512),
            nn.Linear(512, 256),
            nn.LeakyReLU(),
            nn.LayerNorm(256),
            nn.Linear(256, 128),
            nn.LeakyReLU(),
            nn.LayerNorm(128),
            nn.Linear(128, 64),
            nn.LeakyReLU(),
            nn.LayerNorm(64),
            nn.Linear(64, 1)
        )

    def forward(self, obs, act):

        x = torch.cat([obs, act], dim=-1)

        return self.mlp(x)


class VNet(nn.Module):
    
    def __init__(self, obs_dims):
        super().__init__()

        self.mlp = nn.Sequential(
            nn.Linear(obs_dims, 512),
            nn.LeakyReLU(),
            nn.LayerNorm(512),
            nn.Linear(512, 256),
            nn.LeakyReLU(),
            nn.LayerNorm(256),
            nn.Linear(256, 128),
            nn.LeakyReLU(),
            nn.LayerNorm(128),
            nn.Linear(128, 64),
            nn.LeakyReLU(),
            nn.LayerNorm(64),
            nn.Linear(64, 1)
        )
    
    def forward(self, obs):

        return self.mlp(obs)
    

class GasPolicy(nn.Module):

    def __init__(self, obs_dims, act_dims,
                log_std_min=-5, log_std_max=2):
        super().__init__()

        self.log_std_min = log_std_min
        self.log_std_max = log_std_max

        self.mlp = nn.Sequential(
            nn.Linear(obs_dims, 512),
            nn.LeakyReLU(),
            nn.LayerNorm(512),
            nn.Linear(512, 256),
            nn.LeakyReLU(),
            nn.LayerNorm(256),
            nn.Linear(256, 128),
            nn.LeakyReLU(),
            nn.LayerNorm(128),
            nn.Linear(128, 64),
            nn.LeakyReLU(),
            nn.LayerNorm(64),
            nn.Linear(64, 2 * act_dims),
        )

    def forward(self, obs):

        atanh_mu, log_std = self.mlp(obs).chunk(2, dim=-1)

        log_std = torch.clamp(log_std, self.log_std_min, self.log_std_max)
        
        return atanh_mu.tanh(), log_std.exp()
    

class IQLAgent:

    def __init__(self, env, device="cpu", gamma=0.99, expectile=0.7, temperature=3.0, lr=3e-4):
        
        self.obs_dims = env.observation_space.shape[0]
        self.act_dims = env.action_space.shape[0]

        self.device = device
        self.gamma = gamma
        self.expectile = expectile
        self.temperature = temperature

        self.actor = GasPolicy(self.obs_dims, self.act_dims).to(device)

        self.q1_net = QNet(self.obs_dims, self.act_dims).to(device)
        self.q2_net = QNet(self.obs_dims, self.act_dims).to(device)

        self.value_net = VNet(self.obs_dims).to(device)

        self.actor_optimizer = optim.AdamW(self.actor.parameters(), lr=lr)
        self.q1_optimizer = optim.AdamW(self.q1_net.parameters(), lr=lr)
        self.q2_optimizer = optim.AdamW(self.q2_net.parameters(), lr=lr)
        self.value_optimizer = optim.AdamW(self.value_net.parameters(), lr=lr)

    @staticmethod
    def expectile_loss(diff, expectile):
        weight = torch.where(diff > 0, expectile, 1 - expectile)
        return weight * diff.pow(2)

    def select_action(self, obs, greedy=False):
        
        with torch.no_grad():

            obs = torch.tensor(obs, dtype=torch.float, device=self.device)
            
            if greedy:
                mu, _ = self.actor(obs)
                return mu.cpu().numpy()
            else:
                mu, std = self.actor(obs)
                normal_dist = Normal(mu, std)
                a = normal_dist.sample()
                return a.cpu().numpy().clip(-1, 1)

    def train(self, dataset, batch_size=256):
        
        observations, actions, rewards, next_observations, dones = (
            torch.tensor(dataset.get("observations"), dtype=torch.float, device=self.device),
            torch.tensor(dataset.get("actions"), dtype=torch.float, device=self.device),
            torch.tensor(dataset.get("rewards"), dtype=torch.float, device=self.device).reshape(-1, 1),
            torch.tensor(dataset.get("next_observations"), dtype=torch.float, device=self.device),
            torch.tensor(dataset.get("terminals"), dtype=torch.float, device=self.device).reshape(-1, 1),
        )
        perm = torch.randperm(len(observations))

        observations, actions, rewards, next_observations, dones = (
            observations[perm], actions[perm], rewards[perm],
            next_observations[perm], dones[perm]
        )

        data_size = observations.shape[0]
        if data_size % batch_size == 0:
            mini_epochs = data_size // batch_size
        else:
            mini_epochs = (data_size // batch_size) + 1
        
        v_loss_list, q_loss_list, actor_loss_list = [], [], []

        for m_ep in range(mini_epochs):
            start = m_ep * batch_size
            end = min(data_size, (m_ep + 1) * batch_size)

            obs, act, r, next_obs, d = (
                observations[start:end], actions[start:end], rewards[start:end],
                next_observations[start:end], dones[start:end]
            )

            # ---------------------- Value Update ---------------------- #
            with torch.no_grad():
                q1 = self.q1_net(obs, act)
                q2 = self.q2_net(obs, act)
                q = torch.min(q1, q2)
            
            v = self.value_net(obs)
            v_loss = self.expectile_loss(q - v, self.expectile).mean()

            self.value_optimizer.zero_grad()
            v_loss.backward()
            self.value_optimizer.step()
            v_loss_list.append(v_loss.item())

            # ---------------------- Q Net Update ---------------------- #
            with torch.no_grad():
                v_next = self.value_net(next_obs)
                q_target = r + self.gamma * (1.0 - d) * v_next

            q1_pred = self.q1_net(obs, act)
            q2_pred = self.q2_net(obs, act)

            q1_loss = F.mse_loss(q1_pred, q_target)
            q2_loss = F.mse_loss(q2_pred, q_target)
            q_loss = q1_loss + q2_loss

            self.q1_optimizer.zero_grad()
            self.q2_optimizer.zero_grad()
            q_loss.backward()
            self.q1_optimizer.step()
            self.q2_optimizer.step()
            q_loss_list.append(q_loss.item())

            # ---------------- Actor Update (AWR-style) ---------------- #
            with torch.no_grad():
                adv = q - v
                weights = torch.exp(adv * self.temperature).clamp(max=100.0)

            mu, std = self.actor(obs)

            normal_dist = Normal(mu, std)

            log_prob = normal_dist.log_prob(act).sum(dim=-1, keepdim=True)

            actor_loss = -(weights * log_prob).mean()

            self.actor_optimizer.zero_grad()
            actor_loss.backward()
            self.actor_optimizer.step()
            actor_loss_list.append(actor_loss.item())
        
        return (
            sum(v_loss_list) / len(v_loss_list),
            sum(q_loss_list) / len(q_loss_list),
            sum(actor_loss_list) / len(actor_loss_list)
        )


def evaluate(agent, env, episodes=10, greedy=True):
    avg_reward = 0.0
    for _ in range(episodes):
        state = env.reset()
        done = False
        while not done:
            action = agent.select_action(state, greedy)
            state, reward, done, _ = env.step(action)
            avg_reward += reward
    avg_reward /= episodes
    return avg_reward


def plot_training_curve(loss_dict, reward_list):

    all_items = list(loss_dict.items()) + [("Eval Reward", reward_list)]
    n_subplots = len(all_items)

    ncols = math.ceil(math.sqrt(n_subplots))
    nrows = math.ceil(n_subplots / ncols)

    fig, axes = plt.subplots(nrows, ncols, figsize=(4*ncols, 3*nrows))
    axes = axes.flatten()

    epochs = range(1, len(reward_list)+1)

    for i, (name, data) in enumerate(all_items):
        axes[i].plot(epochs, data, label=name)
        axes[i].set_title(name)
        axes[i].xaxis.set_major_locator(MaxNLocator(integer=True))

    for j in range(i+1, len(axes)):
        axes[j].axis('off')

    plt.tight_layout()
    plt.show()


def set_seed(seed):

    random.seed(seed)
    np.random.seed(seed)
    torch.manual_seed(seed)
    torch.cuda.manual_seed(seed)
    torch.cuda.manual_seed_all(seed)
    torch.backends.cudnn.deterministic = True
    torch.backends.cudnn.benchmark = False


def main(episodes=100, batch_size=256, device="cpu", seed=2025):

    set_seed(seed)

    env = gym.make("bullet-halfcheetah-medium-expert")
    env.seed(seed)
    dataset = env.get_dataset()
    agent = IQLAgent(env, device=device)

    loss_dict = {"V Loss": [], "Q Loss": [], "Actor Loss": []}
    reward_list = []

    for ep in range(1, episodes+1):
        v_loss, q_loss, actor_loss = agent.train(dataset, batch_size)
        avg_reward = evaluate(agent, env)

        loss_dict["V Loss"].append(v_loss)
        loss_dict["Q Loss"].append(q_loss)
        loss_dict["Actor Loss"].append(actor_loss)
        reward_list.append(avg_reward)

        print(
            f"""[Epoch {ep:03d}]
            |* V Loss: {v_loss:.4f}
            |* Q Loss: {q_loss:.4f}
            |* Actor Loss: {actor_loss:.4f}
            |* Eval Reward: {avg_reward:.2f}
            """
        )

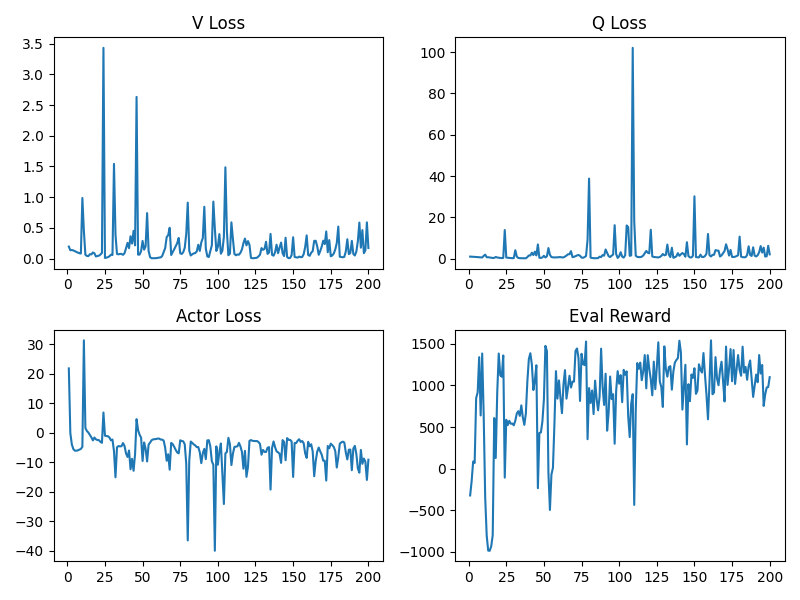
    plot_training_curve(loss_dict, reward_list)


if __name__ == "__main__":

    main(episodes=200, batch_size=8 * 2048, device="mps")