最长递增子序列

动态规划：是求解决策过程的最优方法，是把多阶段过程转为多阶段过程然后逐个求解，这就是动态规划；

应用领域：库存管理、资源分配、设备更新、排序、装载、空间和时间转化及递推关系；

题目描述：输入一个整数序列，求出其最长子序列的长度，使得子序列里前一项总比后一项小。（注：子序列的每一项都属于原数列，且不一定连续）举个例子，假如输入的数列为3 6 1 4 2 8 9 5 7，那么它的最长子序列一共有五个（3 6 8 9；3 4 8 9；1 2 8 9；1 2 5 7；3 4 5 7），最长子序列的长度是4。

解答：（1）暴力求解法

将每一个数字看为最长递增子序列最后一个元素，那么可以用有向图的深度优先遍历来求解，但是复杂度太高；设原序列的长度为n，那么就有O(n)个整数需要被搜索，每层搜索又会递归到O(n)个下一层搜索，而搜索又有O(n)层，也就是说数据如果坑，时间复杂度可能达到O(n^n)。要是n值有20，计算机就已经算的够累了，更不说n=2000的情况了。这就到了动态规划大显神通的时候了。先说一句，使用动态规划要注意空间和时间之间的转化以及递推的关系。

（2）动态规划找递推关系

1. 首先设一个数组arr_2用来保存对应每个数为最后的最大长度，初始全为1

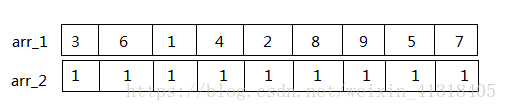
 2. 遍历n个数，第i个数对应的长度arr_2[1]是，遍历0到i-1之间的arr_1，找到小于arr_1[1]的最大值下表为index，则arr_2[i] = arr_2[index]+1;

代码： 

#include<stdio.h>
#include<malloc.h>


int fun(int *arr_1,int *arr_2,int len)
{
  int i = 0;
  for(;i<len;i++)
  {
    arr_2[i] = 1;
  }

  for(i = 0;i<len;i++)
  {
    int j = 0;
    for(;j<=i;j++)
    {
      if(arr_1[j]< arr_1[i])
      {
        arr_2[i] = arr_2[j]+1;
      }
    }
  }
  int max = 0;
  for(i = 0;i<len;i++)
  {
    printf("%d ",arr_2[i]);
    if(arr_2[i]>max)
    {
      max = arr_2[i];
    }
  }
  printf("\n");
  return max;
}



int main()
{
  int arr_1[] = {3,6,1,4,2,8,9,5,7};
  int len = sizeof(arr_1)/sizeof(int);
  int *arr_2 = (int *)malloc(sizeof(int)*len);
  int res = fun(arr_1,arr_2,len);
  printf("res = %d\n",res);
  return 0;
}