第1周笔记5-Dijkstra最短路径问题

问题描述

        罗老师被邀请参加一个舞会，是在城市n，而罗老师当前所处的城市为1,附近还有很多城市2~n-1，有些城市之间没有直接相连的路，有些城市之间有直接相连的路，这些路都是双向的，当然也可能有多条。

        现在给出直接相邻城市的路长度，罗老师想知道从城市1到城市n，最短多少距离。

输入

        输入n, m，表示n个城市和m条路;

        接下来m行，每行a b c， 表示城市a与城市b有长度为c的路。

输出

        输出1到n的最短路。如果1到达不了n，就输出-1。

样例输入

5 5
1 2 20
2 3 30
3 4 20
4 5 20
1 5 100

样例输出

90

/** 单源最短路径，Dijkstra 算法，邻接矩阵形式，复杂度为O(n^2) 
* 求出源 beg 到所有点的最短路径，传入图的顶点数，和邻接矩阵 cost[][]
* 返回各点的最短路径 lowcost[], 路径 pre[].pre[i] 记录 beg 到 i 路径上的 父结点，pre[beg]=-1
* 可更改路径权类型，但是权值必须为非负 
*/

#include<iostream> 
using namespace std;

const int MAXN=2010;
#define typec int 
const typec INF=0x3f3f3f3f;
bool vis[MAXN];
int pre[MAXN];

int cost[MAXN][MAXN],lowcost[MAXN];
void Dijkstra(typec cost[][MAXN],typec lowcost[],int n,int beg){
	for(int i=0;i<n;i++){
		lowcost[i]=INF; vis[i]=false; pre[i]=-1; 
	}
	lowcost[beg]=0;
	for(int j=0;j<n;j++){
		int k=-1;
		int Min=INF;
		for(int i=0;i<n;i++){
			if(!vis[i]&&lowcost[i]<Min){
				Min=lowcost[i];
				k=i; 
			}
		}
		if(k==-1) break;
		vis[k]=true;
		for(int i=0;i<n;i++){
			if(!vis[i]&&lowcost[k]+cost[k][i]<lowcost[i]){
				lowcost[i]=lowcost[k]+cost[k][i];
				pre[i]=k;
			}
		}	
	}
}
int main(){
	int m,n;
	cin>>n>>m;
	for(int i=0;i<n;i++){
		for(int j=0;j<n;j++){
			if(i==j){
			cost[i][j]=0;
			}
			cost[i][j]=INF; 
		}
	}
	for(int i=0;i<m;i++){
		int x,y,w;
		cin>>x>>y>>w;
		cost[x-1][y-1]=w;
		cost[y-1][x-1]=w;
	}
	Dijkstra(cost,lowcost,n,0);
	if(lowcost[n-1]==INF){
		cout<<-1;
	}else{
		cout<<lowcost[n-1];
	}
	return 0;
}

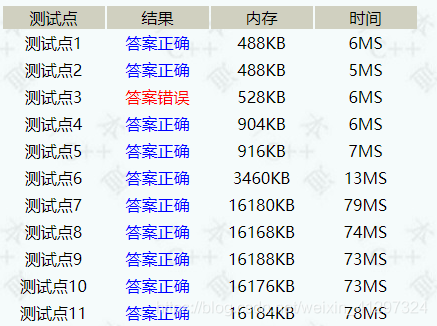
本人不才！有待提高！还有一个节点评测未通过，望大佬指点！

Dijkstra是什么？

        Dijkstra算法是指定一个源点，求得这个源点到各个点的最短路径。Dijkstra算法通过不断的松弛边，每次更新相邻点的路径，使之两点之间的距离成为最短的路径。Dijkstra算法缺点是不能有负权边的值。

        松弛边：点A到点B的距离是10，点A到点C的距离是15，点B到点C的距离是3，那么点A到点C的最短距离就是13。此时15这个值将会被废弃，永不使用，以后谈论点A到点C的距离都是直接说13。这就是松弛边。

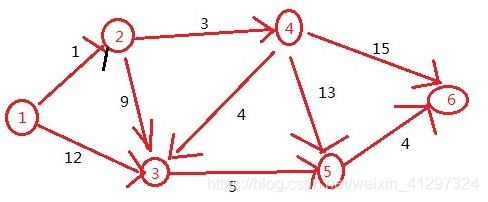
        现在有如下图，6个点，9条边，边是有方向的:

Dijkstra如何走？

假设源点为点(1):

1. 先求得源点到各个点的距离。则数组为dis['1'=>0, '2'=>1, '3'=>12, '4'=>'∞', '5'=>'∞', '6'=>'∞']；并且用数组e[i][j]表示点i到点j的距离。
2. 将各个点分为2个部分，P部分是已知的点1到该点距离为最短路径的点的集合，此时P部分只有点1到点1的距离为0是已知的，点1到点2，点1到点3的距离是不是最短路径暂时不可是，所以他们不属于这部分。Q部分是未知的点1到该点距离为最短路径的点的集合。
3. 在集合Q中选择一个点，这个点距离源点（1）号点最近，即步骤一得出的dis数组中该key所对应的值最小，此时这个点为2号点，因为dis[2]最小，为1。则点1到点2的距离dis[2]是最短的路径，已经已知了，所以将（2）号点加入到集合P中。此时以（2）好点为源点，对所有的边松弛一次，看看有没有一个点X，可以使得点1到点2再到点X的距离小于点1到点X的距离，如果有，则点1到点X的最短路径就是点1到点2再到点X的值。即如果dis[3] > dis[2] + e[2][x]，则dis[3] = dis[2] + e[2][x]。
4. 重复第三步，知道集合Q为空。