最小生成树&单源最短路径相关算法—Prim、Kruskal、Dijkstra——王道数据结构2025

生成树&最小生成树概念

生成树概念

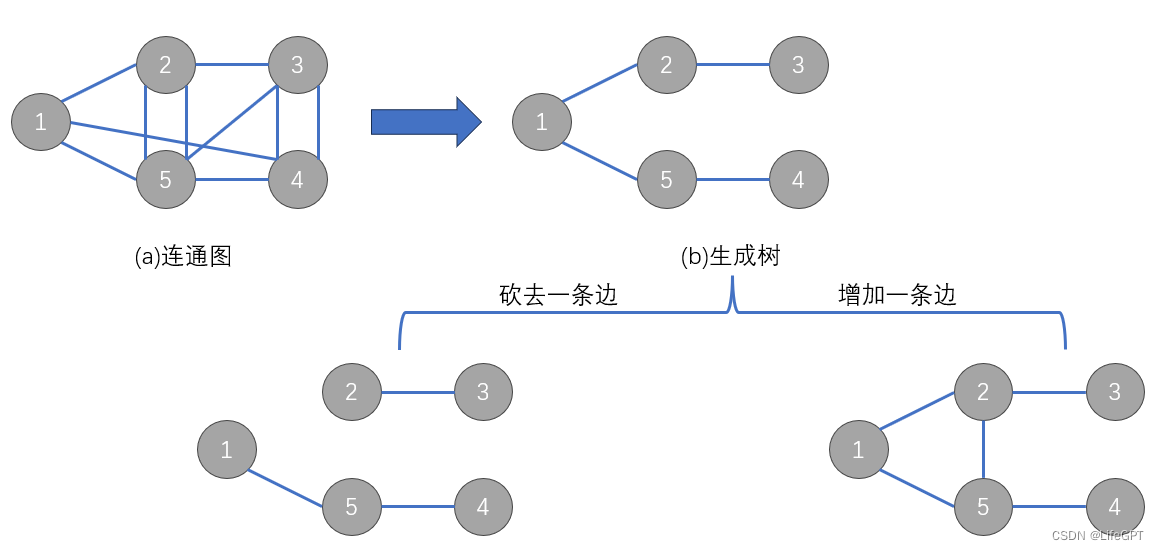
1、一个连通图的生成树包含原图的所有节点，并且只含尽可能少的边。

2、对于生成树：砍去一条边->非连通图；加一条边->形成一条回路。

最小生成树概念

1、一个带权连通无向图的可能形成的生成树中，权值和最小的那一颗生成树，即最小生成树；

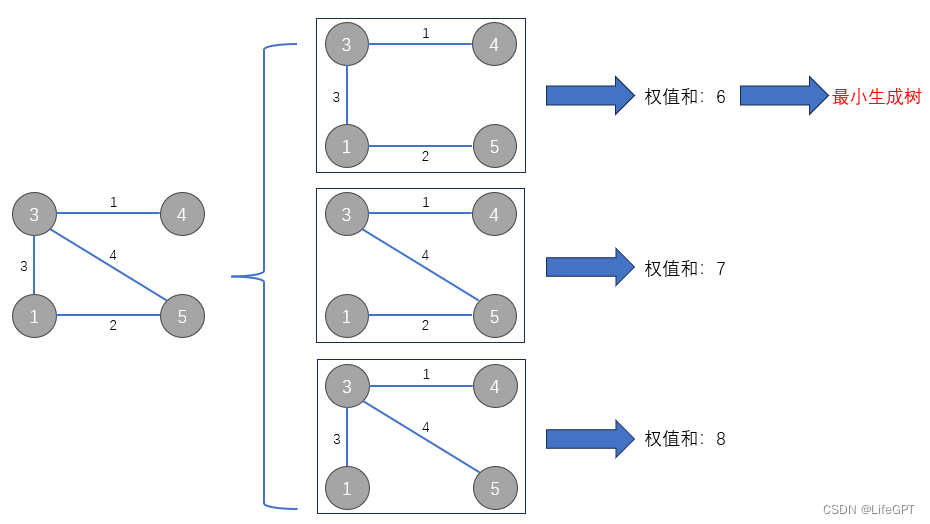
2、为什么是可能形成的生成树中选择出最小生成树？

因为一个图可以生成多种类型的树，例如：

最小生成树性质：

1、存在权值相同->最小生成树不唯一；权值都不同->最小生成树唯一；例如(权值3重复)：

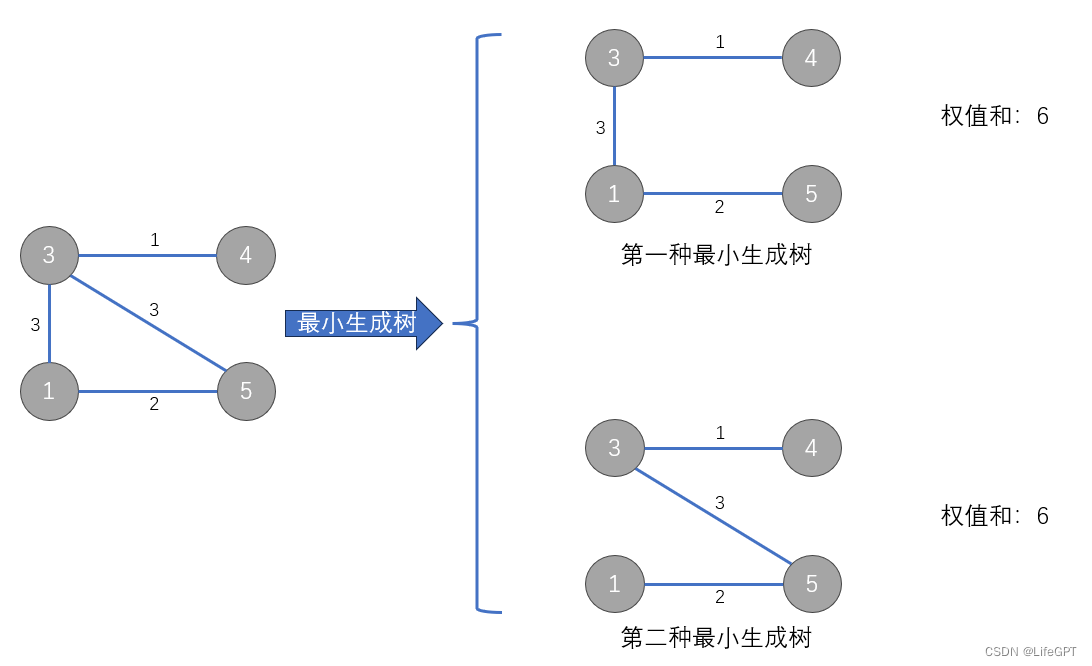
2、如上图，最小生成树即使不唯一，但每一颗的权值之和是唯一的，且都是最小的（之所以会发生最小生成树不唯一，是因为存在权值相同的边，此时可以选择保留一边，不同的选择会形成不同的树，但是这俩边的权值都是相同的，不论保留哪个都不影响最后的权值之和）

3、最小生成树的边数 E 等于顶点数 V - 1

构建最小生成树

基本性质

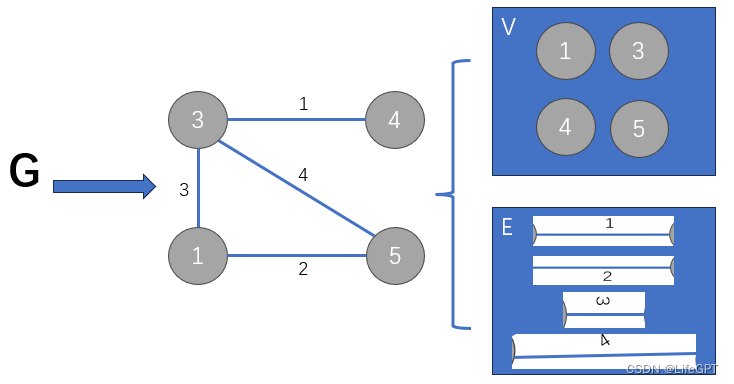
设带权连通无向图G = ( V , E ) ，其中：

G：代表带权连通无向图；        V：G 中的顶点集合：        E：G 中的边集合；

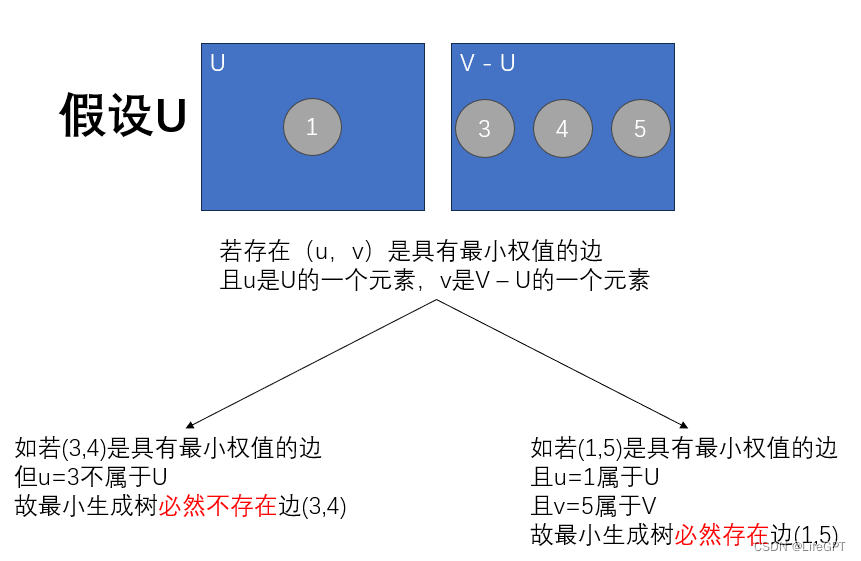
U 属于 V 的非空子集，u 是 U 中的元素，v 是 V - U中的元素；

若（u,v）是一条具有最小权值的边，则必存在一颗包含（u,v）的最小生成树；

看不懂？没事，我也看不懂：）......图解如下：