机器学习-逻辑回归

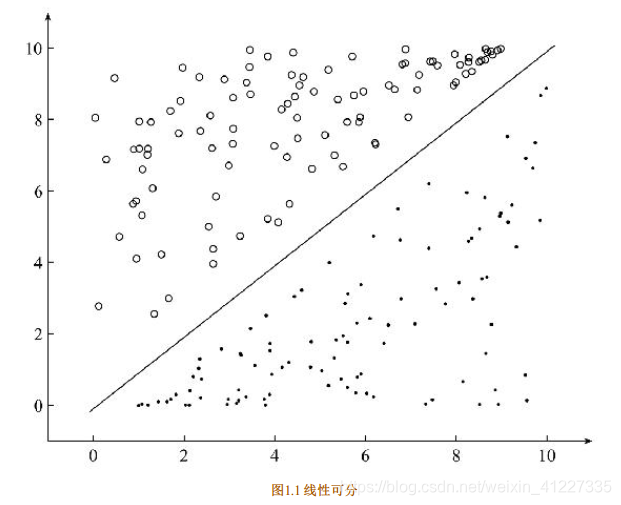
逻辑回归的原理：就是在一个平面里，找到一条直线将两个不同的类分开。
直线函数（直线也称为超平面）：
	Wx+b = 0

逻辑回归中，将这条直线（超平面）通过样本训练出来，即找出这条直线。	

如何将样本事先分好类进行训练？
	使用阈值函数分类，通常使用Sigmoid函数：

Sigmoid函数判断分类：
	对于输入向量X，它属于正例的概率：

	对于输入向量X，它是负例的概率：

这时候，输入向量X知道了，为样本X判断分类的Sigmoid函数也有了，
还差权重W和偏移量b如何求？

为了得到W和b，我们必须先使用极大似然估计来得到。
	而极大似然估计定义是什么？

那该如何使用这种极大似然法思想？
	1.先写出似然函数
	2.对似然函数取log
	3.求导数
	4.解似然方程

1.
然后：

2.这里的取对数，是取-log，这是NLL（the negative log likehood）。
得到损失函数小写l：

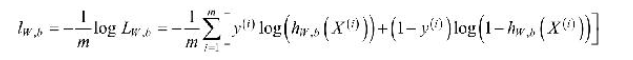
而我们需要得到损失函数的最小值：

3.如何求解损失函数最小值？

使用梯度下降法：

1.随机选择一个初始点w0
2.重复以下过程（这就是求导过程）：
  1.决定梯度下降的方向：
  2.选择步长α
  3.更新： wi+1 =wi +α · d i

3.直到满足终止条件
4.具体过程如下：

1.在初始时， 在点w0 处， 选择下降的方向d 0 ， 选择步长α ， 更新w的值
2.此时到达w1 处， 判断是否满足终止的条件， 发现并未到达最优解w∗  
3.重复上述的过程， 直至到达w∗ 。

这种梯度下降有两种优化：
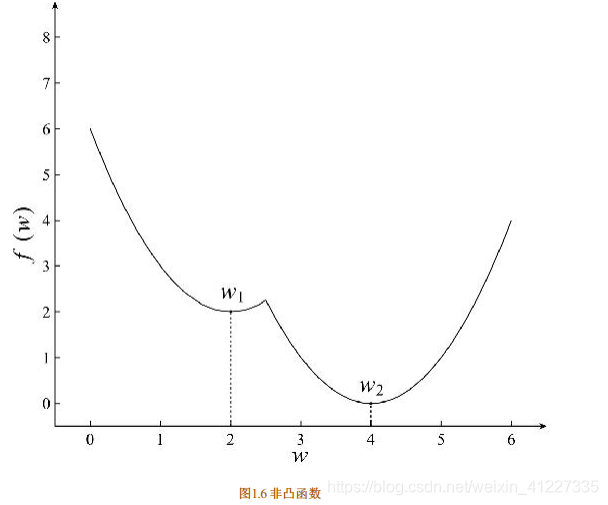
1.凸优化（凸函数）
2.非凸优化（非凸函数）

最小二乘（Least Squares） 、 
岭回归（Ridge Regression） 和
Logistic回归（Logistic Regression） 
的损失函数都是凸优化问题。

对于上述的Logistic Regression算法的损失函数可以通过梯度下降法对其进行求解， 
其梯度为：