今天我们来学习一个神奇的数据结构:Palindromic Tree。中译过来就是——回文树。
那么这个回文树有何功能?
假设我们有一个串S,S下标从0开始,则回文树能做到如下几点:
1.求串S前缀0~i内本质不同回文串的个数(两个串长度不同或者长度相同且至少有一个字符不同便是本质不同)
2.求串S内每一个本质不同回文串出现的次数
3.求串S内回文串的个数(其实就是1和2结合起来)
4.求以下标i结尾的回文串的个数
5.各种限制长度,求数目,限制数目,求长度
首先我们定义一些变量:
1.len[i]表示编号为i的节点表示的回文串的长度(一个节点表示一个回文串)
2.next[i][c]表示编号为i的节点表示的回文串在两边添加字符c以后变成的回文串的编号(和字典树类似)。
3.fail[i]表示节点i失配以后跳转不等于自身的节点i表示的回文串的最长后缀回文串(和AC自动机类似)。
4.cnt[i]表示节点i表示的本质不同的串的个数(建树时求出的不是完全的,最后count()函数跑一遍以后才是正确的)
5.num[i]表示以节点i表示的最长回文串的最右端点为回文串结尾的回文串个数。
6.last指向新添加一个字母后所形成的最长回文串表示的节点。
7.S[i]表示第i次添加的字符(一开始设S[0] = -1(可以是任意一个在串S中不会出现的字符))。
8.p表示添加的节点个数。
9.n表示添加的字符个数
其实可以说是两棵树,一棵是奇树、一棵是偶树。而回文树中
nex数组:指向的串为当前串两端加上同一个字符构成
nex算的后半段的子串加上一个字母,(偶)ab="baab" ab+c="cbaabc"
fail数组:fail跳转到自己这个串的最长回文后缀
例如:fail[aaaa]=aaa.
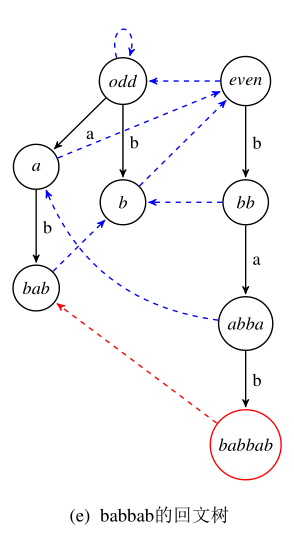
实线为nex指向节点。虚线为fail指向节点
用深搜搜索这棵树,遍历每个子串的情况
模板:搜索回文树并输出回文串
0位偶根,搜索到的为长度偶数的回文串
1位奇根,搜索到的为长度奇数的回文串
#include<bits/stdc++.h>
#define ll long long
#define sigma_size 30
#define MAXN 600005
using namespace std;
char pp[MAXN];
struct PAM{
int nex[MAXN][sigma_size]; //字符表的大小
int fail[MAXN];
int cnt[MAXN]; // 节点i表示的回文串在S中出现的次数(建树时求出的不是完全的,count()加上子节点以后才是正确的)
int num[MAXN]; //以节点i回文串的末尾字符结尾的但不包含本条路径上的回文串的数目。(也就是fail指针路径的深度)
int len[MAXN]; //节点i的回文串的长度 2~p-1()
int S[MAXN]; //表示第i次添加的字符 // 2~p-1
int last,n,p; //p-2是不同回文串个数
//last指向最新添加的回文结点
int newnode(int rt){//新建节点
memset(nex[p],0,sizeof(nex[p]));
cnt[p]=0;
num[p]=0;
len[p]=rt;
return p++;
}
void init(){//初始化
p=last=n=0;
newnode(0);
newnode(-1);
S[0]=-1;
fail[0]=1;
}
int getFail(int x){//寻找失败节点
while(S[n-len[x]-1]!=S[n]) x=fail[x];
return x;
}
void add(int c){ //插入字符,看题目要求
c=c-'a';
S[++n]=c;
int cur=getFail(last);
if(!nex[cur][c]){
int now=newnode(len[cur]+2);
fail[now]=nex[getFail(fail[cur])][c];
nex[cur][c]=now;
num[now]=num[fail[now]]+1;
}
last=nex[cur][c];
cnt[last]++;
}
void count1()//获得每个本质不同的回文子串的个数
{
for (int i = p-1; i >= 0; i--)
cnt[ fail[i] ] += cnt[i];
}
int ss[MAXN];
int tot=0;
void print(int sign)
{
for(int i=tot;i>=2;i--)
printf("%c",ss[i]+'a');
if(sign==0)
printf("%c",ss[1]+'a');
for(int i=1;i<=tot;i++)
printf("%c",ss[i]+'a');
printf("\n");
}
void dfs(int x,int sign)
{
for(int i=0;i<26;i++)
{
int v=nex[x][i];
if(v==0)
continue;
ss[++tot]=i;
print(sign);//打印本质不同回文子串
dfs(v,sign);
--tot;
}
}
void solve(char pp[])
{
init();
int len=strlen(pp+1);
for(int i=1;i<=len;i++)
add(pp[i]);
tot=0;
dfs(0,0);
tot=0;
dfs(1,1);
}
}pam;
int main()
{
pam.init();
scanf("%s",pp+1);
pam.solve(pp);
return 0;
}
1.求回文串的数目*长度的最大值
https://www.luogu.org/problem/P3649
题意:给你一个由小写拉丁字母组成的字符串 ss。我们定义 ss 的一个子串的存在值为这个子串在 ss 中出现的次数乘以这个子串的长度。
对于给你的这个字符串 ss,求所有回文子串中的最大存在值
解析:
直接贪心
ac:
#include<bits/stdc++.h>
#define ll long long
#define sigma_size 30
#define MAXN 600005
using namespace std;
char p[MAXN];
struct PAM{
int nex[MAXN][sigma_size]; //字符表的大小
int fail[MAXN];
int cnt[MAXN]; // 节点i表示的回文串在S中出现的次数(建树时求出的不是完全的,count()加上子节点以后才是正确的)
int num[MAXN]; //以节点i回文串的末尾字符结尾的但不包含本条路径上的回文串的数目。(也就是fail指针路径的深度)
int len[MAXN]; //节点i的回文串的长度 2~p-1
int S[MAXN]; //表示第i次添加的字符 // 2~p-1
int last,n,p; //p-2是不同回文串个数
//last指向最新添加的回文结点
int newnode(int rt){//新建节点
memset(nex[p],0,sizeof(nex[p]));
cnt[p]=0;
num[p]=0;
len[p]=rt;
return p++;
}
void init(){//初始化
p=last=n=0;
newnode(0);
newnode(-1);
S[0]=-1;
fail[0]=1;
}
int getFail(int x){//寻找失败节点
while(S[n-len[x]-1]!=S[n]) x=fail[x];
return x;
}
void add(int c){ //插入字符
//看题目要求
c=c-'a';
S[++n]=c;
int cur=getFail(last);
if(!nex[cur][c]){
int now=newnode(len[cur]+2);
fail[now]=nex[getFail(fail[cur])][c];
nex[cur][c]=now;
num[now]=num[fail[now]]+1;
}
last=nex[cur][c];
cnt[last]++;
}
void count1()//找最大的个数*长度
{
for (int i = p-1; i >= 0; i--)
cnt[ fail[i] ] += cnt[i];
}
ll solve()
{
count1();
ll ans=0;
for(int i=2;i<=p-1;i++)//遍历2~p-1,贪心出结果
ans=max(ans,1ll*cnt[i]*len[i]);
return ans;
}
}pam;
int main()
{
pam.init();
cin>>p;
int len=strlen(p);
for(int i=0;i<len;i++)
pam.add(p[i]);
cout<<pam.solve()<<endl;
return 0;
}
2.每个回文串不同字母数*每个回文串数目
https://nanti.jisuanke.com/t/41389
题意:
输出一个串的所以回文串子串的权值和,权值为子串的不同字母个数
例1:aba有:a,b,a,aba,权值分别为1,1,1,2
ac:
#include<bits/stdc++.h>
#define ll long long
#define sigma_size 30
#define MAXN 1200005
using namespace std;
char pp[MAXN];
struct PAM{
int nex[MAXN][sigma_size]; //字符表的大小
int fail[MAXN];
int cnt[MAXN]; // 节点i表示的回文串在S中出现的次数(建树时求出的不是完全的,count()加上子节点以后才是正确的)
int num[MAXN]; //以节点i回文串的末尾字符结尾的但不包含本条路径上的回文串的数目。(也就是fail指针路径的深度)
int len[MAXN]; //节点i的回文串的长度 2~p-1()
int S[MAXN]; //表示第i次添加的字符 // 2~p-1
int last,n,p; //p-2是不同回文串个数
//last指向最新添加的回文结点
int newnode(int rt){//新建节点
memset(nex[p],0,sizeof(nex[p]));
cnt[p]=0;
num[p]=0;
len[p]=rt;
return p++;
}
void init(){//初始化
p=last=n=0;
newnode(0);
newnode(-1);
S[0]=-1;
fail[0]=1;
}
int getFail(int x){//寻找失败节点
while(S[n-len[x]-1]!=S[n]) x=fail[x];
return x;
}
void add(int c){ //插入字符,看题目要求
c=c-'a';
S[++n]=c;
int cur=getFail(last);
if(!nex[cur][c]){
int now=newnode(len[cur]+2);
fail[now]=nex[getFail(fail[cur])][c];
nex[cur][c]=now;
num[now]=num[fail[now]]+1;
}
last=nex[cur][c];
cnt[last]++;
}
void getcnt()//获得每个本质不同的回文子串的个数
{
for (int i = p-1; i >= 0; i--)
cnt[ fail[i] ] += cnt[i];
}
int siz[30];//记录字符个数
ll ans=0;
void dfs(int x,ll cot)//遍历点,当前串不同字母个数
{
for(int i=0;i<26;i++)
{
int v=nex[x][i];
if(v==0)
continue;
if(siz[i]==0)//没有被标记过
{
siz[i]++;
ans+=((ll)cnt[v]*(cot+1));
dfs(v,cot+1);
siz[i]--;//回溯
}
else{//已经被标记
ans+=((ll)cnt[v]*cot);
dfs(v,cot);
}
}
}
void solve(char pp[])
{
init();
int gen=strlen(pp+1);
for(int i=1;i<=gen;i++)
add(pp[i]);
getcnt();
memset(siz,0,sizeof(siz));
dfs(0,0);//偶根
memset(siz,0,sizeof(siz));
dfs(1,0);//奇根
printf("%lld\n",ans);
}
}pam;
int main()
{
pam.init();
scanf("%s",pp+1);
pam.solve(pp);
return 0;
}
3.求有子串关系的回文串对数
https://ac.nowcoder.com/acm/contest/886/C
题意:
给定一个字符串,求该字符串的本质不同字符串集,有子串关系的字符串二元组的数目
例1:aba和a,b都是回文串,且a,b是aba的子串,ans=2
#include<bits/stdc++.h>
#define ll long long
#define sigma_size 30
#define MAXN 600005
using namespace std;
char pp[MAXN];
struct PAM{
int nex[MAXN][sigma_size]; //字符表的大小
int fail[MAXN];
int cnt[MAXN]; // 节点i表示的回文串在S中出现的次数(建树时求出的不是完全的,count()加上子节点以后才是正确的)
int num[MAXN]; //以节点i回文串的末尾字符结尾的但不包含本条路径上的回文串的数目。(也就是fail指针路径的深度)
int len[MAXN]; //节点i的回文串的长度 2~p-1()
int S[MAXN]; //表示第i次添加的字符 // 2~p-1
int last,n,p; //p-2是不同回文串个数
//last指向最新添加的回文结点
int newnode(int rt){//新建节点
memset(nex[p],0,sizeof(nex[p]));
cnt[p]=0;
num[p]=0;
len[p]=rt;
return p++;
}
void init(){//初始化
p=last=n=0;
newnode(0);
newnode(-1);
S[0]=-1;
fail[0]=1;
}
int getFail(int x){//寻找失败节点
while(S[n-len[x]-1]!=S[n]) x=fail[x];
return x;
}
void add(int c){ //插入字符,看题目要求
c=c-'a';
S[++n]=c;
int cur=getFail(last);
if(!nex[cur][c]){
int now=newnode(len[cur]+2);
fail[now]=nex[getFail(fail[cur])][c];
nex[cur][c]=now;
num[now]=num[fail[now]]+1;
}
last=nex[cur][c];
cnt[last]++;
}
void count1()//获得每个本质不同的回文子串的个数
{
for (int i = p-1; i >= 0; i--)
cnt[ fail[i] ] += cnt[i];
}
ll siz[MAXN],ant[MAXN];
int vis[MAXN];
void dfs(int x)
{
siz[x]=1;
ant[x]=(vis[x]==0)+(vis[fail[x]]==0);
vis[x]++,vis[fail[x]]++;
for(int i=0;i<26;i++)
{
int v=nex[x][i];
if(v==0)
continue;
dfs(v);
siz[x]+=siz[v];
}
vis[x]--,vis[fail[x]]--;
}
void solve(char pp[])
{
init();
int len=strlen(pp+1);
for(int i=1;i<=len;i++)
add(pp[i]);
dfs(1);
dfs(0);
ll ans=0;
for(int i=2;i<p;i++)
ans+=(siz[i]*ant[i]-1);
printf("%lld\n",ans);
}
}pam;
int main()
{
int t,cas=1;
scanf("%d",&t);
while(t--)
{
pam.init();
scanf("%s",pp+1);
printf("Case #%d: ",cas++);
pam.solve(pp);
}
return 0;
}
4.两个串相同回文子串对数
链接:https://vjudge.net/problem/Gym-100548G
题意:
给定2个串,求两个串相同回文子串的个数
解析:
建立两个回文树,同时搜索两颗回文树
对非根求 +cnt[x]*cnt[y],注意ll
代码:
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<algorithm>
#include<iostream>
#define ll long long
#define sigma_size 30
#define MAXN 600005
using namespace std;
struct PAM{
int nex[MAXN][sigma_size]; //字符表的大小
int fail[MAXN];
int cnt[MAXN]; // 节点i表示的回文串在S中出现的次数(建树时求出的不是完全的,count()加上子节点以后才是正确的)
int num[MAXN]; //以节点i回文串的末尾字符结尾的但不包含本条路径上的回文串的数目。(也就是fail指针路径的深度)
int len[MAXN]; //节点i的回文串的长度 2~p-1()
int S[MAXN]; //表示第i次添加的字符 // 2~p-1
int last,n,p; //p-2是不同回文串个数
//last指向最新添加的回文结点
int newnode(int rt){//新建节点
memset(nex[p],0,sizeof(nex[p]));
cnt[p]=0;
num[p]=0;
len[p]=rt;
return p++;
}
void init(){//初始化
p=last=n=0;
newnode(0);
newnode(-1);
S[0]=-1;
fail[0]=1;
}
int getFail(int x){//寻找失败节点
while(S[n-len[x]-1]!=S[n]) x=fail[x];
return x;
}
void add(int c){ //插入字符,看题目要求
c=c-'a';
S[++n]=c;
int cur=getFail(last);
if(!nex[cur][c]){
int now=newnode(len[cur]+2);
fail[now]=nex[getFail(fail[cur])][c];
nex[cur][c]=now;
num[now]=num[fail[now]]+1;
}
last=nex[cur][c];
cnt[last]++;
}
void count1()//获得每个本质不同的回文子串的个数
{
for (int i = p-1; i >= 0; i--)
cnt[ fail[i] ] += cnt[i];
}
void solve(char cc[])
{
init();
int len=strlen(cc+1);
for(int i=1;i<=len;i++)
add(cc[i]);
count1();
}
}AA,BB;
ll ans=0;
void dfs(int x,int y)//同时搜索两颗树,对非根累加结果,注意ll
{
if(x!=0&&y!=0&&x!=1&&y!=1){//非根,注意ll
ans+=1ll*AA.cnt[x]*BB.cnt[y];
}
for(int i=0;i<26;i++)
{
int a=AA.nex[x][i];
int b=BB.nex[y][i];
if(a==0||b==0)//要同时拥有才走
continue;
dfs(a,b);
}
}
char pp[MAXN];
char ss[MAXN];
int main()
{
int t,cas=1;
scanf("%d",&t);
while(t--)
{
scanf("%s",pp+1);
scanf("%s",ss+1);
AA.solve(pp);
BB.solve(ss);
ans=0;
dfs(1,1);
dfs(0,0);
printf("Case #%d: %lld\n",cas++,ans);
}
return 0;
}5.求折半还是回文串的个数
链接:http://acm.hdu.edu.cn/showproblem.php?pid=6599
解析:
fail[i]数组保存的是i回文串的最长后缀回文串,所以我们用fail数组反向建边,
从偶根出发跑一遍,标记,按要求记录答案即可,长度为1的要特殊处理
ac:
#include<bits/stdc++.h>
#define ll long long
#define sigma_size 30
#define MAXN 600005
using namespace std;
char p[MAXN];
vector<int> vc[300005];
struct PAM{
int nex[MAXN][sigma_size]; //字符表的大小
int fail[MAXN];
int cnt[MAXN]; // 节点i表示的回文串在S中出现的次数(建树时求出的不是完全的,count()加上子节点以后才是正确的)
int num[MAXN]; //以节点i回文串的末尾字符结尾的但不包含本条路径上的回文串的数目。(也就是fail指针路径的深度)
int len[MAXN]; //节点i的回文串的长度 2~p-1
int S[MAXN]; //表示第i次添加的字符 // 2~p-1
int last,n,p; //p-2是不同回文串个数
//last指向最新添加的回文结点
int vis[MAXN];
int sign[MAXN];
int newnode(int rt){//新建节点
memset(nex[p],0,sizeof(nex[p]));
cnt[p]=0;
num[p]=0;
len[p]=rt;
return p++;
}
void init(){//初始化
for(int i=0;i<=300000;i++)
vc[i].clear();
memset(vis,0,sizeof(vis));
memset(sign,0,sizeof(sign));
p=last=n=0;
newnode(0);
newnode(-1);
S[0]=-1;
fail[0]=1;
}
int getFail(int x){//寻找失败节点
while(S[n-len[x]-1]!=S[n]) x=fail[x];
return x;
}
void add(int c){ //插入字符
//看题目要求
c=c-'a';
S[++n]=c;
int cur=getFail(last);
if(!nex[cur][c]){
int now=newnode(len[cur]+2);
fail[now]=nex[getFail(fail[cur])][c];
nex[cur][c]=now;
num[now]=num[fail[now]]+1;
}
last=nex[cur][c];
cnt[last]++;
}
void count1()
{
for (int i = p-1; i >= 0; i--)
cnt[ fail[i] ] += cnt[i];
}
ll ans=0;
void dfs(int x)
{
if(len[x]==1)//1要特殊判断
sign[1]+=cnt[x];
else if(len[x]%2==1){
if(vis[len[x]/2+1])
sign[len[x]]+=cnt[x];
}
else if(len[x]!=0){
if(vis[len[x]/2])
sign[len[x]]+=cnt[x];
}
vis[len[x]]++;
for(int i=0;i<vc[x].size();i++)
dfs(vc[x][i]);
vis[len[x]]--;
}
void solve()
{
ans=0;
for(int i=2;i<=p-1;i++)//反向建边
vc[fail[i]].push_back(i);
count1();
dfs(0);
for(int i=1;i<n;i++)
printf("%d ",sign[i]);
printf("%d\n",sign[n]);
}
}pam;
int main()
{
pam.init();
while(scanf("%s",p)!=EOF)
{
int len=strlen(p);
for(int i=0;i<len;i++)
pam.add(p[i]);
pam.solve();
pam.init();
}
return 0;
}
























 538
538

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








