2.12 Python3 集合

集合是无序、不重复的元素集合，用大括号 {} 或 set() 函数创建。

---

目录

1. 创建集合

2. 集合的基本操作

成员检测

集合长度

遍历集合

集合运算

3. 集合内置方法

添加元素

移除元素

集合比较

复制集合

其他方法

4. Python 集合的主要作用

1. 快速成员检测

2. 去除重复元素

3. 数学集合运算

4. 高效数据比较

5. 关系数据库操作模拟

6. 过滤工具

7. 字典键的替代

---

1. 创建集合

# 创建空集合
empty_set = set()  # 注意: 不能用 {} 创建空集合，{} 创建的是空字典

# 创建有元素的集合
fruits = {'apple', 'banana', 'orange'}
numbers = {1, 2, 3, 4, 5}

# 从列表创建集合
colors = set(['red', 'green', 'blue', 'red'])  # 重复元素会被去除

# 从字符串创建集合
letters = set('hello')  # 结果为 {'h', 'e', 'l', 'o'}

print(fruits)  # 输出可能是 {'banana', 'orange', 'apple'} (顺序不固定)
print(colors)  # 输出 {'red', 'green', 'blue'}
print(letters) # 输出 {'h', 'e', 'l', 'o'}

---

2. 集合的基本操作

成员检测

fruits = {'apple', 'banana', 'orange'}
print('apple' in fruits)  # True
print('pear' not in fruits)  # True

集合长度

fruits = {'apple', 'banana', 'orange'}
print(len(fruits))  # 3

遍历集合

fruits = {'apple', 'banana', 'orange'}
for fruit in fruits:
    print(fruit)

集合运算

a = {1, 2, 3, 4}
b = {3, 4, 5, 6}

# 并集
print(a | b)  # {1, 2, 3, 4, 5, 6}
print(a.union(b))  # 同上

# 交集
print(a & b)  # {3, 4}
print(a.intersection(b))  # 同上

# 差集 (在a中但不在b中)
print(a - b)  # {1, 2}
print(a.difference(b))  # 同上

# 对称差集 (在a或b中，但不同时在两者中)
print(a ^ b)  # {1, 2, 5, 6}
print(a.symmetric_difference(b))  # 同上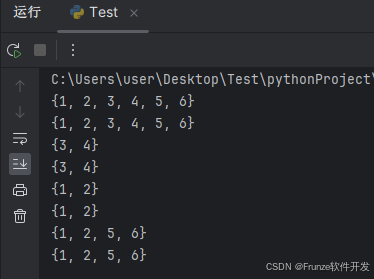

---

3. 集合内置方法

方法	描述
add()	为集合添加元素
clear()	移除集合中的所有元素
copy()	拷贝一个集合
difference()	返回多个集合的差集
difference_update()	移除集合中的元素，该元素在指定的集合也存在。
discard()	删除集合中指定的元素
intersection()	返回集合的交集
intersection_update()	返回集合的交集。
isdisjoint()	判断两个集合是否包含相同的元素，如果没有返回 True，否则返回 False。
issubset()	判断指定集合是否为该方法参数集合的子集。
issuperset()	判断该方法的参数集合是否为指定集合的子集
pop()	随机移除元素
remove()	移除指定元素
symmetric_difference()	返回两个集合中不重复的元素集合。
symmetric_difference_update()	移除当前集合中在另外一个指定集合相同的元素，并将另外一个指定集合中不同的元素插入到当前集合中。
union()	返回两个集合的并集
update()	给集合添加元素
len()	计算集合元素个数

添加元素

fruits.add('pear')  # 添加单个元素
fruits.update(['kiwi', 'mango'])  # 添加多个元素

移除元素

fruits.remove('banana')  # 移除元素，如果元素不存在会引发KeyError
fruits.discard('banana')  # 移除元素，如果元素不存在不会报错
popped = fruits.pop()  # 随机移除并返回一个元素
fruits.clear()  # 清空集合

集合比较

x = {1, 2, 3}
y = {1, 2}

print(y.issubset(x))  # True, y是x的子集
print(x.issuperset(y))  # True, x是y的超集
print(x.isdisjoint({5, 6}))  # True, 没有共同元素

复制集合

new_fruits = fruits.copy()  # 浅拷贝

其他方法

# 更新集合为与其他集合的交集
x.intersection_update(y)  # 等同于 x = x & y

# 更新集合为与其他集合的差集
x.difference_update(y)  # 等同于 x = x - y

# 更新集合为与其他集合的对称差集
x.symmetric_difference_update(y)  # 等同于 x = x ^ y

集合是Python中非常有用的数据结构，特别适合用于成员检测、去重和数学集合运算。由于集合基于哈希表实现，其成员检测操作的时间复杂度为O(1)，非常高效。

---

4. Python 集合的主要作用

集合(Set)是Python中一种非常有用的数据结构，它在编程中有多种重要用途：

1. 快速成员检测

集合基于哈希表实现，可以非常高效地检查元素是否存在：

words = {'apple', 'banana', 'orange'}
print('apple' in words)  # True - O(1)时间复杂度

比列表(list)的成员检测(O(n))快得多。

2. 去除重复元素

集合自动去除重复项，是去重的理想选择：

numbers = [1, 2, 2, 3, 4, 4, 5]
unique_numbers = set(numbers)  # {1, 2, 3, 4, 5}

3. 数学集合运算

集合支持丰富的数学集合操作：

A = {1, 2, 3}
B = {3, 4, 5}

# 并集
print(A | B)  # {1, 2, 3, 4, 5}

# 交集
print(A & B)  # {3}

# 差集
print(A - B)  # {1, 2}

# 对称差集
print(A ^ B)  # {1, 2, 4, 5}

4. 高效数据比较

可以快速比较两组数据的差异：

old_users = {'Alice', 'Bob', 'Charlie'}
new_users = {'Bob', 'David', 'Eve'}

# 新增用户
print(new_users - old_users)  # {'David', 'Eve'}

# 流失用户
print(old_users - new_users)  # {'Alice', 'Charlie'}

5. 关系数据库操作模拟

可以模拟SQL中的JOIN操作：

customers = {'Alice', 'Bob', 'Charlie'}
purchased = {'Bob', 'David'}

# 已购买客户(内连接)
print(customers & purchased)  # {'Bob'}

# 未购买客户(左外连接差异)
print(customers - purchased)  # {'Alice', 'Charlie'}

6. 过滤工具

可以快速过滤数据：

valid_tags = {'python', 'java', 'javascript'}
user_tags = {'python', 'c++', 'ruby'}

# 找出有效的用户标签
print(user_tags & valid_tags)  # {'python'}

7. 字典键的替代

当只需要键而不需要值时，集合比字典更合适：

# 用集合代替只有键的字典
present_students = {'Alice', 'Bob'}  # 比 {'Alice': True, 'Bob': True} 更高效

---

集合的这些特性使其成为处理唯一性数据、快速查找和集合运算时的理想选择。

---