机器学习算法之SVM（一）初识

首先，面对下图所示的分类问题

                                

我们用一条直线就可以将其很好的分开

                         

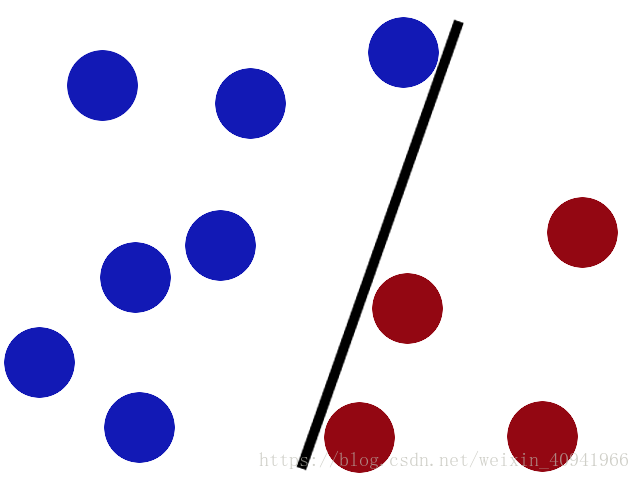
但是，当面对线性不可分的情况该怎么处理呢？当然我们可以说用曲线方程，但是这个曲线方程怎么去求解却是个大问题。

                               

有人就提出了将其映射到高维空间中，利用一个平面将其线性划分为两类

   

然后，再投射回低维

 

在SVM中，划分的平面就叫做超平面（Hyperplane）；在高维的空间中我们确是能进行线性划分，但是随着维度的升高，计算量会巨大，于是就引入了核函数（Kernal Function）来解决这个问题；另外，我们在用平面进行划分时，追求让该平面到两侧最近点的距离（称为Margin）保持最大化，并称这些点（空间中用向量表示）为支持向量（Support Vector）。

Youtube上看到的算法实现的可视化过程，地址：https://youtu.be/3liCbRZPrZA

本人也是初学，如有理解不对的还望指正！