信号和随机过程

一、信号：信号是消息或信息的载体，通信的过程实质上是对信号处理、变换和传递的过程。通信中的信号可以分为两大类：确知信号和随机信号。随机信号和噪声都是随机变化或不可预测的，它们统称为随机过程。

(1)、确知信号：确知信号是可以预先确知其变化规律的信号。它在定义域的任意时刻都有确定的函数值，因而可用明确的数学表达式或波形来表示。

(2)、随机信号：是在定义域内的任意时刻都没有确定的函数值。例如：通信系统中的接收信号、热噪声等。

---

二、随机过程：通信中的信号和噪声都具有一定的随机性，需要用随机过程的理论来描述。随机过程可以定义为所有样本函数的集合。在某次观测中，观察到的只是随机过程中的一个样本，至于是哪一个样本，在观测之前是无法预见的，这正是随机过程随机性的表现。随机过程还可以定义为在时间进程中处于不同时刻的随机变量的集合。

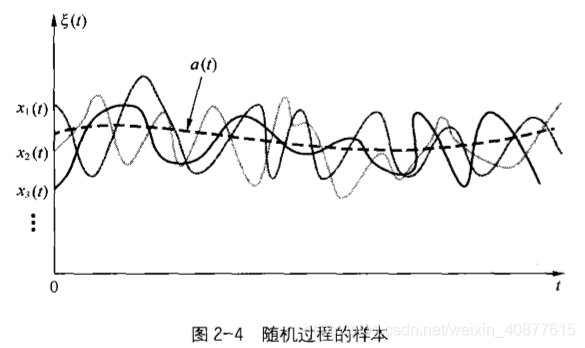
随机过程的数字特征：均值、方差、相关函数。

(1)、平稳随机过程：若随机过程的统计特性不随时间的推移而改变，那么该随机过程是严(格)平稳的；若随机过程的均值与t无关，而自相关函数仅与时间间隔有关，那么该随机过程是宽(广义)平稳的。严平稳必然是宽平稳的，反之不一定。通信系统中的信号与噪声大多可视为宽平稳过程。

(2)、高斯随机过程：通信系统中的热噪声等都是高斯型的，常称为高斯噪声。若高斯过程是宽平稳的，则也是严平稳的。

(3)、窄带随机过程：