2022.06.06-2022.06.12

2022-06-06

  评价一种防御方法的防御能力需要考虑适应性攻击方式。适应性攻击是指攻击者对提出的防御机制又一定的了解，针对防御机制设计的攻击方法。论文中假设了两种不同强度的适应性攻击者：（1）skilled adversaries：了解到目标模型有trapdoor防御机制，但是不清楚具体的细节。（2）oracle adversaries：知道trapdoor的所有细节，包括他们的形状、位置和强度。

Trapdoor Detection and Removal

Skilled Adversary
  第一种攻击方法是使用去除后门的方法将trapdoor从模型中移除或检测出来，因为trapdoor的原理和注入后门是类似的。
  去除后门的方法包括裁剪多余的神经元，但是之前的工作表明，当剪枝冗余神经元时，正常模型精度迅速下降。此外，裁剪的方法也改变了新的模型的决策边界与原始模型的决策边界。因此，欺骗修剪后的模型的对抗性例子不能很好地转移到原始模型上，因为对抗性攻击只在具有类似决策边界的模型之间转移。
  论文在修剪过的单标签防御MNIST、GTSRB、CIFAR10和YouTubeFace模型上对六种不同的攻击进行了经验验证了这一点。我们建议来修剪神经元。然而，我们观察到，模型的正常精度在修剪时迅速下降（下降了 32.23%）。由于剪枝模型与原始模型之间存在显著差异，在剪枝模型上制作的对抗性样本不会转移到原始的trapdoor模型中。攻击的成功率 <4.67%。
  第二种攻击方式是黑盒攻击的方法。黑箱攻击必须严格避开trapdoor。为了生成成功转移到${\mathcal{F}}_{\theta }$的对抗示例，攻击者必须使用靠近分类化边界的输入重复查询${\mathcal{F}}_{\theta }$。然而，这样做意味着黑盒攻击也可以将${\mathcal{F}}_{\theta }$的活板门导入到替代模型中。替代模型确实继承了${\mathcal{F}}_{\theta }$的活板门。

Oracle Adversary
  第一种攻击方法是使用后门解锁技术创建了每个陷阱模型的新版本，它将活板门注入的成功率从99%降低到可以忽略不计的比率（约 2%）。不出所料，活板门防御无法检测到在清洁模型Fθ上构建的敌对样本，在 5% 的FPR下，GTSRB的检测成功率只有 7.42%。然而，这些未被检测到的对抗性样本并没有转移到trapdoor模型${\mathcal{F}}_{\theta }$中。对于所有六种攻击和所有四种模型，在${\mathcal{F}}_{\theta }$上的攻击成功率在 0% 到 6.7% 之间。我们假设，这可能是因为一个trapdoor模型${\mathcal{F}}_{\theta }$学习到了${\mathcal{F}}_{\theta }^{unlearn}$不知道的独特的 trapdoor 分布。这种分布转移导致了显著的差异，足以防止对立的例子在模型之间转移。

  第二种攻击方法，作者考虑了最强的攻击者：oracle攻击者以某种方式获得了访问（或完全复制）原始的干净模型。使用原始的干净模型来生成对抗样本。作者惊讶地发现，添加trapdoor已经在原始的清洁模型中引入了重大的变化，从而破坏了它们之间的对抗性攻击的可转移性。在表5中，我们展示了从干净模型到传统的对应模型的可转移性。对于所有6种攻击和所有模型，可转移性总是永远不会超过3%。这个明确的结果表明，无论攻击者在清除或取消活板门方面多么成功，或者如果他们重建原始模型，他们的努力都将失败，因为来自这些模型的对抗性例子不能在实际攻击目标的陷阱模型${\mathcal{F}}_{\theta }$上工作。

Advanced Adaptive Attacks (Carlini)

由Carlini与作者合作提出的两种适应性攻击能有效突破trapdoor模型的检测机制。两种攻击方法有两个共同的一般原则。首先，他们使用不同的技术来映射出存在于受保护模型中的trapdoor的边界，即它们的检测特征$g(x)$，然后设计方法来计算避免它们的对抗性扰动。其次，它们利用了显著的计算能力，远远超过了正常的实验水平，例如，运行10K的优化迭代，而不是在收敛时终止。我们认为这些对于攻击者来说是相当合理的，并且不考虑将计算开销作为一个减轻问题的因素。
  第一种攻击方法使用了Oracle攻击者的假设，即攻击者知道活板门的精确值。结合对模型的白盒访问，攻击者因此能够为模型中的任何一层生成与活板门的输入相匹配的神经元值。然后，攻击者在搜索敌对的例子时，联合优化与已知的活板门签名的最大余弦距离。
       
第二种攻击方法，称之为Trapdoor Vault Attack，并不需要知道活板门的签名。相反，它从计算多个输入图像上计算敌对例子的结果来估计活板门签名。文中通过使用直方图/聚类方法来近似每个N个活板门的神经元特征，从而进一步推断为针对多个活板门。然后，攻击者计算联合优化，最大化到已知的活板门签名的距离，同时搜索敌对的例子。我们再次假设攻击者知道模型中存在的活板门的确切数量。

2022-06-13

Evading Adversarial Example Detection Defenses with Orthogonal Projected Gradient Descent

符号系统定义
分类模型 $f:{\mathbb{R}}^d\to {\mathbb{R}}^n$ ，输入 $x\in {\mathbb{R}}^d$，输出 $f(x)\in {\mathbb{R}}^n$.
检测约束：$g:{\mathbb{R}}^d\to \mathbb{R}$，$g(x)<0$ 满足条件，$g(x)>0$ 不满足条件.
真实标签：$c(x)=y$.
损失函数：$\mathcal{L}$.
嵌入向量：$e(x)$ 表示输入 $x$ 在 $f$ 的中间层上的嵌入。除非另有指定，否则 $e$返回紧邻 softmax 激活之前的 logit 向量.

使用投影梯度法生成对抗样本
  梯度投影法的基本思想：当迭代点 $x_k$ 是可行域 $\mathcal{D}$ 的内点时，取 $d=-\nabla f(x_k)$ 作为搜索方向；否则，当$x_k$ 是可行域 $\mathcal{D}$ 的边界点时，取 $-\nabla f(x_k)$ 这些边界面交集上的投影作为搜索方向。
  给定损失函数 $\mathcal{L}(f,x,t)$,输入参数分别是分类模型，训练样本，目标标签。给定约束条件 S ϵ = { z : d ( x , z ) < ϵ } S_\epsilon = \{z:d(x,z)<\epsilon\} Sϵ​={z:d(x,z)<ϵ}，优化目标定义为
$$x^{\prime }=\underset{z\in S_{ϵ}}{\mathrm{argmin}}\mathcal{L}(f,z,t)$$
迭代步骤定义为
$$x_{i+1}=P_{S_{ϵ}}(x_i-\alpha {\nabla }_{x_i}\mathcal{L}(f,z,t))$$
其中 $P_{S_{ϵ}}(z)$ 表示 $z$ 在 $S_{ϵ}$ 上的投影。例如，投影 $P_{S_{ϵ}}(z)$ 在约束 $d(x,z)=\Vert x-z{\Vert }_{\infty }$ 下是通过把 $z$ 裁剪到 $[x-ϵ,x+ϵ]$。

选择性梯度下降
  现有的用于对抗神经网络的检测策略的方法定义如下
$$\underset{x\in S_{ϵ}}{\mathrm{argmin}}\mathcal{L}(f,x,t)+\lambda g(x)$$
其中，$\lambda$ 是一个超参数，它控制着欺骗分类器和欺骗检测器的相对重要性。
  不同于上面的方式，文中没有最小化 $f$ 和 $g$ 的加权和，而是采用分步优化的方式，其攻击方法定义如下
$$\mathcal{A}(x,t)=\underset{x^{\prime }:\Vert x-x^{\prime }\Vert <ϵ}{\mathrm{argmin}}\underset{{\mathcal{L}}_{\mathrm{u}\mathrm{p}\mathrm{d}\mathrm{a}\mathrm{t}\mathrm{e}}(x,t)}{\underbrace{\mathcal{L}(f,x^{\prime },t)\cdot \mathbb{I}(f(x)\ne t)+g(x^{\prime })\cdot \mathbb{I}(f(x)=t)}}$$
  这里的想法是，我们不是最小化两个损失函数的凸组合，而是根据 $f(x)=t$ 是否成立选择性地优化 $f$ 或 $g$，确保更新总是有助于改善 $f$ 的损失或 $g$ 的损失。
  这种优化方式的另一个好处是，它将梯度下降步骤分解为两个更新，这防止了梯度不平衡问题：其中两个损失函数的梯度大小不相同，将导致优化过程不稳定。上面的公式可以简化为如下的形式
$$\nabla {\mathcal{L}}_{\mathrm{u}\mathrm{p}\mathrm{d}\mathrm{a}\mathrm{t}\mathrm{e}}(x,t)=\{\begin{array}{ll}\nabla \mathcal{L}(f,x,t)& \text{if f(x)=t,}\\ \nabla g(x)& \text{if f(x)=t.}\end{array}$$
正交梯度下降
上面的攻击方法在数学上是正确的，但是可能会遇到数值不稳定的困难。通常，$f$ 和 $g$ 的梯度指向相反的方向，因此，花费在优化 $f$ 上的每一步都会导致对 $g$ 进行优化的倒退。这将导致优化器在执行的每一步之后都不断地“撤消”它自己的进度。我们通过给出一个稍微不同的更新规则来解决这个问题，更新上面的公式如下
$$\nabla {\mathcal{L}}_{\mathrm{u}\mathrm{p}\mathrm{d}\mathrm{a}\mathrm{t}\mathrm{e}}(x,t)=\{\begin{array}{ll}\nabla \mathcal{L}(f,x,t)-{\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{j}}_{\nabla \mathcal{L}(f,x,t)}\nabla g(x)& \text{if f(x)=t,}\\ \nabla g(x)-{\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{j}}_{\nabla g(x)}\nabla \mathcal{L}(f,x,t)& \text{if f(x)=t.}\end{array}$$
其中 ${\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{j}}_{\nabla \mathcal{L}(f,x,t)}\nabla g(x)$ 表示梯度 $\nabla \mathcal{L}(f,x,t)$ 在 $\nabla g(x)$ 上的投影，${\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{j}}_{\nabla g(x)}\nabla \mathcal{L}(f,x,t)$ 同理。这里使用到了数学上的施密特正交化，下面简单解释以下：
  假设有两个线性无关的向量 $a$ 和 $b$, 现在要将两个向量正交化。首先是保持 $a$ 不动，让 $a=A$, 接下来寻找另一个向量 $B$, 使得 $A\perp B$。如下图，$p$ 是 $b$ 在 $a$ 上的投影，$B$ 就相当于 $b$ 的误差向量：

通过公式计算$x$，$x$ 是一个标量
$$x=\frac{a^{\top }b}{a^{\top }a}$$
$$p=ax=xa=\frac{a^{\top }b}{a^{\top }a}a$$
$$B=b-p$$
结合公式中 ${\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{j}}_{\nabla \mathcal{L}(f,x,t)}\nabla g(x)$ 就表示 $p$，$\nabla \mathcal{L}(f,x,t)-{\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{j}}_{\nabla \mathcal{L}(f,x,t)}\nabla g(x)$ 就表示 $B$

2022-06-13

Attack as Defense: Characterizing Adversarial Examples using Robustness

  一个通常的基本假设是，对抗性和良性的例子在特定的子空间分布上有所不同, 基于此有很多的检测方法，例如从 核密度，局部内在维度等方法，虽然这些特征提供了一些关于对抗性子空间的见解，但它们远不能可靠地单独区分对抗性的例子。更糟糕的是，攻击者可以通过专门设计的自适应攻击，轻松地破坏现有的防御机制。
  在这项工作中，我们提出了一个新的特征，即鲁棒性，以区分对抗性的例子和良性的例子。我们的主要观察结果是，对抗性的例子（由大多数现有的攻击方法制作）的可靠性明显不如良性的例子。
  不同于先前提出的特征，样本在鲁棒性上的差异来自于模型训练和对抗性实例生成的两个固有特征。首先，模型训练逐步最小化每个例子相对于模型的损失。因此，一个良性的例子经常被训练成对一个具有良好泛化的模型具有鲁棒性。因此，良性的例子通常相对远离决策边界。其次，大多数对抗性攻击的目的是产生人类难以察觉的扰动，这往往会产生不那么健壮的仅跨决策边界的对抗性例子。对比鲜明的鲁棒性特征使它适合于区分对抗性的例子和良性的例子。

  为了量化正常样本和对抗样本的鲁棒性，作者采用了 “CLAVER” 分数作为评分标准

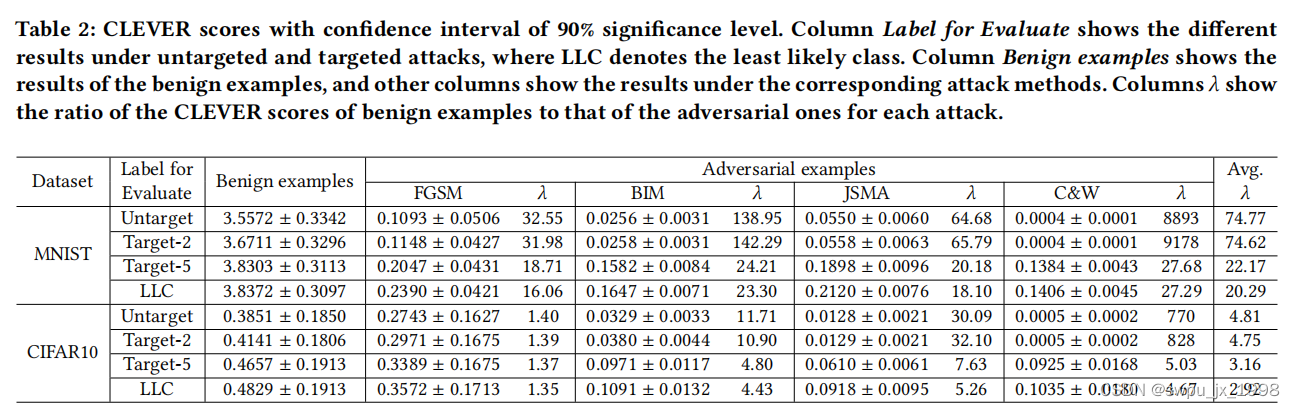
  从表中可以观察到，对于MNIST和CIFAR10数据集，良性例子的聪明分数比对抗例子的分数大得多，尽管攻击和数据集不同。这表明对抗性和良性例子之间的鲁棒性差异是显著的，从而证实了我们的观察。我们还观察到，使用非目标/目标-2标签来计算聪明分数的𝜆比率比使用其他标签的𝜆比率要大。这是因为每个敌对例子的非目标或目标-2标签通常是其良性对应的标签，这也证实了我们的观察，即每个敌对例子的𝜖邻域的大多数例子都有相同的良性对应标签。
  虽然使用 “CLAVER” 评分可以很好的判断样本的鲁棒性，但是其计算成本太高了，不适用于大型的模型。因此，作者提出了一种新的度量鲁棒性的方式：用攻击成本来测试样本的鲁棒性。基本的假设是，这个样本越健壮，攻击就越困难（攻击成本就越大）。这意味着我们可以通过使用现成的攻击来决定一个输入示例是否可能是敌对性的。
  使用攻击成本来评判健壮性需要解决两个问题。第一个问题是选择什么样的攻击方法。通常选择的攻击方法能够被量化而且能反映出样本的健壮性。因此，FGSM这种攻击方法就不合适，因为这种方法只进行一次的迭代步骤就结束了。相反，像 BIM， JSMA，C&W 这些迭代攻击方法就很合适。作者实验证明了其提出的方法的真确性

“CLEVER” 分数越高，其攻击需要的时间就越久
  第二个问题是如何描述不同类型的攻击的攻击成本。因为攻击时间受硬件设备影响，所以攻击时间不适和。对于一个迭代的攻击方式，其迭代次数和攻击时间是相关的，可以用来作为攻击成本的指标。

  为了证明攻击成本对表征对抗样本的有效性，我们选择了 5 种类型的图像（Benign、FGSM、BIM、DeepFool 和 C&W），每种图像随机选择 1,000 个样本，并将每种类型的图像分成两个独立的集合。然后我们使用 JSMA 攻击这些图像并记录所需的迭代次数。为了显示攻击成本的差异，我们计算了每对示例集之间迭代次数的平均欧几里德距离，结果如图所示。我们可以看到，对于不同类型的示例（对抗性与良性） ，距离很远。而对于相同类型的示例（对抗性与对抗性或良性与良性），距离接近于零。值得一提的是，对于不同攻击生成的样本，距离也非常相似，这意味着即使对抗样本是由不同攻击生成的，它们也是“同源”样本，具有相似的攻击成本。

检测方法

K-NN Based Detection Approach

假设有两个不相交的集合 $A$ 和 $B$, $B$ 是正常样本的集合，$A$ 是对抗样本的集合
Single detector
对于集合 $A\cup B$ 中的每一个样本，使用上面的方法计算出攻击代价 ${\alpha }_y$, 可以得到一个集合 D = { α y ∣ y ∈ A ∪ B } D = \{\alpha_y|y \in A\cup B\} D={αy​∣y∈A∪B}。对于一个未知的输入 $x$ 以及参数 $K$，我们首先计算攻击代价 ${\alpha }_x$。然后从集合 $D$ 中选择 $K$ 个与 ${\alpha }_x$ 最近的值得到集合 N K = { α y i ∣ 1 ≤   i ≤ K } N_K=\{\alpha_{y_i} | 1\leq\ i \leq K \} NK​={αyi​​∣1≤ i≤K}。计算 $N_K$ 中属于 $A$ 的个数 $A_x$ 和属于 $B$ 的个数 $B_x$，如果 $A_x\ge B_x$，则 $x$ 分类为对抗样本。

Ensembele detector
上面的单标签检测使用一种对抗攻击方法来生成 $D$，而多标签检测则使用多种对抗攻击的方法来生成攻击成本。则 ${\alpha }_y$ 从一个值变成了一个向量 ${\overrightarrow{\alpha }}_y=({\alpha }_y^1,\cdots ,{\alpha }_y^n)$，每一个维度都代表一种不同的攻击方式。同样可以得到集合 D = { α → y ∣ y ∈ A ∪ B } D = \{\overrightarrow{\alpha}_y|y \in A\cup B\} D={α y​∣y∈A∪B}。同样与 “single detector” 检测类似，使用 $k$-$NN$ 的方法检测。

Z-Score Based Detection Approach

Z-score 是统计学中一个众所周知的概念，用于测量样本与数据集的平均值和标准差的关系。一个样本 $i$ 的 Z-score 定义为：$z=\frac{i-\mu }{\sigma }$，$\mu$ 是样本均值，$\sigma$ 是样本的标准差。
Single detector
正常样本的集合 $B$ , 假设其样本的分布是近似正态分布 $N(\mu ,{\sigma }^2)$。否则，我们可以通过应用Box-Cox功率变换来对其进行变换。运用一种攻击方式计算出 $B$ 中样本的攻击成本 ${\alpha }_y$ 。因此，一个样本 $y$ 的 Z-score 分数 $z_y$ 定义为：$z_y=\frac{{\alpha }_y-\mu }{\sigma }$。给定一个标准差的比值 $h$ 作为阈值，如果 一个未知的样本 $x$ , 计算得到其 $z_x<h$，则 样本$x$ 分类为对抗样本。

Ensemble detector
同single detector 相似，运用多种攻击方法来进行防御，就会得到一个样本的多个攻击方法下的 Z-score，假设有 $n$ 个结果，如果其中 $k$ 个结果都判断未知样本为对抗样本，则最终结果也为对抗样本。

2022-06-18

Feature-Indistinguishable Attack to Circumvent Trapdoor-Enabled Defense

Basic Scheme

Optimization Problem： 目标类别的集合 $C_t$，输入样本 $x\in \mathcal{X}$，并且 $x\notin C_t$，${\mathcal{D}}_t$ 是 $C_t$ 在模型的 $L$ 层的输出特征的分布，叫做 $generation$ $layer$，${\mathcal{F}}_L(x)$ 表示模型在选择的 $L$ 层的输出，FIA 的基本策略是最小化对抗样本的潜在特征 ${\mathcal{F}}_L(x+ϵ)$ 和目标样本的 ${\mathcal{F}}_L^{tgt}\in {\mathcal{D}}_t$ 的距离，定义如下：
$$\begin{gathered} \underset{ϵ}{\min }\mathbf{D}({\mathcal{F}}_L(x+ϵ),{\mathcal{F}}_L^{tgt}), \\ \mathrm{s}.\mathrm{t}.{\mathcal{F}}_{\mathrm{L}}(\mathrm{x}+ϵ)\in {\mathcal{D}}_{\mathrm{t}} \end{gathered}$$
其中 $\mathbf{D}$ 是距离函数。上面式子的约束条件确保生成的对抗样本和良性的目标样本是不可区分。
  FIA在公式中使用了两个距离损失函数，并且同时最小化这两个距离。一个是 $L_2$ 的距离。它的目标是将敌对的例子引入目标类别 $C_t$。另一个是与目标的余弦相似度。它的目标是确保一个对抗性的例子有一个类似于目标表示方向的特征向量，依赖于特征空间中与活板门签名的余弦相似性来检测的陷门防御模型，不太可能检测到它。最优化问题将变成：
min ⁡ ϵ { − c o s ( F L ( x + ϵ ) , F L t g t ) + λ ⋅ ∥ F L ( x + ϵ ) − F L t g t ∥ 2 } , s . t . F L ( x + ϵ ) ∈ D t \min_\epsilon\{-cos(\mathcal{F}_L(x+\epsilon),\mathcal{F}_L^{tgt})+\lambda \cdot \| \mathcal{F}_L(x+\epsilon)-\mathcal{F}_L^{tgt} \|_2\},\\ \rm{s.t.} \mathcal{F}_L(x+\epsilon) \in \mathcal{D}_t ϵmin​{−cos(FL​(x+ϵ),FLtgt​)+λ⋅∥FL​(x+ϵ)−FLtgt​∥2​},s.t.FL​(x+ϵ)∈Dt​

Basic Scheme： 为了确保方程式中的约束条件。我们需要估计目标类别 $C_t$ 的特征表示分布 ${\mathcal{D}}_t$。 FIA 采用了一种不太准确但简单的方法：我们假设目标类别 $C_t$ 中良性示例的特征表示可以形成一个凸区域. 有了这个假设，我们可以选择良性示例的特征表示的期望作为目标表示
$${\mathcal{F}}_L^{tgt}={\mathcal{F}}_L^{C_t}={\mathbf{E}}_{x\in C_t}{\mathcal{F}}_L(x)$$
其中 $\mathbf{E}(\cdot )$ 是期望函数，使用良性样本的 ${\mathcal{F}}_L^{C_t}$ 特征的余弦相似度分布作为 ${\mathcal{D}}_t$ 的近视分布。
  由于期望对离群值很敏感，所以我们在计算等式中的期望之前，使用 DBSCAN 来确定并去除离群值 : 位于特征空间中最低密度区域的良性目标样本的一定比例（在我们的评估中为10%）被视为异常值并去除。然后，我们计算一个阈值 $c_p$，即期望和存活的良性目标样本之间的最小余弦相似度。我们要求一个对抗性例子的代表特征与期望 ${\mathcal{F}}_L^{C_t}$ 的余弦相似度在 $c_p$ 范围内。
min ⁡ ϵ { − c o s ( F L ( x + ϵ ) , F L C t ) + λ ⋅ ∥ F L ( x + ϵ ) − F L C t ∥ 2 } , s . t . c o s ( F L ( x + ϵ ) , F L C t ) ≥ c p \min_\epsilon\{-cos(\mathcal{F}_L(x+\epsilon),\mathcal{F}_L^{C_t})+\lambda \cdot \| \mathcal{F}_L(x+\epsilon)-\mathcal{F}_L^{C_t} \|_2\},\\ \rm{s.t.} cos(\mathcal{F}_{\it{L}}(\it{x+\epsilon}), \mathcal{F}_L^{C_t}) \geq \it{c_p} ϵmin​{−cos(FL​(x+ϵ),FLCt​​)+λ⋅∥FL​(x+ϵ)−FLCt​​∥2​},s.t.cos(FL​(x+ϵ),FLCt​​)≥cp​
Adaptive Iteration
  因为在等式中的约束条件只与损失函数的第一项有关，FIA应用以下自适应迭代来求解等式 : 第一步：我们通过设置 $\lambda =0$，开始只计算第一项损失项，直到满足约束。第二步：我们通过将 $\lambda$ 设置为一个非零值（在我们的评估中为1)，同时最小化两个损失项，以驱动 $x+ϵ$ 到目标类别 $C_t$，同时保持满足约束。当 $x+ϵ$ 分类为 $C_t$，其softmax 的最大概率大于比第二大的概率大于一个阈值，我们重复第一步，只驱动第一项损失项通过设置 $\lambda =0$ 只要 softmax 最大概率差距保持在阈值范围内。否则，就执行第二步，以此进行迭代过程。softmax距离是用来确保生成的对抗样本能够稳定的分类为目标类 $C_t$。
  如果我们把一个 $L_{\infty }$的$\delta$ 作为对抗性扰动的 $ϵ$ 边界，等式上可以用类似PGD的迭代过程来求解：
$$\begin{gathered} x_0=x, \\ {x}_{n+1}=Cli{p}_{\delta }(x_n-\eta \cdot sign({\nabla }_{x}l({\mathcal{F}}_L(x_n),{\mathcal{F}}_L^{C_t}))) \end{gathered}$$
其中 $l({\mathcal{F}}_L(x_n),{\mathcal{F}}_L^{C_t})$ 是上面的优化损失函数。

Complete Scheme

  对抗的例子生成的基本方案可能仍然无法绕过陷阱检测由于几个原因：生成层和未知的检测层之间的不匹配，不规则的不可检测边界的陷阱防御，过于简单的凸区域假设特征表示分布的目标类别。
  为了解决这些问题，我们通过两个附加功能来增强了基本方案。第一个是准备阶段，使用基本方案生成一些对抗性的示例，以查询陷阱防御，以确定适当的生成层和其他生成参数。另一个是损失函数中的一个附加项，用于将敌对的示例从在准备阶段检测到的敌对的示例停留的不良区域引导出去。

Preparation Phase： 为了确定一个合适的生成层，我们为每个潜在的生成层使用基本方案生成少量的对抗性例子，从倒数第二层开始，向后移动，以查询陷阱防御。如果检测率低于一个阈值（即，当我们考虑找到一个合适的生成层时），我们停止并选择检测率最小的层作为生成层。由于倒数第二层通常作为陷阱防御的检测层，且基本方案效果相当好（见第6.7节），因此无需搜索多个层，就可以快速找到合适的生成层。
  一旦确定了生成层，我们就使用生成层的查询结果来调整等式中的目标 ${\mathcal{F}}_L^{C_t}$ 和约束阈值 $c_p$ 将用于生成阶段。如果生成的对抗性示例都是负的，则将使用具有原始 ${\mathcal{F}}_L^{C_t}$ 和 $c_p$ 的基本方案来生成对抗性示例。如果检出率足够高（高于预设阈值），这通常发生在陷门防御对良性目标样本的高假阳性率时，我们查询陷门防御良性目标样本的检测器，直到我们收集到足够的阴性样本（我们的实验评估为10个）。在这种情况下，阴性和未测试的良性目标样本被用来计算加权平均值，对于阴性的良性样本有更多的权重（在我们的评估中是两倍）。检测到的良性目标样本（即假阳性样本）被排除在计算之外。这个加权平均值取代了基本方案中使用的 ${\mathcal{F}}_L^{C_t}$。当检测到一些生成的对抗性示例时，将调整目标 ${\mathcal{F}}_L^{C_t}$，使其远离它们如下：
$$\begin{gathered} \Delta ={\mathcal{F}}_L^{C_t}-{\mathbf{E}}_{x\in S_{pae}}{\mathcal{F}}_L(x), \\ {\mathcal{F}}_L^{C_t}\leftarrow {\mathcal{F}}_L^{C_t}+\gamma d_r\frac{\Delta }{\Vert \Delta {\Vert }_2}, \end{gathered}$$
其中 $S_{pae}$ 是正对抗样本的集合，$d_r$是生成的对抗例子的检出率， $\gamma$ 是一个正的加权参数（在我们的评估中为0.1）。
  一旦用等式确定了新的目标 ${\mathcal{F}}_L^{C_t}$，我们可以在余弦相似度上确定一个新的约束边界 $c_p$，以包含负的例子和尽可能多地排除正的例子。更具体地说，我们计算了在该阶段使用新目标 ${\mathcal{F}}_L^{C_t}$ 查询的正样本和负样本（包括良性目标样本）的余弦相似度分布。我们预设了一个百分位数范围，[𝑘𝑛𝑙，𝑘𝑛ℎ] 百分位数，以指定边界外阴性样本的阴性样本百分比的允许范围，以及一个阈值 𝑘𝑝 百分位数来指定边界外阳性样本的最小百分比。我们从负例子的分布中得到对应的第𝑘𝑛𝑙和第𝑘𝑛ℎ百分位数的𝑣𝑘𝑛𝑙和𝑣𝑘𝑛ℎ，从正例子的分布中得到对应的第𝑘𝑝百分位数的𝑣𝑘𝑝。新的约束边界 $c_p$ 的确定如下：
$$c_p=\min (v_{k_{nh}},\max (v_{k_{nl}},v_{k_p}))$$

Generation Phase
  在生成对抗性的例子时，我们将以下 drive-away 损失添加到基本方案的损失函数中在准备阶段，为了最小化与正对抗性例子的余弦相似性：
$$l_{away}({\mathcal{F}}_L(x))=\sum _{a\in S_{pae}}\cos ({\mathcal{F}}_L(x),{\mathcal{F}}_L(a))$$
将上面的损失添加到优化损失中
$$l({\mathcal{F}}_L(x),{\mathcal{F}}_L^{C_t})=-cos({\mathcal{F}}_L(x+ϵ),{\mathcal{F}}_L^{C_t})+{\lambda }_1\cdot \Vert {\mathcal{F}}_L(x+ϵ)-{\mathcal{F}}_L^{C_t}{\Vert }_2+{\lambda }_2\cdot \sum _{a\in S_{pae}}\cos ({\mathcal{F}}_L(x),{\mathcal{F}}_L(a))$$
  制作对抗示例子的迭代与基本方案相似。一开始，我们只驱使等式的第一项损失通过设置 ${\lambda }_1={\lambda }_2=0$，直到约束被满足为止。然后，我们激活 ${\lambda }_1$ 和 ${\lambda }_2$，以驱动$x$ 进入目标类别 $C_t$，并远离特征空间中的积极例子。当 $x$ 被分类为目标类别 $C_t$时，${\lambda }_1$ 将停止激活（设置为0）。当 ${\lambda }_2$ 激活时，如果等式中的第一项，其值通过乘以一个因子（在我们的评估中为1.2）来调整与最后一次迭代相比，13会减少，或者如果rst增加，则除以另一个因子。