Predicting Domain Generation Algorithms with Long Short-Term Memory Networks-优快云博客

本文链接：https://blog.youkuaiyun.com/weixin_40872714/article/details/120810989

本文解析了如何使用LSTM模型预测域名生成算法，探讨了RNN的原理，特别是LSTM在解决长序列问题的优势，以及词嵌入技术如Word2Vec在模型中的关键作用。讨论了模型结构，包括嵌入层、LSTM层和逻辑回归，并深入解析了Dropout在防止过拟合中的策略。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Predicting Domain Generation Algorithms with Long Short-Term Memory Networks 解读

RNN模型

1.为什么会有RNN模型

RNN称为循环神经网路，即一个序列当前的输出与前面的输出也有关。具体的表现形式为网络会对前面的信息进行记忆并应用于当前输出的计算中，即隐藏层之间的节点不再无连接而是有连接的，并且隐藏层的输入不仅包括输入层的输出还包括上一时刻隐藏层的输出。CNN对于简单的猫,狗,手写数字等单个物体的识别具有较好的效果. 但是, 对于一些与时间先后有关的, 比如视频的下一时刻的预测,文档前后文内容的预测等, 这些算法的表现就不尽如人意了.因此, RNN就应运而生了.

2.RNN模型

在这里插入图片描述

隐藏层的具体细节

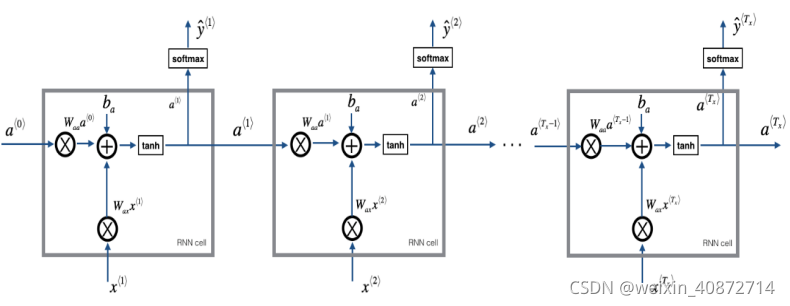
在这里插入图片描述
$a^{\langle0\rangle}$ 是激活值，通常是零向量，在 t 时刻，
$a^{\langle t \rangle} = g_1(W_{aa}a^{\langle t-1 \rangle} + W_{ax}x^{\langle t \rangle}+ b_a) \\ \hat{y}^{\langle t \rangle} = g_2(W_{ya}a^{\langle t \rangle} + by)$
上面的等式定义了神经网络的向前传播，从 $a^{\langle 0 \rangle}$ 开始，用 $a^{\langle 0 \rangle}$ 和 $x^{\langle 1 \rangle}$ 计算 $a^{\langle 1 \rangle}$ 和 $\hat{y}^{\langle 0 \rangle}$