本文详细介绍了使用Java实现二叉树的过程，包括二叉树的基本概念、存储结构、遍历算法及其实现代码。通过递归和非递归方式演示了前序、中序、后序遍历，并提供了层次遍历的实现。
上一篇博客中,使用Java实现了循环双链的LinkedList,博客链接如下:
数据结构与算法–使用Java实现循环双链的LinkedList
这篇博客,我们将使用Java.
利用链表作为底层的数据结构,来实现重要的数据结构: 二叉树.
本篇博客所涉及到的代码,均已上传到github:
项目github链接
本篇博客涉及代码github链接
本篇博客要点如下:
数据结构与算法–使用Java实现二叉树
一. 树
树状图是一种数据结构，它是由n（n>=0）个有限结点组成一个具有层次关系的集合
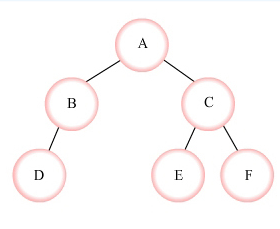
图1-1
1.1 基本概念
1.1.1 树的定义及相关概念
树的定义如下:
树（tree）是包含n（n>=0）个结点的有穷集，其中：
（1）每个元素称为结点（node）；
（2）有一个特定的结点被称为根结点或树根（root）。
（3）除根结点之外的其余数据元素被分为m（m≥0）个互不相交的集合T1，T2，……Tm-1，
其中每一个集合Ti（1<=i<=m）本身也是一棵树，被称作原树的子树（subtree）
树的一些重要的概念:
度:
结点的度: 结点拥有的子树的数目称为结点的度 例: 图1-1中结点B的度为1
树的度: 树内各节点度的最大值称为树的度 例:图1-1中树的度为2
度为0的节点称为叶子或终端节点, 例:图1-1结点D为叶子结点
度不为0的节点称为非终端节点或分支节点 例: 图1-1中结点C为分支节点
层:
结点的层次从根开始定义,层数为1个结点为根结点
树的结点的最大层数称为树的深度
关系:
父亲 : 一个结点的直接前驱结点 例: 图1-1结点A是结点B和C的父亲
儿子 : 一个结点的直接后继结点 例: 图1-1结点D是结点B的儿子
兄弟 : 同一个父亲结点的其它结点 例: 图1-1中结点B和C是兄弟
m叉树: 每个结点最多分叉的次数(m=树的度)
1.1.2 二叉树
二叉树 :
每个节点的度均不超过2的有序树,称为二叉树
每个节点的孩子数只能是0,1,2,并且孩子有左右之分
两种特殊的二叉树:
满二叉树: 如果每一层结点数都达到最大值的二叉树就是满二叉树
完全二叉树: 在一棵满二叉树中,在最下层从最右侧起去掉相邻的若干叶子节点,得到的二叉树为完全二叉树
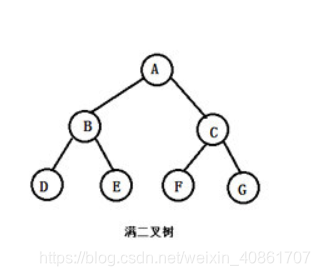
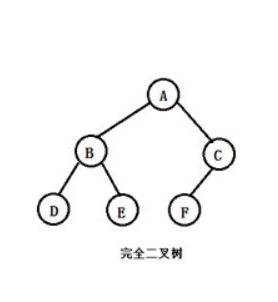
从定义和图片中我们可以看到:
满二叉树一定是完全二叉树,完全二叉树不一定是满二叉树
1.2 树的存储结构
树的存储结构分为顺序存储结构和链式存储结构
下面带大家分析下每种存储结构的特点:
1.2.1 顺序存储结构
特殊情况
满二叉树和完全二叉树:
对于这两种树来说,将其数据元素逐层存放到一组连续的存储单元中.
将二叉树中编号为i的结点存放到数组的第i个分量中
我们得到: 结点i的父结点: i / 2
结点i的左孩子: 2i, 结点i的右孩子: 2i + 1
这种存储方式对满二叉树和完全二叉树来说:
1. 存储节约空间
2. 查询性能高
图1-2
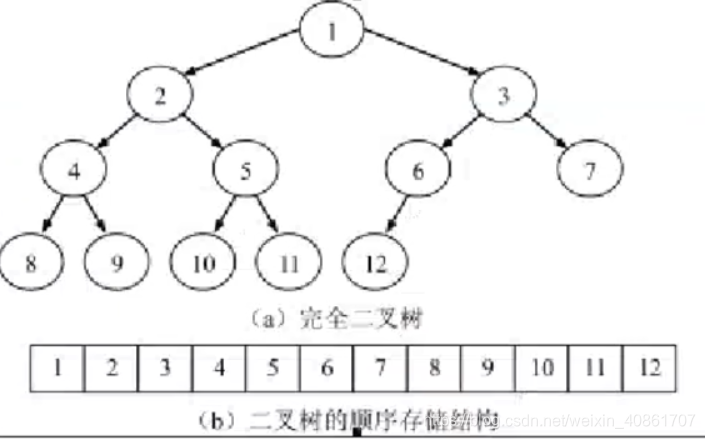但实际中,我们处理的往往是普通的树
这时,用顺序存储结构来存储树就显得笨拙了,比如下面的例子:
图1-3
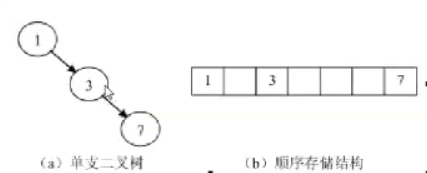
对于普通的二叉树而言,必须用"虚结点"将一棵二叉树补成一棵完全二叉树来存储
否则无法确定结点之间的前驱后继关系,但这样就会造成空间的浪费
1.2.2 链式存储结构
基于我们之前写过的双向链表, 很容易联想到
我们将二叉树每个结点设置为三个域: 包括数据域, 左孩子域和右孩子域
我们以图1-1列举的树举例
可以用下图1-4来看在链式存储结构下,树中的每个结点存储了什么内容
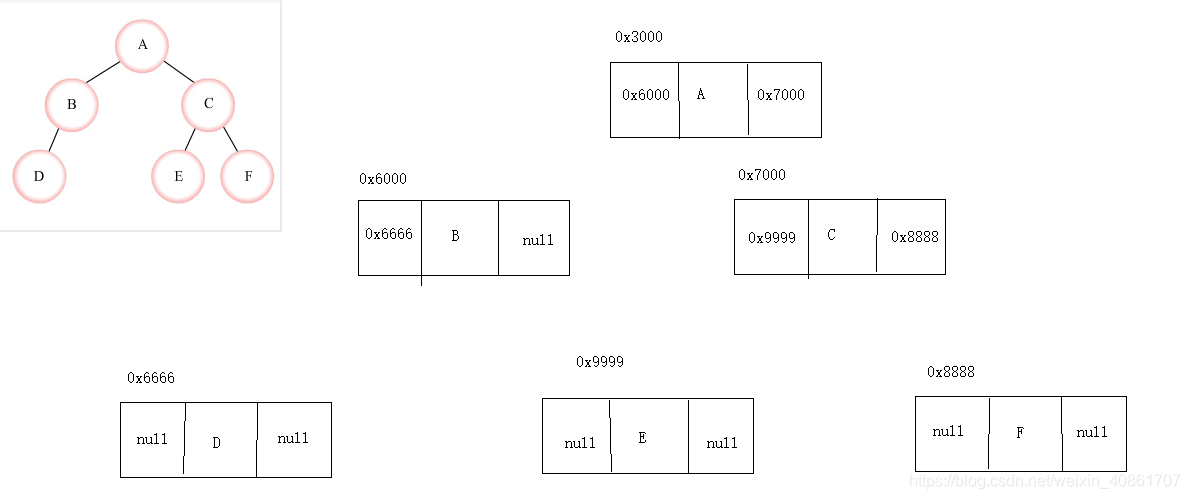通过图1-4,我们可以非常方便的通过父亲找到儿子,但是我如果想通过儿子找到父亲呢?
做不到,只能从头开始遍历
那么该如何实现这个功能? 我们这里采用了空间换时间的办法
为结点增加一个域,用来存放父亲
修改过后的存储结构如下图:
图1-5
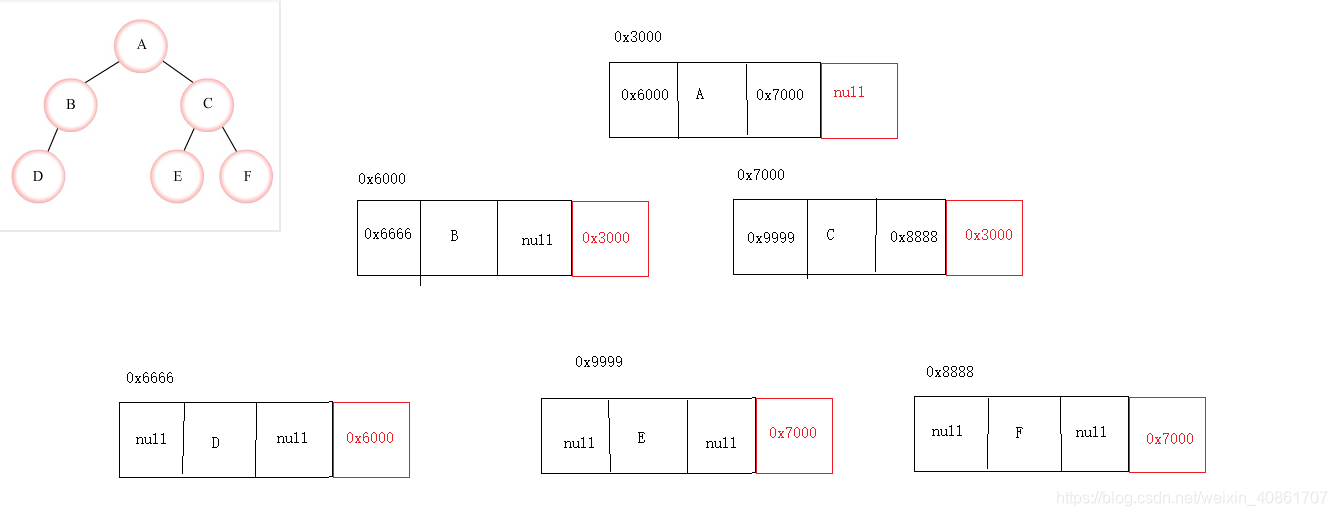
1.3 二叉树的遍历算法
遍历:
按照某种次序访问树中的所有结点,且每个结点恰好访问一次
将整个二叉树分为三部分 : 根, 左子树, 右子树
如果规定先遍历左子树,再遍历右子树.
根据根的遍历顺序我们会得到三种遍历方式
先序遍历(DLR): 根 左子树 右子树
后序遍历(LRD): 左子树 右子树 根
中序遍历:(LDR) : 左子树 根 右子树
以图1-1为例:
我们得到 :
先序遍历结果 : ABDCEF
后序遍历结果: DBEFCA
中序遍历结果: DBAECF
二.使用Java代码实现二叉树
基于上述的了解: 我们可以开始尝试使用Java实现底层是链表的二叉树
从循序渐进的角度考虑,我们使用1.2.2中提到的有三个域的列表
二叉树的常用操作如下:
获取二叉树节点数量
判断二叉树是否为空树
获取二叉树高度
查找指定结点
前序遍历
中序遍历
后序遍历
层次遍历
我们把上面列举出来的操作封装为一个方法
可以得到一个接口,如下:
2.1 BinaryTree接口
public interface BinaryTree {
boolean isEmpty(); // 判断二叉树是否为空树
int size(); // 返回二叉树的结点数量
int getHeight(); // 获取二叉树高度
Node findKey(Object value); // 查找指定结点
void preOrderTraverse(); // 前序遍历(递归)
void inOrderTraverse(); // 中序遍历(递归)
void pastOrderTraverse(); // 后序遍历(递归)
void inOrderByStack(); // 中序遍历(非递归)
void preOrderByStack(); // 前序遍历(非递归)
void postOrderByStack(); // 后序遍历(非递归)
void levelOrderByStack(); // 按照层次遍历
}
}
2.2 引入Node类
我们采用链表来描述二叉树,其中每个元素, 包含一个数据域和两个指针域(一个指向其左子树,一个指向其后子树)
我们把这种结构抽象成一个实体类Node
用Object类型的value来表示数据域
用Node类型的数据leftChild来表示该节点的左子树
用Node类型的数据rightChild来表示该节点的右子树
为了方便输出,重写一下该类的toString方法
如下面的代码所示:
/**
* @author xmr
* @date 2020/3/30 17:22
* @description 链式二叉树结点
*/
public class Node {
Object value; // 数值域
Node leftChild; // 左子树的引用
Node rightChild; // 右子树的引用
public Node(Object value, Node leftChild, Node rightChild) {
super();
this.value = value;
this.leftChild = leftChild;
this.rightChild = rightChild;
}
@Override
public String toString() {
return "[ value = " + value + " leftChild = " + leftChild + " rightChild = " + rightChild + " ]" ;
}
}
2.3 借助链表实现二叉树
我们需要定义一个成员变量来表是二叉树的根节点
因为包括遍历,查找等关键操作都是基于根节点来进行的
Node root; // 根节点
LinkedBinaryTree(Node root) {
this.root = root;
}
2.3.1 获取二叉树结点数量
对于二叉树,是没有size这个属性来直接返回结点数量给我们的
二叉树包括: 左子树,右子树,根
所以它的结点数量为 左 + 右 + 1
通过递归来实现
在二叉树的后续操作中,大量的使用递归
可以让我们更深刻的体会到递归为开发工作带来的便利
代码如下:
private int size(Node root) {
if (root == null) {
return 0;
}
int leftSize = size(root.leftChild);
int rightSize = size(root.rightChild);
return leftSize + rightSize + 1;
}
2.3.2 判断二叉树是否为空树
@Override
public boolean isEmpty() {
return root == null; // 如果根节点为空,那么二叉树为空树
}
2.3.3 获取二叉树高度
二叉树的高度为: 左子树,右子树高度的较大值 + 根节点(1)
递归操作代码实现非常简单,但往往存在输出不友好的问题
因此我们写一个方法来辅助输出,让用户层面调用方法即可
@Override
public int getHeight() {
System.out.println("二叉树的高度为: ");
int high = this.getHeight(root);
System.out.println(high);
return high;
}
private int getHeight(Node node) {
if (node == null) {
return 0;
}
// 获取左子树的高度
int leftHigh = this.getHeight(node.leftChild);
// 获取右子树的高度
int rightHigh = this.getHeight(node.rightChild);
// 返回左子树,右子树较大高度并加1
return leftHigh > rightHigh ? (leftHigh + 1) : (rightHigh + 1);
}
2.3.4 查找指定结点
private Node findKey(Object value, Node node) {
if (value == null) { // 若结点值为空
if (node == null || node.value == null) {
return node; // 结点为空或者值为空,返回
} else {
Node leftChild = this.findKey(value, node.leftChild); // 寻找结点左子树
Node rightChild = this.findKey(value, root.rightChild); // 寻找结点右子树
if (leftChild == null || leftChild.value == null) {
return leftChild; // 左结点为空或值为空则返回左结点
} else if (rightChild == null || rightChild.value == null) {
return rightChild;
} else {
return null;
}
}
}
// 当节点值非空时,非空的比较要使用equals
if (node == null) {
return null;
} else if ( value.equals(node.value)) {
return node;
} else {
Node leftChild = this.findKey(value, node.leftChild);
Node rightChild = this.findKey(value, node.rightChild);
if (leftChild != null && value.equals(leftChild.value)) {
return leftChild;
} else if (rightChild != null && value.equals(rightChild.value)) {
return rightChild;
} else {
return null;
}
}
}
接下来开始介绍二叉树的遍历
个人认为这是二叉树里最重要的内容:
2.3.5 前序遍历(递归)
遍历顺序 : 根, 左子树, 右子树
思想: 打印根的值, 然后递归遍历左子树(最终每个结点都可以看做根–>打印输出,遍历右子树)
代码实现如下:
@Override
public void preOrderTraverse() {
System.out.println("先序遍历(递归): ");
preOrderTraverse(root);
System.out.println();
}
private void preOrderTraverse(Node node) {
if (node != null) {
// 根
System.out.print(node.value + " ");
// 对左子树进行先序遍历
preOrderTraverse(node.leftChild);
// 对右子树进行先序遍历
preOrderTraverse(node.rightChild);
}
}
2.3.6 中序遍历(递归)
遍历左子树,输出根的值,遍历右子树
@Override
public void inOrderTraverse() {
System.out.println("中序遍历(递归): ");
inOrderTraverse(root);
System.out.println();
}
private void inOrderTraverse(Node node) {
if (node != null) {
// 遍历左子树
this.inOrderTraverse(node.leftChild);
// 输出根的值
System.out.print(node.value + " ");
// 遍历右子树
this.inOrderTraverse(node.rightChild);
}
}
2.3.7 后序遍历(递归)
@Override
public void pastOrderTraverse() {
System.out.println("后续遍历(递归): ");
pastOrderTraverse(root);
System.out.println();
}
private void pastOrderTraverse(Node node) {
if (node != null) {
// 遍历左子树
pastOrderTraverse(node.leftChild);
// 遍历右子树
pastOrderTraverse(node.rightChild);
// 输出根节点
System.out.print(node.value + " ");
}
}
2.3.8 按照层次遍历
层次遍历,这种遍历我借助了先进先出的队列
使用LinkedList来实现
我们看LinkedList源码,发现它实现了Deque接口
继续追踪:Deque接口实现了Queue类, 所以我们可以把LinkedList当做队列来使用, 实际上双端队列Deque,如果只能从一端删除和添加元素的话,还可以当做栈来使用,所以LinkedList这个类功能真的挺健全的哈哈
因为队列和栈不是本篇博文的重点,在这里不多介绍,
后续应该会写一篇关于队列和栈的博文
@Override
public void levelOrderByStack() {
System.out.println("按照层次遍历二叉树: ");
if (root == null) { // 空树直接返回
return;
}
Queue<Node> queue = new LinkedList<>(); // 创建队列
queue.add(root); // 把根节点添加进队列
while (queue.size() != 0) {
int length = queue.size();
for (int i= 0; i < length; i++) { // 将一层的值全部添加进来
Node temp = queue.poll(); // 出队
System.out.print(temp.value + " "); // 输出出队元素的值
if (temp.leftChild != null) {
queue.add(temp.leftChild);
}
if (temp.rightChild != null) {
queue.add(temp.rightChild);
}
}
}
System.out.println();
}
2.3.9 中序遍历(非递归)
最后,在介绍一下使用栈来进行遍历二叉树
这里以中序遍历为例
@Override
public void inOrderByStack() {
System.out.println("中序遍历(非递归): ");
Deque<Node> stack = new LinkedList<>(); // 创建栈
Node current = root;
while (current != null|| !stack.isEmpty()) {
while (current != null) {
stack.push(current); // 结点入栈
current = current.leftChild;
}
if (!stack.isEmpty()) {
current = stack.pop(); // 栈顶元素出栈
System.out.print(current.value + " ");
current = current.rightChild;
}
}
System.out.println();
}
2.4 二叉树的功能测试
接下来,我们来验证上面写的代码是否实现了我们的需求
我们依旧以图1-1所示的二叉树为例:
// 首先按照图中的结构创建好二叉树
// 创建二叉树的六个结点
Node nodeD = new Node("D", null, null);
Node nodeB = new Node("B", nodeD, null);
Node nodeE = new Node("E", null, null);
Node nodeF = new Node("F", null, null);
Node noedC = new Node("C", nodeE, nodeF);
Node nodeA = new Node("A", nodeB, noedC);
// 通过根节点,创建好树的结构
LinkedBinaryTree linkedBinaryTree = new LinkedBinaryTree(nodeA);
// 接下来对上述列出的功能进行测试
System.out.println("树是否是空树: " + linkedBinaryTree.isEmpty()); // 树是否为空
linkedBinaryTree.preOrderTraverse(); // 前序遍历(递归)
linkedBinaryTree.inOrderTraverse(); // 中序遍历(递归)
linkedBinaryTree.inOrderByStack(); // 中序遍历(非递归)
linkedBinaryTree.pastOrderTraverse(); // 后续遍历(递归)
System.out .println(linkedBinaryTree.findKey("F")); // 查找值"F"对应的节点
linkedBinaryTree.size(); // 二叉树节点个数
linkedBinaryTree.getHeight(); // 二叉树高度
linkedBinaryTree.levelOrderByStack(); // 层次遍历
程序运行的结果如下图:
可以看到,程序的结果是符合预期的,二叉树的基本功能已经实现
注: 测试可能未能覆盖全部场景,如果发现代码不严谨的地方,欢迎各位批评指正!
扫一扫
126
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
