归并排序是建立在归并操作上的一种有效的排序算法归并排序将待排序的元素序列分成两个长度相等的子序列,为每一个子序列排序,然后再将它们合并成一个序列。合并两个子序列的过程称为二路归并。
二路归并排序的算法描述:
DataList mergeSort(DataList &L){
if(Length(L)<=1) return L;
L1=mergeSort(L表中的左半侧子序列);
L2=mergeSort(L表中的右半侧子序列);
return merge(L1,L2);
};
实例分析
初始序列49,38,65,97,76,13,27
(1)将原始序列看成7个只有1个元素的子序列,显然这些子序列各自有序
(2)一趟归并:{38,49},{65,97},{13,76},{27}
(2)二趟归并:{38,49,65,97},{13,27,76}
(3)三趟归并:{13,27,38,49,65,76,97}
下面代码中merge的功能是将前后相邻的两个有序表归并为一个有序表。(
设两段有序表A[low...mid]、A[mid+1.......high]存放在同一顺序表中的相邻位置,先将它们复制到辅助数组B中。每次从对应B 中的两个段去除一个记录进行关键字的比较,将较小者放入A,当数组B中有一段下标超出其对应的表长,将另一段中的剩余部分直接复制到A中)
性能分析:时间效率:每趟归并的时间复杂度为O(n),共需进行趟归并,所以算法时间复杂度为
空间效率:merge操作辅助空间占用n个单元,所以归并排序的空间复杂度为O(n)
稳定性:不改变相同关键字的相对次序,所以稳定
#include<stdio.h>
#include<stdlib.h>
void merge(int arr[],int low,int mid,int high){
int i,j,k;
int *arrf=(int *)malloc((1000)*sizeof(int));//辅助数组
for(k=low;k<=high;k++)
arrf[k]=arr[k]; //将arr中所有元素复制到arrf中
for(i=low,j=mid+1,k=i;i<=mid&&j<=high;k++){
if(arrf[i]<arrf[j]) //比较arrf的左右两段中的元素
arr[k]=arrf[i++]; //将较小值复制到A中
else
arr[k]=arrf[j++];
}
while(i<=mid) arr[k++]=arrf[i++]; //若第一个表未检测完,复制
while(j<=high) arr[k++]=arrf[j++]; //若第二个表未检测完,复制
}
void mergeSort(int arr[],int low,int high){
if(low<high){
int mid=(low+high)/2;
mergeSort(arr,low,mid);
mergeSort(arr,mid+1,high);
merge(arr,low,mid,high);
}
}
void put(int arr[],int n){
int j;
for(j=0;j<n;j++)
printf("%d\t",arr[j]);
printf("\n");
}
void main(){
int array[]={2,1,4,3,6,5,8,7,10,9};
int i;
int len=sizeof(array)/sizeof(array[0]);
printf(" \n排序前\n");
put(array,len);
mergeSort(array,0,len-1);
printf(" \n排序后\n");
put(array,len);
}二、基数排序
它采用多关键字排序思想(基于关键字各位的大小进行排序),借助“分配”和“收集”两种操作对象对单逻辑关键字进行排序。
基数排序又分为最高位优先和最低为优先。
(比如生活中的扑克牌,假设♥>♠>♦>♣, 面值为2<3<4<5<6<7<8<9<10<J<Q<K<A
排序后(升序)则有♣2........♣A, ♦2..........♦A, ♠2........♠A, ♥2........♥A )
再来看个排序实例,初始序列为{329,457,657,839,436,720,355}
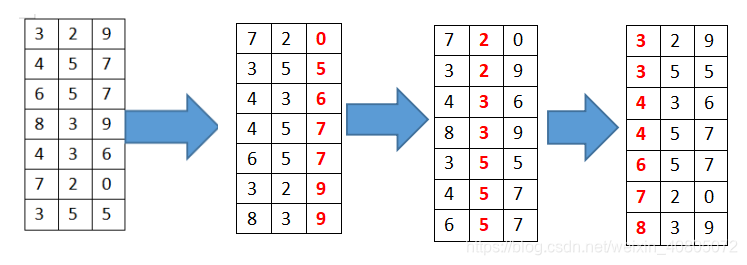
以r为为技术的最低位优先排序:假设线性表由节点序列a0到an-1构成,结点aj的关键字由d元组组成,在排序过程中使用r个队列。
对i=0,1.......d-1,依次做一次分配和收集
分配:开始时把Q0,Q1...Qr-1各个队列置为空队列,然后依次考察线性表中的每个结点aj,若aj的关键字=k ,就把aj放进Qk队列中。
收集:把Q0,Q1...Qr-1各个队列的结点依次首位相接,得到新的结点序列,从而组成新的线性表。
基数排序性能:一趟排序所需要辅助空间r个队列,以后会 重复使用这些队列,空间复杂度O(r)
时间效率:要进行d趟分配和收集,一趟分配要O(n),一趟收集要O(r),时间复杂度为O(n+r)
稳定性:稳定
这个排序如此稳定,时空复杂度如此优秀,太强了。但是,实现这个排序比较麻烦。
package mypro;
public class RadixSort
{
public static void sort(int[] number, int d) //d表示最大的数有多少位
{
int k = 0;
int n = 1;
int m = 1; //控制键值排序依据在哪一位
int[][]temp = new int[10][number.length]; //数组的第一维表示可能的余数0-9
int[]order = new int[10]; //数组orderp[i]用来表示该位是i的数的个数
while(m <= d)
{
for(int i = 0; i < number.length; i++)
{
int lsd = ((number[i] / n) % 10);
temp[lsd][order[lsd]] = number[i];
order[lsd]++;
}
for(int i = 0; i < 10; i++)
{
if(order[i] != 0)
for(int j = 0; j < order[i]; j++)
{
number[k] = temp[i][j];
k++;
}
order[i] = 0;
}
n *= 10;
k = 0;
m++;
}
}
public static void main(String[] args)
{
int[]data =
{73, 22, 93, 43, 55, 14, 28, 65, 39, 81, 33, 100};
RadixSort.sort(data, 3);
for(int i = 0; i < data.length; i++)
{
System.out.print(data[i] + " ");
}
}
}
























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








