540. Single Element in a Sorted Array-优快云博客

本文链接：https://blog.youkuaiyun.com/weixin_40801853/article/details/82355141

本文介绍了一种使用二分查找算法，在O(logn)时间复杂度内找到数组中唯一不重复元素的方法。通过两种不同的实现思路，解决了奇偶索引的问题，确保正确定位目标元素。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

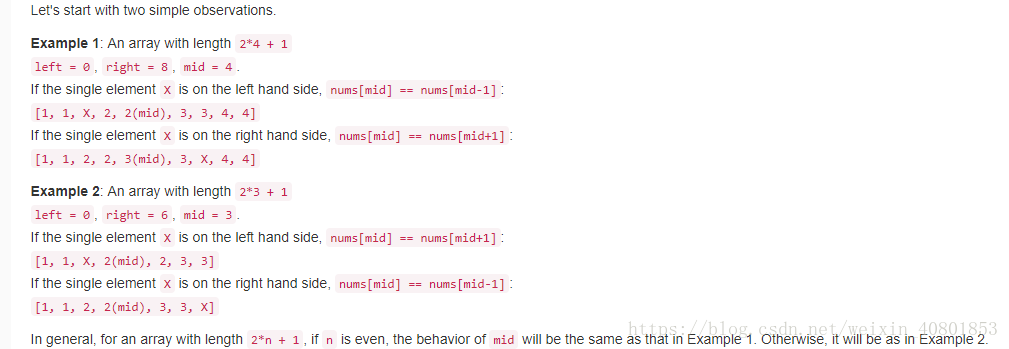
要求时间复杂度为O（logn）我最开始的思路是二分查找，对比mid处的数与mid+1、mid-1是否相同，考虑到要根据区间的奇偶需要分情况讨论，我就没有往下写，但是看到了和我思路一样的，而且他把细节都细化清楚了，如下

class Solution {
    public int singleNonDuplicate(int[] nums) {
        if(nums.length == 1) return nums[0];
        
        int len = nums.length;
        int left = 0;
        int right = len - 1;
        
        while(left <= right && left < len && right >= 0){
            int mid = left + (right - left)/2;
            
            if((mid-1 >= 0 && nums[mid-1] == nums[mid]) || (mid + 1 < len && nums[mid+1] == nums[mid])){ // nums[mid] is not single
                int currLen = right - left; // actual length - 1                
                if((currLen/2) % 2 == 0){
                    if(nums[mid-1] == nums[mid]){
                        // The element is on the left hand side
                        right = mid - 2; // Skip mid-1 and mid as we know they are not single
                    }
                    else{
                        // The element is on the right hand side
                        left = mid + 2;
                    }
                }
                else{
                    if(nums[mid-1] == nums[mid]){
                        // The element is on the right hand side
                        left = mid + 1; // Skip mid
                    }
                    else{
                        // The element is on the left hand side
                        right = mid - 1;
                    }
                }
            }
            else return nums[mid];
        }
        
        return nums[left];
    }
}

惭愧惭愧，自己懒得继续往下思考，也懒得写（其实是怕就算自己往下想了，也写不出来AC的代码==）

discussion里面有另外一种思路，是看索引的奇偶性，根据mid与mid+1,mid-1是否相等来判断这个特殊的元素是在左边区间还是右边，如下：

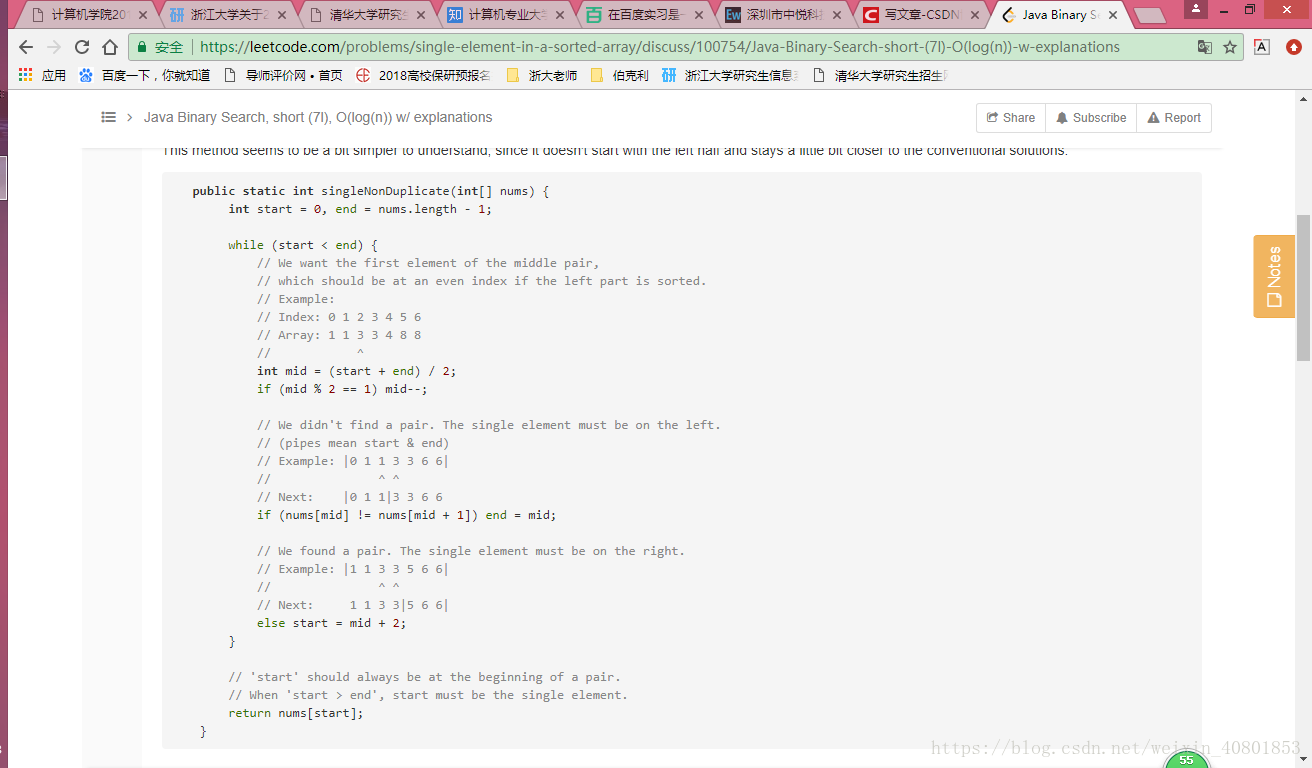
class Solution {
public int singleNonDuplicate(int[] nums) {
int start = 0 ;
int end = nums.length - 1;
while( start < end ){
int mid = ( start + end ) / 2 ;
if( mid % 2 == 1 )mid -= 1;

if( nums[ mid ] != nums[ mid + 1 ] )end = mid;
else start = mid + 2;
}
return nums[ start ];
}
}