leetcode-最大正方形之暴力和动态规划

4月30号以后就好颓废，因为确定5月11要回学校了，突然失去了在家学习的动力;
既然看不进去书，不如就写下leetcode保持手感

题目

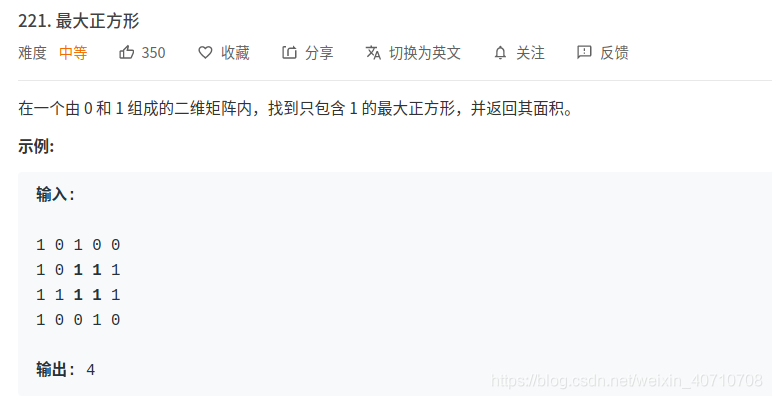首先想的没那么复杂，企图遍历整个矩阵，每个位置可能的矩阵情况被该位置的横纵坐标和矩阵的大小给限制了，因此希望以此判断每个位置的可能矩阵size是否有0; 最后有3个for循环嵌套，妥妥的超时;

暴力法代码：

class Solution {
public:
    int maximalSquare(vector<vector<char>>& matrix) {
        int j_max = matrix.size();
        if(j_max==0)
        return 0;
        int i_max = matrix[0].size();
        int area_max = 0;
        for(int i=0;i<i_max;i++)
        {
            int i_limit = i_max - i-1;
            for(int j=0;j<j_max;j++)
            {
                int j_limit = j_max - j-1;
                int size_max = min(i_limit,j_limit);
                cout<<size_max;
                for(int x=0;x<=size_max;x++)
                {
                    if(is_Square(i,j,x,matrix))
                    {
                        area_max = max(area_max,(x+1)*(x+1)); 
                        cout<<"yes";
                    }
                    else
                    break;      
                }
            }
        }
        return area_max;
    }

    bool is_Square(int n, int m, int size, vector<vector<char>> matrix)
    {
        for(int i=m;i<=m+size;i++)
        {
            for(int j=n;j<=n+size;j++)
            {
                if(matrix[i][j] == '0')
                return false;
            }
        }
        return true;
    }
};

动态规划

我们定义和矩阵matrix相同大小的dp[i][j],代表在i，j位置上构成矩阵的最长边长，若某一位置为‘1’，那么该位置的dp值取决于它左，上，左上三个方向上dp的值，状态转移方程：
dp[i][j] = min(dp[i-1][j],min(dp[i][j-1],dp[i-1][j-1]))+1;

class Solution {
public:
    int maximalSquare(vector<vector<char>>& matrix) {
        int j_max = matrix.size();
        if(j_max==0)
        return 0;
        int i_max = matrix[0].size();
        int dp[i_max][j_max];
        for(int i=0;i<i_max;i++)
        {
            for(int j=0;j<j_max;j++)
            dp[i][j]=0;
        }
        //初始化dp矩阵全为0
        int side_max = 0;
        //side_max是保存目前已发现的最长边
        for(int i=0;i<i_max;i++)
        {
            for(int j=0;j<j_max;j++)
            {
                if(matrix[j][i] == '1')
                {
                    if(i==0 || j==0)
                    dp[i][j] = 1;
                    //i=0或j=0是特殊情况
                    else
                    dp[i][j] = min(dp[i-1][j],min(dp[i][j-1],dp[i-1][j-1]))+1;
                    side_max = max(side_max,dp[i][j]);
                }
 
            }
        }
        return side_max*side_max;
    }
};