力扣28：实现 strStr()

原题链接
这题对于初学者有多恶心呢？给你们看看我的败绩…

KMP算法讲解

我先是看了官方解答，前面的还好懂，到了后面讲优化部分就彻底歇菜了，讲的太抽象太跳跃。
然后我看了宫水三叶前辈的解法。

假设原串为 abeababeabf，匹配串为 abeabf。首次匹配的「发起点」是第一个字符 a。显然，后面的 abeab 都是匹配的，两个指针会同时往右移动（黑标）。
在都能匹配上 abeab 的部分，「朴素匹配」（暴力解）和「KMP」并无不同。直到出现第一个不同的位置（红标）：

接下来，正是「朴素匹配」和「KMP」出现不同的地方：
先看下「朴素匹配」逻辑：

1. 将原串的指针移动至原串的本次「发起点」的下一个位置（b 字符处）；匹配串的指针移动至匹配串的起始位置。
2. 尝试匹配，发现对不上，原串的指针会一直往后移动，直到能够与匹配串对上位置。
   如图：
   
   也就是说，对于「朴素匹配」而言，一旦匹配失败，将会将原串指针调整至下一个「发起点」，匹配串的指针调整至起始位置，然后重新尝试匹配。
   这也就不难理解为什么「朴素匹配」的复杂度是 O(m∗n) 了。

然后我们再看看「KMP 匹配」过程。首先匹配串会检查之前已经匹配成功的部分中里是否存在相同的「前缀」和「后缀」。如果存在，则跳转到「前缀」的下一个位置继续往下匹配。这里的跳转，相当于原串的发起点跳到了该后缀的开头(第4个字符a)，原串的指针的位置保持不变(也就是第6个字符a），匹配串的指针跳回到前缀的下一个位置（也就是第3个字符e）：

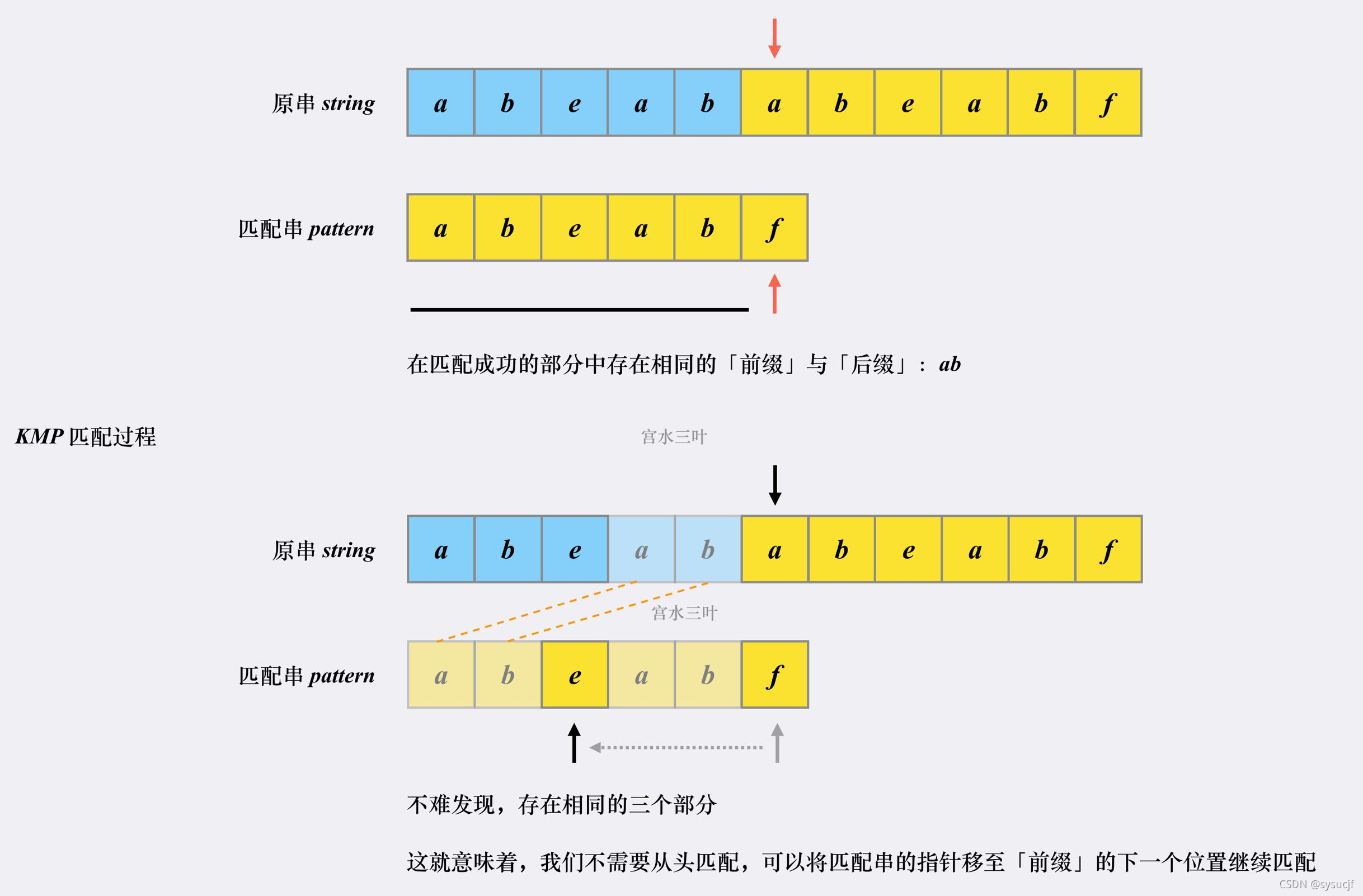
跳转到下一匹配位置后，尝试匹配，发现两个指针的字符对不上（也就是原串第6个字符a和匹配串第3个字符e），并且此时匹配串指针前面不存在相同的「前缀」和「后缀」(匹配串的指针前面为ab)，这时候只能回到匹配串的起始位置重新开始（原串指针位置不变，相当于原串发起点跳到原串指针所在处。匹配串指针跳回到匹配串起点）：

实际上可以发现，原串的指针要么是在匹配串指针调整的时候不动，要么是跟着匹配串指针一直向后读取；匹配串指针要么总是跳到已匹配部分的“前缀”的下一位，要么回到起点

到这里，你应该清楚 KMP 为什么相比于朴素解法更快：

• 因为 KMP 利用已匹配部分中相同的「前缀」和「后缀」来加速下一次的匹配。-
• 因为 KMP 的原串指针不会进行回溯（没有朴素匹配中回到下一个「发起点」的过程）。

其实是意味着：随着匹配过程的进行，原串指针的不断右移，我们本质上是在不断地在否决一些「不可能」的方案。

当我们的原串指针从 i 位置后移到 j 位置，不仅仅代表着「原串」下标范围为 [i,j) 的字符与「匹配串」匹配或者不匹配，更是在否决那些以「原串」下标范围为 [i,j) 为「匹配发起点」的子集。

优化

我们可以先分析一下复杂度。如果严格按照上述解法的话，最坏情况下我们需要扫描整个原串，复杂度为 O(n)O(n)。同时在每一次匹配失败时，去检查已匹配部分的相同「前缀」和「后缀」，跳转到相应的位置，如果不匹配则再检查前面部分是否有相同「前缀」和「后缀」，再跳转到相应的位置 … 这部分的复杂度是O(m²)（还记得首项+末项的和乘以项数除以2），因此整体的复杂度是O(n*m²)。而我们的朴素解法是O(m∗n) 的。
说明还有一些性质我们没有利用到。
显然，扫描完整原串操作这一操作是不可避免的，我们可以优化的只能是「检查已匹配部分的相同前缀和后缀」这一过程。
再进一步，我们检查「前缀」和「后缀」的目的其实是「为了确定匹配串中的下一段开始匹配的位置」。
同时我们发现，对于匹配串的任意一个位置而言，由该位置发起的下一个匹配点位置其实与原串无关。
举个 例子，对于匹配串 abcabd 的字符 d 而言，由它发起的下一个匹配点跳转必然是字符 c 的位置。因为字符 d 位置的相同「前缀」和「后缀」字符 ab 的下一位置就是字符 c。
可见从匹配串某个位置跳转下一个匹配位置这一过程是与原串无关的，我们将这一过程称为找 next 点。
显然我们可以预处理出 next 数组，数组中每个位置的值就是该下标应该跳转的目标位置（ next 点）。
当我们进行了这一步优化之后，复杂度是多少呢？
预处理 next 数组的复杂度未知，匹配过程最多扫描完整个原串，复杂度为 O(n)。
因此如果我们希望整个 KMP 过程是 O(m + n) 的话，那么我们需要在 O(m)的复杂度内预处理出 next数组。
所以我们的重点在于如何在 O(m) 复杂度内处理处 next 数组。

设有匹配串 aaabbab，我们来看看对应的 next 是如何被构建出来的。

1. i=1,j=0
   p[0]=p[1]=a;next[1]=0+1=1;i,j各后移一位。
2. i=2,j=1
   p[1]=p[2]=a;next[2]=+1+=2;i,j各后移一位

i=3,j=2。这时p[3]=b,p[2]=a。那么j就应该跳转到j=next[j-1]=next[2-1]=next[1]=1的位置(为什么这么跳转呢？可以看官方解答的给出一个i如何定位j的解释，给出了很严谨的数学证明。
i=3,j=1。这时p[3]=b,p[1]=a。还是不相等，因此j继续跳转。j=next[j-1]=next[0]=0。此时也已经抵达了循环的边界条件：p[j]=p[i]或者j=0。
i=3,j=0。这时p[3]=b,p[0]=a。还是不相等，j不能跳转了。这个时候就只能取next[i]=0了（没有前缀所以前缀长度为0）。如果循环终止时p[i]!=p[j]，i向后移动一位而j不动（并非i,j同时后移一位）。（循环终止时如果p[i]=p[j]，则next[i]=j+1，然后i,j向后移一位）

i=4,j=0。这时p[4]=b,p[0]=a。两者不相等，j=0所以j不能跳转了。这个时候就只能取next[4]=next[i]=0了。如果循环终止时p[i]!=p[j]，i向后移动一位而j不动。
i=5,j=0。这时p[5]=a,p[0]=a。next[5]=0+1=1;i,j各后移一位。

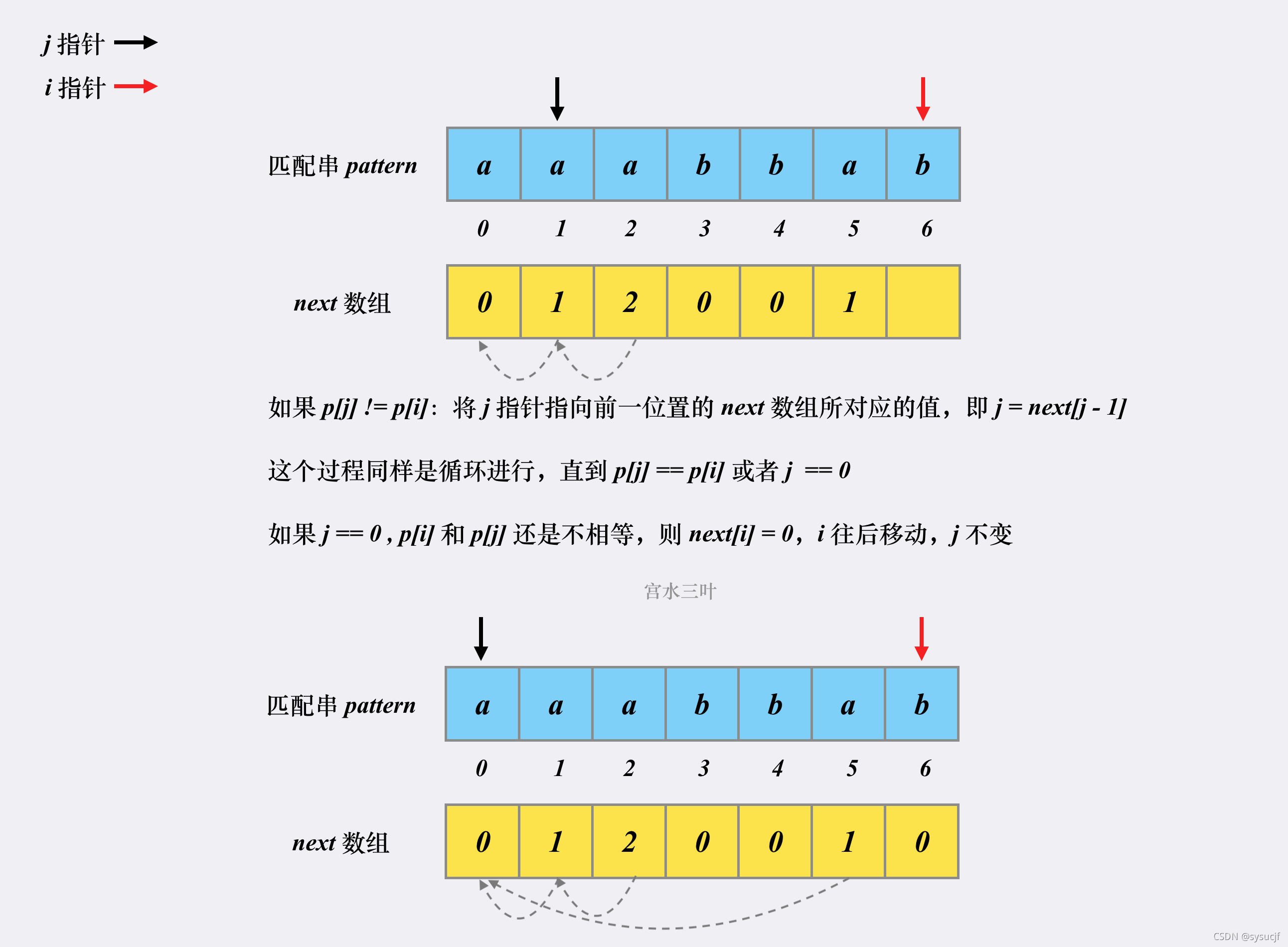
i=6,j=1。这时p[6]=b,p[1]=a。两者不相等。那么j就应该跳转到j=next[j-1]=next[1-1]=next[0]=1的位置。跳出循环
i=6,j=0。这是p[6]=b,p[0]=a。两者还是不相等，因此next[6]=0。i后移一位，j不动。
这就是整个 next 数组的构建过程，时空复杂度均为 O(m)。整个 KMP 匹配过程复杂度是 O(m+n) 的。

代码实现

在实际编码时，通常我会往原串和匹配串头部追加一个空格（哨兵）。目的是让 j 下标从 0 开始，省去 j 从 -1 开始的麻烦。
整个过程与上述分析完全一致，一些相关的注释我已经写到代码里。

class Solution {
    // KMP 算法
    // ss: 原串(string)  pp: 匹配串(pattern)
    public int strStr(String ss, String pp) {
        if (pp.isEmpty()) return 0;
        
        // 分别读取原串和匹配串的长度
        int n = ss.length(), m = pp.length();
        // 原串和匹配串前面都加空格，使其下标从 1 开始
        ss = " " + ss;
        pp = " " + pp;

        char[] s = ss.toCharArray();
        char[] p = pp.toCharArray();

        // 构建 next 数组，数组长度为匹配串的长度（next 数组是和匹配串相关的）
        int[] next = new int[m + 1];
        // 构造过程 i = 2，j = 0 开始，i 小于等于匹配串长度 【构造 i 从 2 开始】
        // i从2开始也就是从p的第3个字符，匹配串的第2个字符开始，符合前面的分析
        // j从0开始，这样j+1就可以从1开始，也就是匹配串的第1个字符开始，符合前面的分析
        // i指向当前迭代的子串终点字符
        // j指向当前迭代的上一个迭代的子串的前缀的终点字符
        for (int i = 2, j = 0; i <= m; i++) {
            // 匹配不成功的话，j = next(j)
            while (j > 0 && p[i] != p[j + 1]) j = next[j];
            // 匹配成功的话，先让 j++
            if (p[i] == p[j + 1]) j++;
            // 更新 next[i]，结束本次循环，i++
            next[i] = j;
        }

        // 匹配过程，i = 1，j = 0 开始，i 小于等于原串长度 【匹配 i 从 1 开始】
        // i指向当前迭代的原串的字符
        // j用来定位匹配串与子串比较时应该从哪里比较，p[1:j]=s[i-j+1:i]
        for (int i = 1, j = 0; i <= n; i++) {
            // 匹配不成功 j = next(j)
            while (j > 0 && s[i] != p[j + 1]) j = next[j];
            // 匹配成功的话，先让 j++，结束本次循环后 i++
            if (s[i] == p[j + 1]) j++;
            // 整一段匹配成功，直接返回下标
            if (j == m) return i - m;
        }

        return -1;
    }
}

• 时间复杂度：n 为原串的长度，m 为匹配串的长度。复杂度为 O(m+n)。
• 空间复杂度：构建了 next 数组。复杂度为 O(m)。

补充

将字符串使用toCharArray转化为字符数组来遍历比直接使用charAt遍历更快