二阶矩阵转置怎么求_Fortran矩阵转置和乘法运算

Fortran在科学计算方面有强大运算能力，主要是体现在矩阵上，Fortran专门为矩阵的应用设计了很多专用函数。

对于一个矩阵的转置矩阵，简单来讲，就是行变列。如果用标准程序来写，就是两个循环，然后行列交换。有矩阵A，它的转置矩阵为矩阵B。

  do i=1,im        do j=1,jm            b(j,i)=a(i,j)        end do    end do

Fortran专门有矩阵转置的函数。b=transpose(a)。这和上面的代码是等效的。

两个矩阵相乘，要求只有在第一个矩阵的列数(column)和第二个矩阵的行数(row)相同时才有意义。

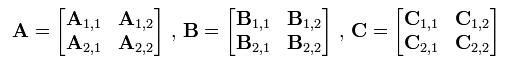
矩阵A*矩阵B=矩阵C

矩阵相乘结果满足如下公式：

1. C11=A11B11+A12B21
2. C12=A11B12+A12B22
3. C21=A21B11+A22B21
4. C22=A21B12+A22B22

用标准代码就是：

  do i=1,im        do j=1,im            c(i,j)=0            do k=1,jm                c(i,j)=c(i,j)+a(i,k)*b(k,j)            end do        end do    end do

Fortran专门有矩阵相乘的函数。c=matmul(a,b)。这和上面代码是等效的。

我们做一个练习，把一个3*3矩阵A，分别通过代码和函数公式求出转置矩阵B，然后再分别通过代码和函数公式计算A,B相乘得到矩阵C。

program test70    implicit none    integer,parameter::im=3,jm=3    integer::i,j,k    integer::a(im,jm),b(jm,im),c(im,im)=0    data a &        /1,2,3,&         5,9,4,&         7,2,6/    write(*,*)"矩阵A:"    write(*,"(3i2)")a    write(*,'(60("-"))')    do i=1,im        do j=1,jm            b(j,i)=a(i,j)        end do    end do    write(*,*)"循环求矩阵B:"    write(*,"(3i2)")b    write(*,'(60("-"))')    b=transpose(a)    write(*,*)"公式求矩阵B:"    write(*,"(3i2)")b    write(*,'(60("-"))')    do i=1,im        do j=1,im            c(i,j)=0            do k=1,jm                c(i,j)=c(i,j)+a(i,k)*b(k,j)            end do        end do    end do    write(*,*)"循环求矩阵A*B:"    write(*,"(3i4)")c    write(*,'(60("-"))')     c=matmul(a,b)    write(*,*)"公式求矩阵A*B:"    write(*,"(3i4)")c    write(*,'(60("-"))')           pause    stopend program test70

运行程序，结果如下：(Fortran矩阵顺序是先列后行)

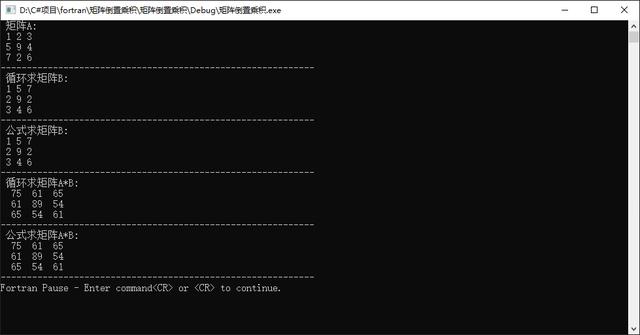
运行结果

Fortran中两个矩阵可以直接相加，相减。大大提高了运行效率。