二重积分转换成极坐标_高数8.2二重积分的计算

介绍完二重积分的定义和性质，我们下面就来看如何计算二重积分。计算二重积分有很多方法，最朴实的一种方法，就是将一个二重积分转换成一个由两个步骤组成的单重积分。细究起来又可以进一步分成直角坐标、极坐标等方法。因为计算二重积分可以由很多种方法，也不算是我们学习的重点，因此就用几个例子来带过。

例1：计算积分

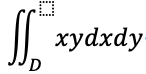
的值，其中积分区域D是由抛物线y²=x和直线y=x-2所围成的封闭区域。

我们先画出积分区域来进行观察：

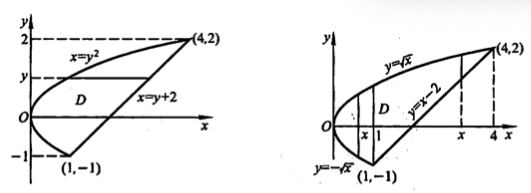
很显然，先按照y值进行切分(横切)会相对容易，因为在整个y的定义域(-1,2)上不涉及到函数值的变化，x都是从y²到y+2。

如果按照x来进行切分(竖切)则会相对复杂，因为x的值从(0,1)上，y是从-根号x到根号x，x的值从(1,4)上，y是从x-2到根号x，这样就相对于按照y值切分要麻烦很多，因此我们选择第一种方法。

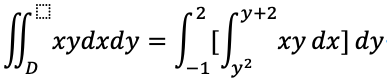
这样分层以后，对于内层的，对x的积分，y可以看成是常数，因此就可以从内向外的分解积分了：

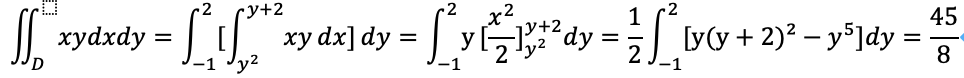
因此，对于二重积分来说，选择积分顺序是个技术活，需要很多经验和对积分域的观察，对于多重积分来说就更甚了。