Summary
层次分析法在最近的数据咨询案例中经常遇到,其实它是一个很简单有方法可循的常用多目标规划方法。在本文中你将了解到:层次分析法的用途;层次分析模型构造过程;不需要手算和编程的yaahp层次分析法软件介绍;如何构造判断矩阵以便能一次性通过一致性检验。通晓了如何构造判断矩阵以及熟练掌握yaahp层次分析法软件,相信层次分析不再是你建模、科研路上的拦路虎。
如果想获得yaahp层次分析法软件(软件与详细使用教程)以及“数学模型(姜启源)pdf电子书(层次分析法在P249,可以帮助深入了解层次分析)”,请将本文转发到朋友圈或一个群(QQ或微信),然后截图发给微信公众号后台(统计程序狗),顺便留下您的邮箱即可哦~
引言
多目标决策即具有多种选择的目标决策问题。例如,挑选男朋友就是一个多目标决策问题。不同的人对如何找一个理想的男朋友的标准是不同的,有的人更看重相貌,有的人更看重经济条件。但是,许多女孩经常面对的情况是“长得丑的男生家庭条件好“,”长得好看的男生能力又有点欠缺”。因此,在做出选择的时候,我们都会不同程度的因迁就一些因素从而换取自己比较看重的因素,那么当有几个备选男朋友出现而你又难以做出选择时,如何根据自己的喜好,使用可以量化的方法“综合”地选出一个最理想的男朋友呢?这就是多目标决策问题,而层次分析法就是解决这类问题的一个非常重要的手段。因此有诗云:层次选的妙,脱单会更早;分析做的好,爱情更加牢。
层次分析法介绍
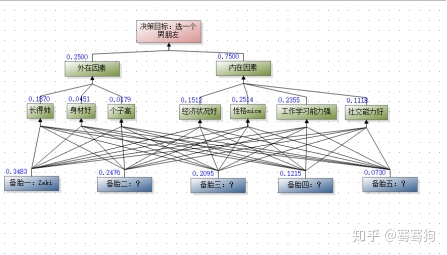
层次分析法的基本思想是把复杂问题分解为若干层次,在每一层次通过两两对比得出判断矩阵、然后计算各因素的权重,接着由低到高地层层分析计算,最后得出各方案对总目标的权重,权重最大的方案即为最优方案。如图1所示,“选一个男朋友”是目标层,目标层一般只有一个;中间的绿色框是准则层和指标层,即我们要考虑的因素;最后蓝色框是方案层,我们的目的是在准则层和指标层下,综合得出相对于目标层而言最优的一个方案。何为最优,层次分析法有一套数学计算方法,最后方案层的每一个方案都会对应一个权重,权重最大者即最优。
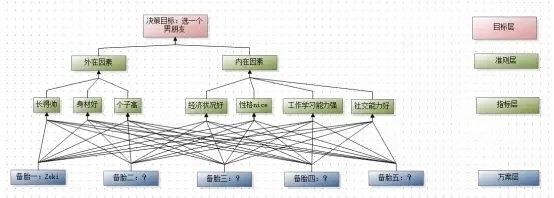
图1
判断矩阵
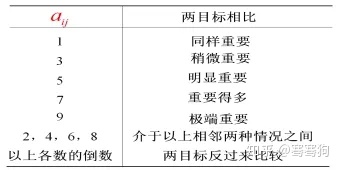
层次分析的第一步是要对准则层、指标层和方案层的因素进行两两比较从而建立判断矩阵,所谓判断矩阵即每一层的几个因素相对于上一层某一个因素的相对重要性。比如对于外在因素,你觉得“长得帅”、“身材好”以及“个子高”的相对重要性是怎样的?比如有的人认为:长得帅比身材好重要,长得帅比个子高重要,身材好比个子高重要。但是重要的程度又怎样界定呢?可以参考下表:
表1
其中,
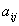
表示判断矩阵中第i行第j列的元素,也是第i行个因素比第j列个因素的相对重要性,自然的如果
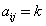
,那么
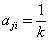
。
由表1,我们可以进一步作出这样的判断:在外在因素中,“长得帅”比“身材好”明显重要,长得帅比个子高极端重要,身材好比个子高稍微重要,那么判断矩阵就是:

判断矩阵的建立是为了得出“长得帅、身材好、个子高”对于决策所占的权重,而权重的得出是用判断矩阵的特征向量表示的。特征向量的涵义即为相对于外在因素,“长得帅”、“身材好以及“个子高”的对于作出决策的重要程度,我们计算出的结果为(0.7482, 0.1804, 0.0714),所以长得帅、身材好、个子高对于外在因素的重要性依次为0.7482,0.1804,0.0714,像这样,依次构造每一层相对于上一层某因素的判断矩阵并计算权重。然而,我们的目标是做出决策,因此还需要建立目标层“选一个男朋友”与方案层“各备胎”之间的联系。这就需要计算出合成权重,合成权重即为在考虑所有内外在因素的前提下,各备胎的权重比较结果,权重最大者即是最佳男友。
yaahp层次分析法软件
关于方案层对于目标层的合成权重以及判断矩阵的特征向量计算过程十分繁琐,这里我们给大家介绍一个非常容易操作的层次分析软件(yaahp层次分析法软件),这个软件可以帮我们免去层次分析法复杂的计算过程,直接得出最佳决策。
第一步:运行软件。

打开软件后,主要分为三个部分,分别是“层次结构模型”,“判断矩阵”以及“计算结果”三个主要界面。
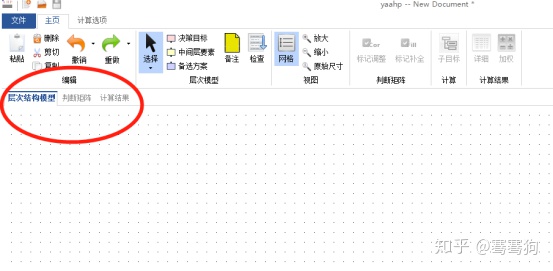
第二步:在“层次结构模型”界面中,通过工具栏进行层次结构目标层、准则层、指标层以及方案层的绘制;
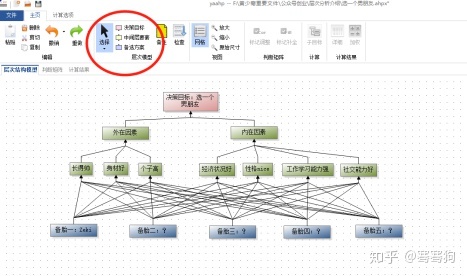
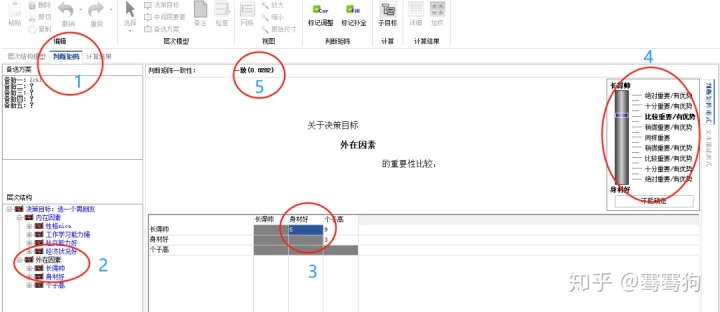
第三步:判断矩阵的输入
进入“判断矩阵”界面(椭圆1)。在椭圆2处选择对哪个因素设计判断矩阵。点击椭圆3,设计“长得好”相对于“身材好”的重要性(滑动椭圆4中的蓝色光柱)。在椭圆5中直接会出现一致性检验结果,如果一致性检验不通过还得继续调整判断矩阵。依次输入完所有的判断矩阵。
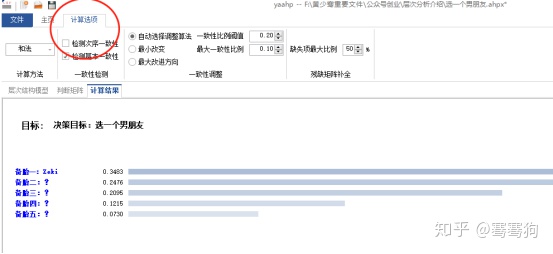
第四步:进入“计算结果”界面(椭圆1)。即可以看出各备胎的合成权重(椭圆2)。

点击上图中详细结果(椭圆3),即可见所有计算过程当中的结果(下图)。
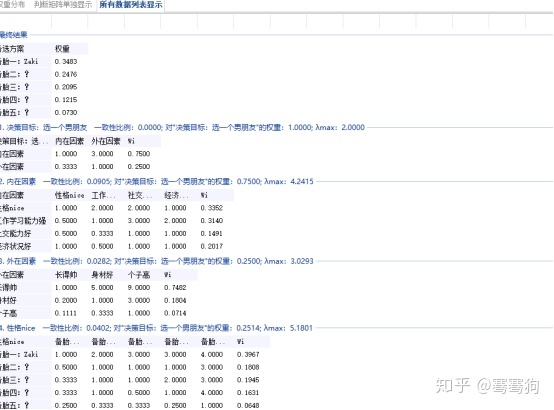
没错,最后我们就完成了层次分析,从中可以看出,综合内外在因素,从各个方面综合考虑,最优秀的还是Zeki(自恋的家伙)!!!
当然,点击如下计算选项,有更多的计算功能,还有待大家去开发哦!
关注请微信搜索:统计程序狗(微信号:statistical_dog)






















 4891
4891

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








