多元线性回归（sklearn实现）

首先我们先看数据集以及我们要解决的问题

数据集如下：

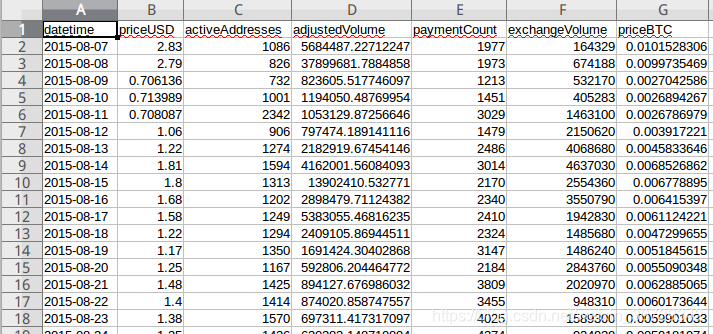
要解决的是分析priceUSB与其他因素的关系，做出关系式，也就是Y为priceUSD，X分别为其他5个因素，做出多元线性回归方程。

①分析下每个因素和Y的关系（这一步就是只是看个开心而已其实）

def display_lr():
    pd_data=pd.read_csv('eth.csv')#原始数表
    #画出单因素拟合情况
    print('pd_data.head(10)=\n{}'.format(pd_data.head(10)))
    # mpl.rcParams['font.sans-serif'] = ['SimHei']  #配置显示中文，否则乱码
    mpl.rcParams['axes.unicode_minus']=False #用来正常显示负号，如果是plt画图，则将mlp换成plt
    sns.pairplot(pd_data, x_vars=['activeAddresses','adjustedVolume','paymentCount','exchangeVolume','priceBTC'], y_vars='priceUSD',kind="reg", size=5, aspect=0.7)
    plt.show()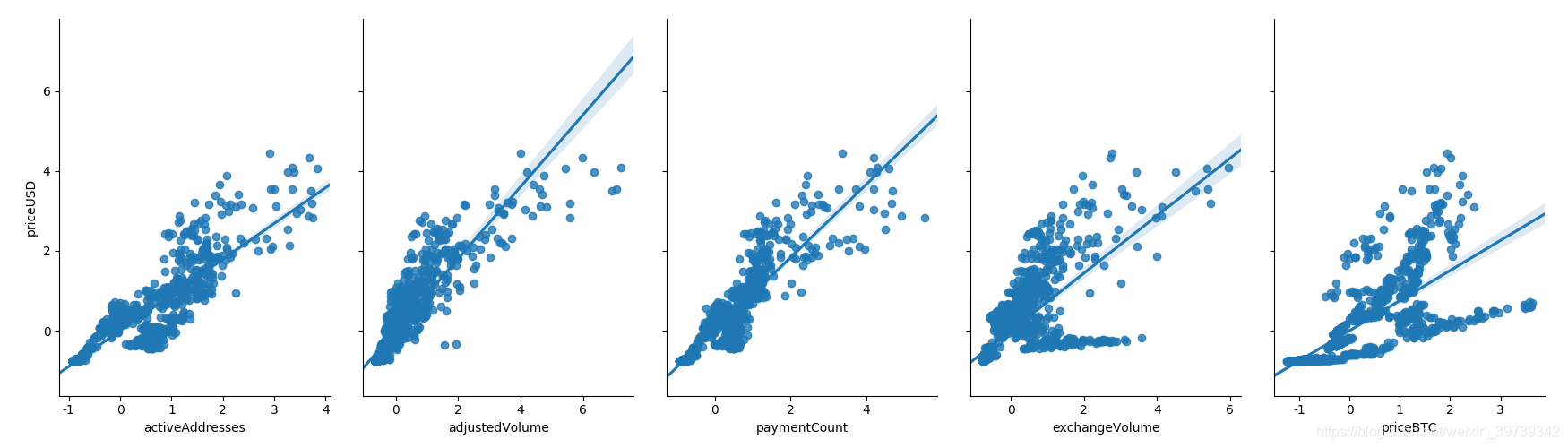

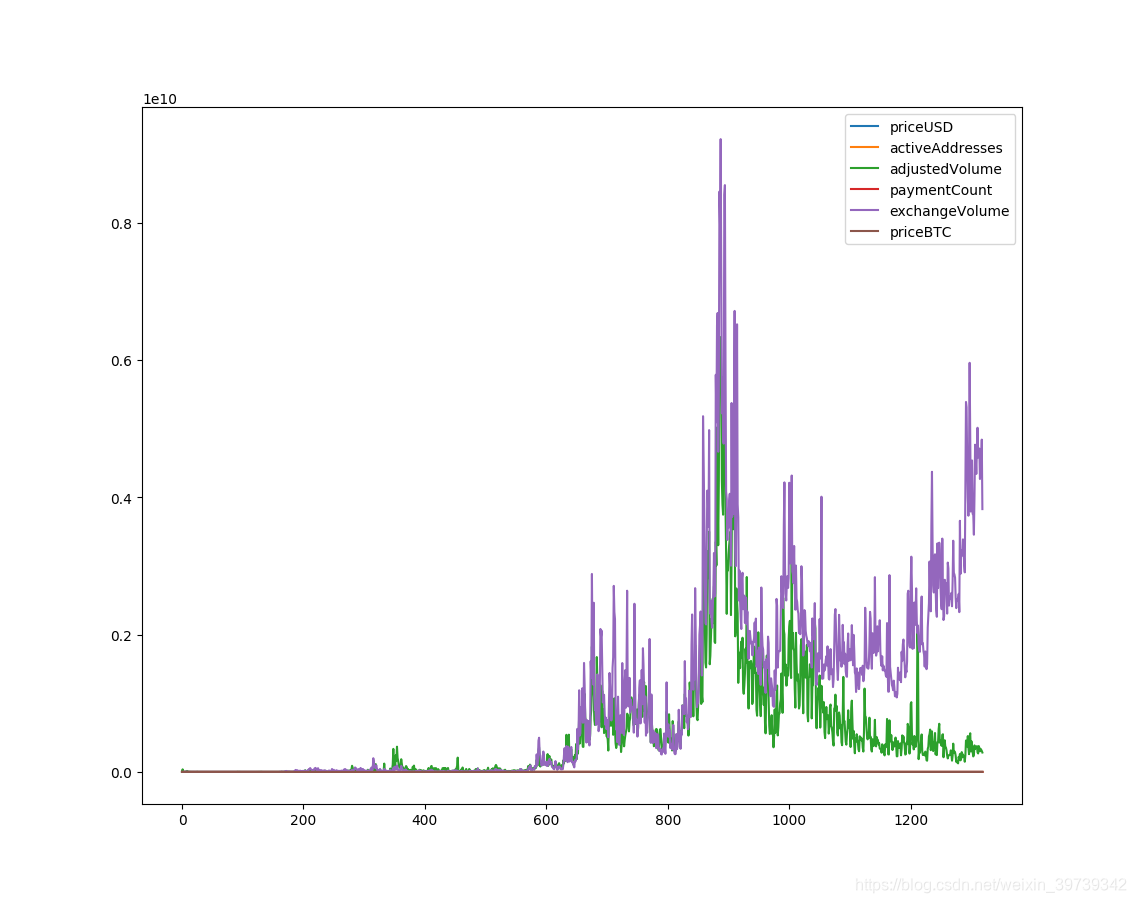
②数据归一化（数据存在差异性过大，需要归一化统一处理）

def Normalization():
    #对数据进行归一化处理 并存储到eth2.csv
    pd_data=pd.read_csv('eth.csv')
    sam=[]
    a=['priceUSD','activeAddresses','adjustedVolume','paymentCount','exchangeVolume','priceBTC']
    for i in a:
        y = pd_data.loc[:, i]
        ys = list(preprocessing.scale(y))  # 归一化
        sam.append(ys)

    print len(sam)
    with open('eth2.csv', 'w') as file:
        writer = csv.writer(file)
        for i in range(len(sam[0])):
            writer.writerow([sam[0][i],sam[1][i],sam[2][i],sam[3][i],sam[4][i],sam[5][i]])
    print('完毕')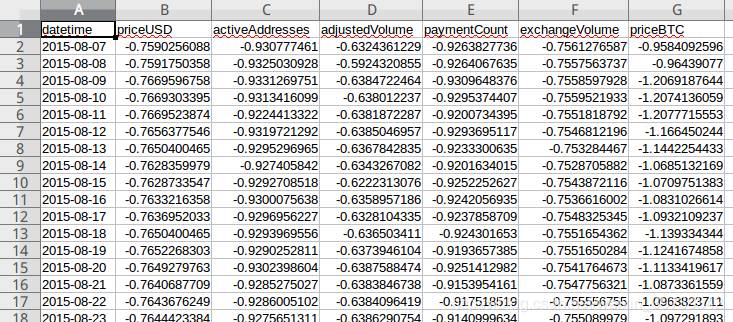

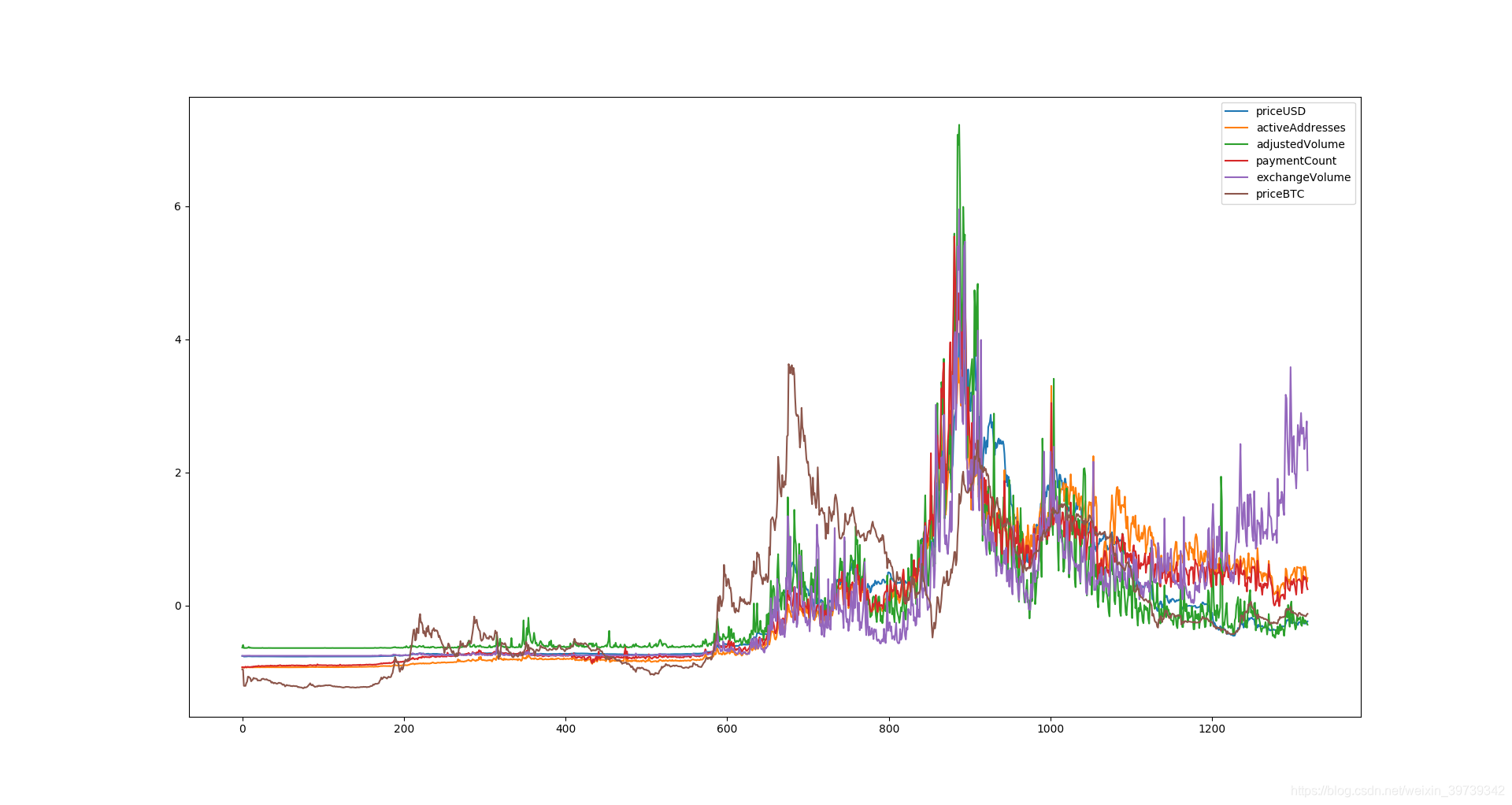
③利用sklearn的LinearRegression进行训练，训练集：测试集=8:2

from sklearn.model_selection import train_test_split #这里是引用了交叉验证
from sklearn.linear_model import LinearRegression  #线性回归

def build_lr():
    X = pd_data.loc[:, ('activeAddresses','adjustedVolume','paymentCount','exchangeVolume','priceBTC')]
    y = pd_data.loc[:, 'priceUSD']
    X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=532)#选择20%为测试集
    print('训练集测试及参数:')
    print('X_train.shape={}\n y_train.shape ={}\n X_test.shape={}\n,  y_test.shape={}'.format(X_train.shape,
                                                                                               y_train.shape,
                                                                                               X_test.shape,
                                                                                               y_test.shape))
    linreg = LinearRegression()
    #训练
    model = linreg.fit(X_train, y_train)
    print('模型参数:')
    print(model)
    # 训练后模型截距
    print('模型截距:')
    print linreg.intercept_
    # 训练后模型权重（特征个数无变化）
    print('参数权重:')
    print (linreg.coef_)

    y_pred = linreg.predict(X_test)
    sum_mean = 0
    for i in range(len(y_pred)):
        sum_mean += (y_pred[i] - y_test.values[i]) ** 2
    sum_erro = np.sqrt(sum_mean /len(y_pred))  # 测试级的数量
    # calculate RMSE
    print ("RMSE by hand:", sum_erro)
    # 做ROC曲线
    plt.figure()
    plt.plot(range(len(y_pred)), y_pred, 'b', label="predict")
    plt.plot(range(len(y_pred)), y_test, 'r', label="test")
    plt.legend(loc="upper right")  # 显示图中的标签
    plt.xlabel("the number of sales")
    plt.ylabel('value of sales')
    plt.show()

输出如下

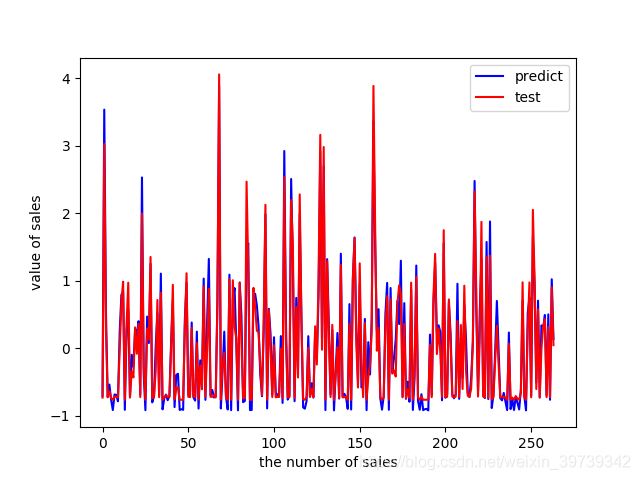
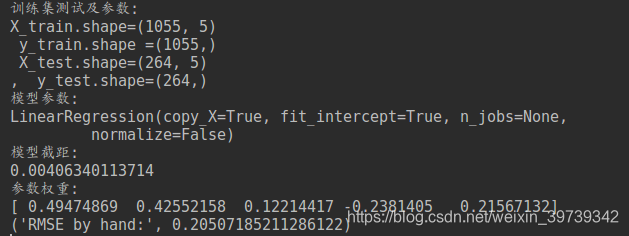
对于这份数据而言，由于priceUSD的价格不单单由上诉因素决定，以及波动性较大，所以RMSE为0.20507在此处算是一个较好的结果。

所以我们可以得出我们的结果（大致的过程就这样了）

④最后写一个测试程序看一下总体结果是怎样的

def Compared():
    #利用方程进行拟合 对比 并存储数据到eth3.csv
    pd_data = pd.read_csv('eth2.csv')
    sam=[]
    a=['priceUSD','activeAddresses','adjustedVolume','paymentCount','exchangeVolume','priceBTC']
    dic={}
    for i in a:
        y = pd_data.loc[:, i]
        dic[i] = list(y)  # 归一化
    print(dic)
    for i in range(len(dic['priceUSD'])):
        x = 0.00406340113944 + float(dic['activeAddresses'][i])*0.49474868663194016+float(dic['adjustedVolume'][i])*0.42552157541384+float(dic['paymentCount'][i])*0.12214416604623446 +float(dic['exchangeVolume'][i])*(-0.23814049518276936) +float(dic['priceBTC'][i])* 0.21567132432245326
        sam.append(x)

    with open('eth3.csv', 'w') as file:
        writer = csv.writer(file)
        writer.writerow(['priceUSD','Predictive value'])
        for i in range(len(sam)):
            writer.writerow([dic['priceUSD'][i],sam[i]])
    print('完毕')
    pd_data=pd.read_csv('eth3.csv')
    pd_data.plot()
    plt.show()

得到结果如下：

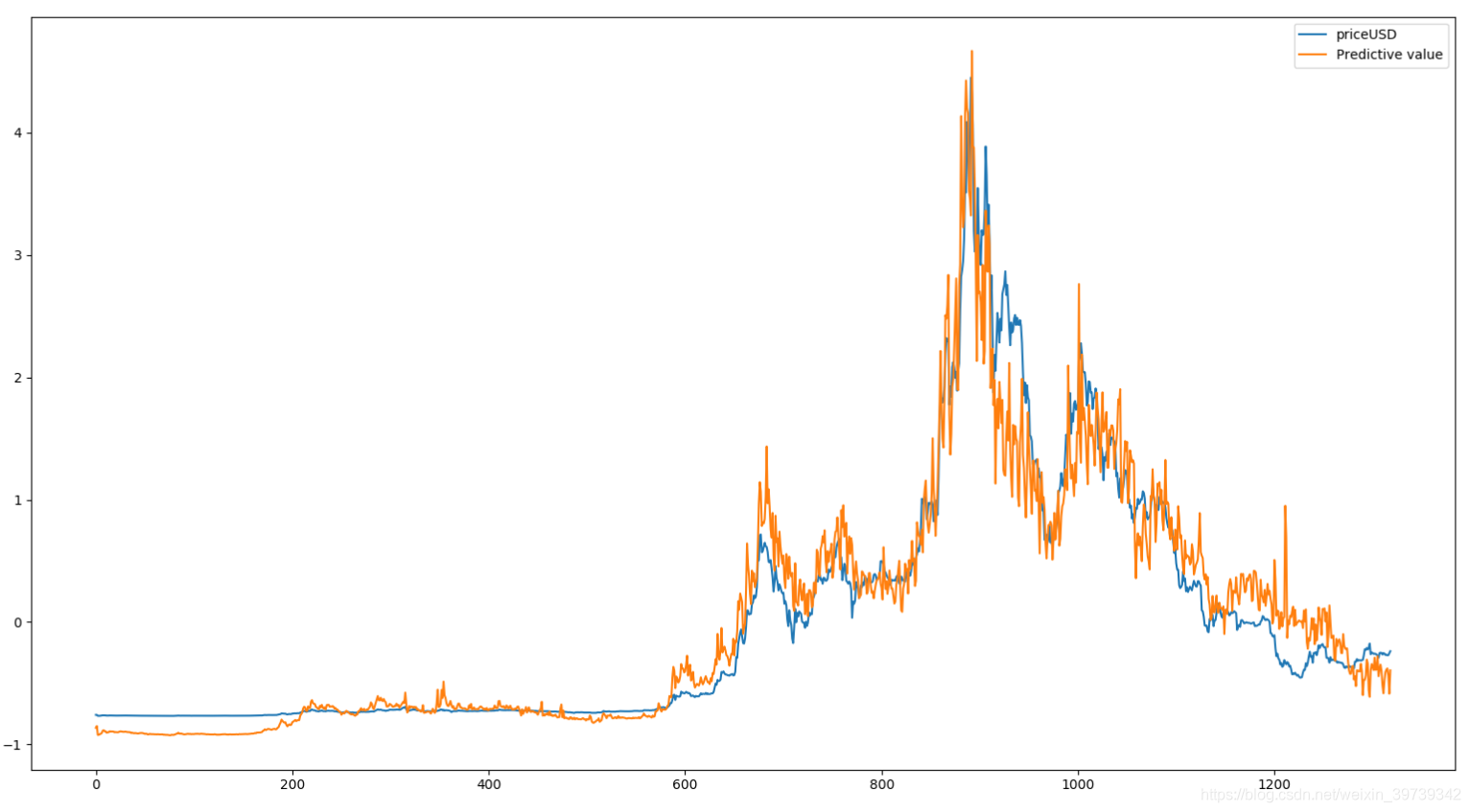
⑤数据及相关的py文件：https://download.youkuaiyun.com/download/weixin_39739342/11254555