数据结构(二十五) -- 常用的十种算法(七) -- Kruskal算法

1. 公交站问题

2. Kruskal算法介绍

1. Kruskal算法是用来求加权连通图的最小生成树的算法
2. 基本思想：按照权值从小到大的顺序选择n-1条边，并保证这n-1条边不构成回路
3. 具体做法：首先构造一个含有n个顶点的森林，然后依照权值从小到大从连通网中选择边加入到森林中，并使森林中不产生回路，直到森林变成一棵树为止

2.1 图解说明

以公交站问题来进行图解说明：

在含有n个顶点的连通图中选择n-1条边，构成一颗极小连通子图，并使该连通子图中n-1条边上权值之和达到最小，则称其为连通网的最小生成树。

例如，对于上图G4所示的联通网可以有多棵权值总和不同的生成树

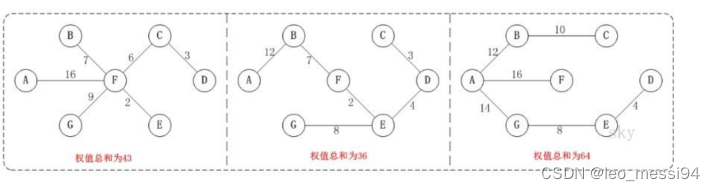
用上图G4，来对Kruskal进行演示：（用数组R保存最小生成树结果）

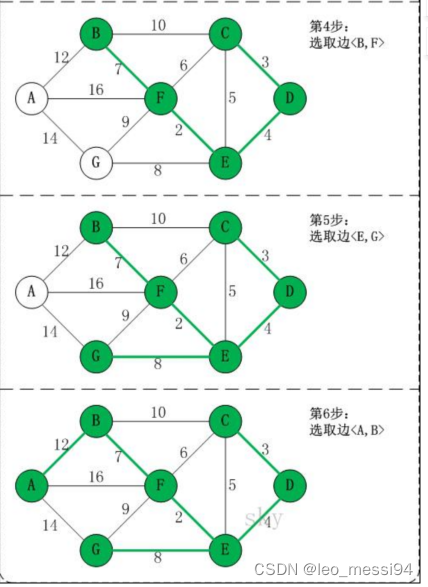
2.2 算法分析：

2.3 如何判断是否构成回路：

3. 代码完成公交车站问题：

public class KruskalCase {
   

	private int edgeNum; //边的个数
	private char[] vertexs; //顶点数组
	private int[][] matrix; //邻接矩阵
	//使用 INF 表示两个顶点不能连通
	private static final int INF = Integer.MAX_VALUE;

	public static void main(String[] args) {
   
		char[] vertexs = {
   'A', 'B', 'C', 'D', 'E', 'F', 'G'};
		//克鲁斯卡尔算法的邻接矩阵
		int matrix[][] = {
   
						/*A*//*B*//*C*//*D*//*E*//*F*//*G*/
				/*A*/ {
      0,  12, INF, INF, INF,  16,  14},
				/*B*/ {
     12,   0,  10, INF, INF,   7, INF},
				/*C*/ {
    INF,  10,   0,   3,   5,   6, INF},
				/*D*/ {
    INF, INF,   3,   0,   4, INF, INF},
				/*E*/ {
    INF, INF,   5