

package com.chb.Kruskal;
import java.util.Arrays;
public class KruskalCase {
private int edgeNum; //边的个数
private char[] vertexs; //顶点数组
private int[][] matrix; //邻接矩阵
//使用 INF 表示两个顶点不能连通
private static final int INF = Integer.MAX_VALUE;
public static void main(String[] args) {
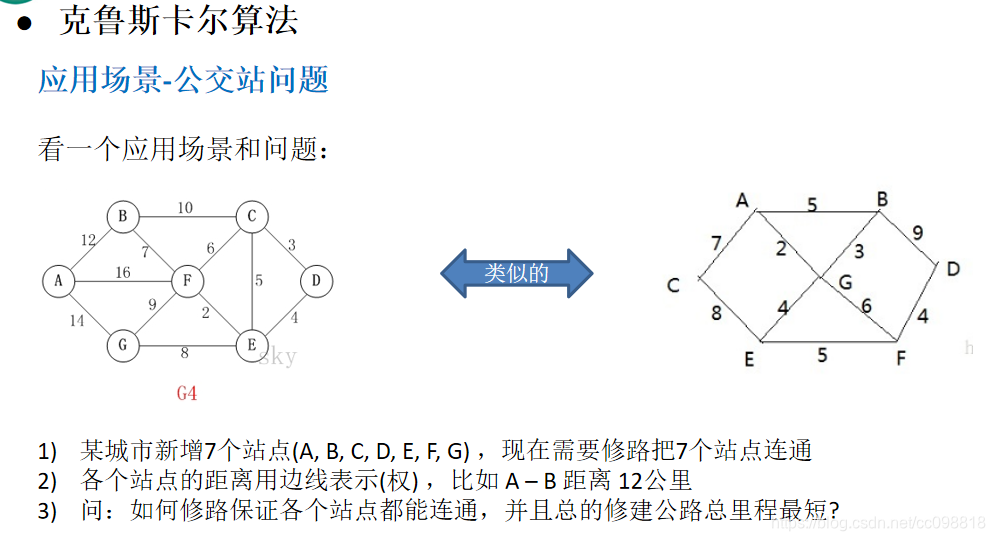
char[] vertexs = {
'A', 'B', 'C', 'D', 'E', 'F', 'G'};
//克鲁斯卡尔算法的邻接矩阵
int matrix[][] = {
/*A*//*B*//*C*//*D*//*E*//*F*//*G*/
/*A*/ {
0, 12, INF, INF, INF, 16, 14},
/*B*/ {
12, 0, 10, INF, INF, 7, INF},
/*C*/ {
INF, 10, 0, 3, 5, 6, INF},
/*D*/ {
INF, INF, 3, 0, 4, INF, INF},
/*E*/ {
INF, INF, 5, 4, 0, 2, 8},
/*F*/ {
16, 7, 6, INF, 2, 0, 9




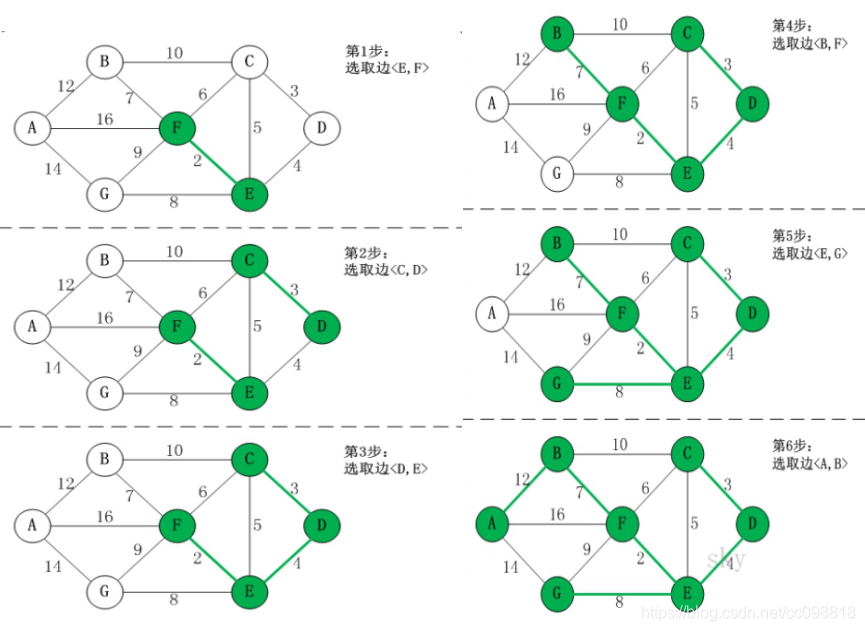
 本文深入探讨了Kruskal算法,一种用于解决最小生成树问题的经典图论算法。详细解释了算法步骤,包括边的排序、并查集的使用以及如何避免形成环。通过实例展示了Kruskal算法如何找到图中权重最小的边来构建树,同时讨论了其在图论和网络优化中的应用。
本文深入探讨了Kruskal算法,一种用于解决最小生成树问题的经典图论算法。详细解释了算法步骤,包括边的排序、并查集的使用以及如何避免形成环。通过实例展示了Kruskal算法如何找到图中权重最小的边来构建树,同时讨论了其在图论和网络优化中的应用。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








