前言:高阶导数对于一阶二阶导数来说更难一些,更富有技巧性,大多数情况下不允许你蛮干,有些常用的规律必须得记住,当然学会这些知识的前提,还是得把16个基本求导公式得背熟,背不熟做一步卡一步。
正文:
1.高阶导数的定义:
 函数
函数  的导数
的导数 仍是 x 的函数,通常把导函数
仍是 x 的函数,通常把导函数 的导数叫做函数的二阶导数,记作
的导数叫做函数的二阶导数,记作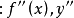
即 或者可以写成:
或者可以写成:
类似地,二阶导数的导数叫做三阶导数,三阶导数的导数叫做四阶导数…… . 一般地,n-1阶导数的导数叫做 n 阶导数,即
 分别记作
分别记作
或者写为 二阶及二阶以上的导数统称为高阶导数。 *该词条来自于百度百科
二阶及二阶以上的导数统称为高阶导数。 *该词条来自于百度百科
2.高阶导数运算方法
①归纳法(思想是逐次求导,找出规律得通式)
栗子1

它的一阶导数到n阶导数的式子如下

得出通式得

栗子2

栗子3

通过若干阶导数的计算可看出,sinx的高阶导数具有一种循环性,其循环规律涉及两个因素,一是总在sin x 和 cos x 之间交互转换,二是符号交互变化
由于涉及两个变化因素,使得确定导数规律相对困难,故考虑改写各阶导数形式,以减少其间变化因素,并使其和导数阶数发生联系
重要的高阶求导公式:


②用高阶导数求导公式

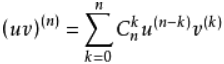 这个公式被称为莱布尼兹公式
这个公式被称为莱布尼兹公式
如果见到两个乘积的高阶导数,一般用莱布尼兹公式即可,同时要结合上述所给的公式来求解,若求一个高阶导数比较困难时,若能转化成两个函数乘积的形式,亦用莱布尼兹公式
栗子4

栗子5

栗子6

3.泰勒公式或麦克劳林公式,比较系数
如果 在点x=x0具有任意阶导数,则幂级数
在点x=x0具有任意阶导数,则幂级数

称为  在点x0处的泰勒级数在泰勒公式中
在点x0处的泰勒级数在泰勒公式中
取x0=0,得到的级数 称为麦克劳林级数
称为麦克劳林级数
常见的幂级数展开式
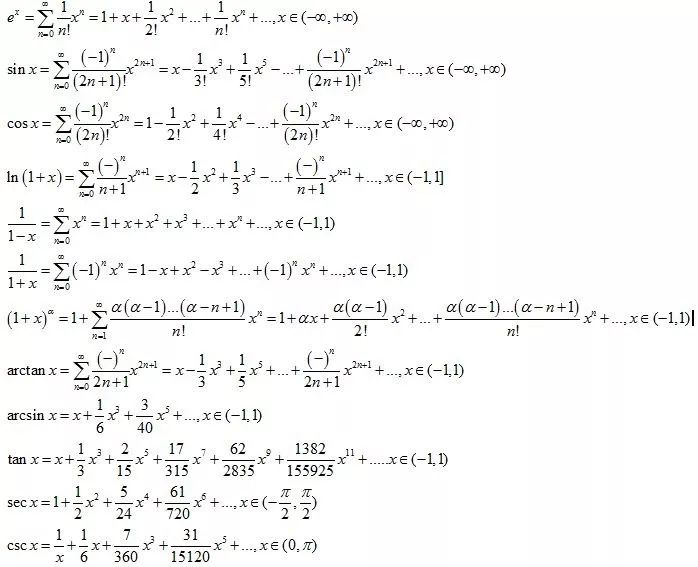
栗子7


对文章有什么疑问或错误,欢迎与我一起讨论
如果觉得文章还不错,点个打赏分享再走吧
笔耕不错,有你支持























 2158
2158

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








