c莫比乌斯函数_算法学习笔记(36): 莫比乌斯反演

最新推荐文章于 2024-05-22 22:25:33 发布

weixin_39585035

最新推荐文章于 2024-05-22 22:25:33 发布

阅读量128

点赞数

CC 4.0 BY-SA版权

文章标签： c莫比乌斯函数

本文链接：https://blog.youkuaiyun.com/weixin_39585035/article/details/112221117

这篇博客介绍了如何利用狄利克雷卷积和莫比乌斯反演解决数论问题，特别是它们在竞赛中的应用。文章详细阐述了莫比乌斯函数的计算方法，通过欧拉筛实现，并展示了如何通过提取公因数和整除分块技巧简化数学表达式。还提供了若干例题，如求特定条件下的二元组数量，进一步解释了这些技巧的实际运用。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

在学习了狄利克雷卷积后，莫比乌斯反演公式就是非常显然的了：

展开来写：

其实如果你掌握了狄利克雷卷积，你并不需要记忆这个公式，而且很多题目也不会直接用到它。

至于莫比乌斯函数的计算，可以利用欧拉筛在

时间内筛出（和筛欧拉函数类似）：

int mu[MAXN];
bool isnp[MAXN];
vector<int> primes;
void init(int n)
{
    mu[1] = 1;
    for (int i = 2; i <= n; i++)
    {
        if (!isnp[i])
            primes.push_back(i), mu[i] = -1; // 质数为-1
        for (int p : primes)
        {
            if (p * i > n)
                break;
            isnp[p * i] = 1;
            if (i % p == 0)
            {
                mu[p * i] = 0; // 有平方因数为0
                break;
            }
            else
                mu[p * i] = mu[p] * mu[i]; // 互质，利用积性函数性质
        }
    }
}

在竞赛中，莫比乌斯反演常常用在与

有关的题目上，且常常涉及到数论题中两个常用的小技巧：

提取公因数，整除分块。

提取公因数

设有

，根据上篇笔记的经验，连续的求和式可以替换成等价的形式。而这里三个求和号的约束条件分别是

。于是我们转而枚举

，发现

，且对于每个

，都有

. 所以令

，则

，在

上相当于

. 所以：

（注意：需要把原函数转化成关于

的函数

）

如果你看着公式推导觉得比较绕，我画了一张图帮助理解：

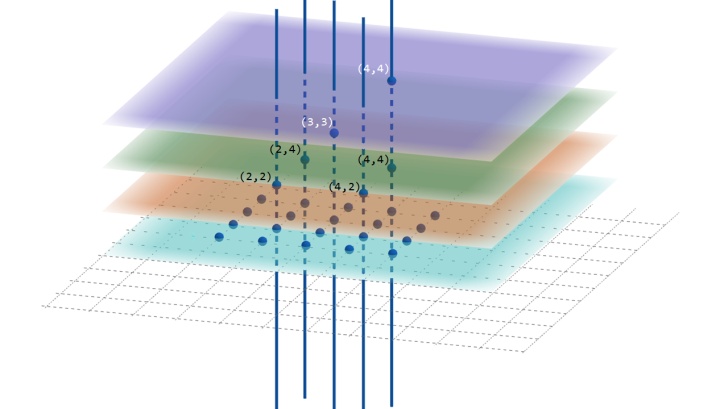
z轴代表

，可以发现

时就是1个1个一组，

时就是2个2个一组……等等。

这个公式还可以推广，比如只有两个求和号的情形：

四个求和号的情形：

（

）

等。

整除分块

（其实我和我的队友 @朝夕曾经独立发明了这个算法……）

假如我们要求

，朴素地求肯定是

的，但是我们打表会发现，有大量的连续项具有相同的值：

⌊60/i⌋的取值分布

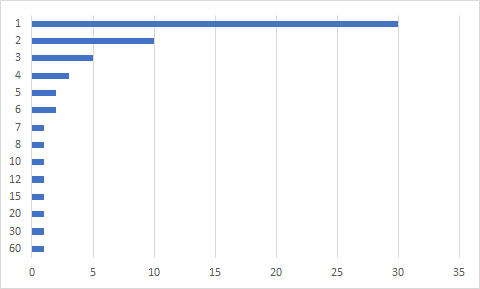
所以我们可以把相同的项一起计算。现在的问题是如何找到这些段。我们可以证明，设每一段的左端点为

，则右端点为

：

设

，则

，故

，由于

是整数，所以

的最大值为

。

这样就可以写出整除分块的代码：

for (int l = 1, r; l <= n; l = r + 1)
{
    r = n / (n / l);
    ans += (r - l + 1) * (n / l);
}

很容易证明总段数不超过

（以除数为

为分界线讨论即可），所以整除分块时间复杂度为

这也可以用来计算因数个数函数

的前缀和，因为：

来看一下例题：

求
且
的二元组数量。

定义

，现在我们求

。

显然，

，所以原式=

，根据

，有原式=

。这个式子是不是非常熟悉？直接

提取公因数得到：

后面这一块可以用整除分块计算。先预处理出

的前缀和

sum。同时对两个整除式进行分块，每次取步长较短的一段：

for (int l = 1, r; l <= min(n, m); l = r + 1)
{
    r = min(n / (n / l), m / (m / l));
    ans += (sum[r] - sum[l - 1]) * (n / l) * (m / l);
}

稍微把题目变形一下：

求
且
的二元组数量。

现在要求的是

，直接令

，可以得到

，然后就和刚刚一样了，把

替换成

即可。

再比如说：

求
的值.

好吧，这个题其实跟莫比乌斯函数没什么关系，但也可以用狄利克雷卷积+提取公因数+整除分块化简，本质上差不多。

洛谷P2398的数据较小，可以用复杂度较大的方法解决。但复杂度更优的方法是预处理出

的前缀和，然后整除分块求解即可。

一般地，如果

可以预处理出前缀和

sum，则

的求法为：

for (int l = 1, r; l <= min(n, m); l = r + 1)
{
    r = min(n / (n / l), m / (m / l));
    ans += (sum[r] - sum[l - 1]) * (n / l) * (m / l);
}

这种题目，难度主要在于推式子，而且一般不是可以打表看出来的，所以需要把各种数论定理牢记于心。当然，这一块还有很多技巧，这里暂不介绍了。

Pecco：算法学习笔记（目录）zhuanlan.zhihu.com